Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to DFT
Unlock Audio Lesson
Today we will discuss the Discrete Fourier Transform, or DFT. Can anyone tell me what Fourier Transform does?
It converts a signal from the time domain to the frequency domain?
Exactly! The DFT specifically handles discrete signals or samples. So, what do we mean by 'discrete'?
I think it means that the signal is captured at specific time intervals.
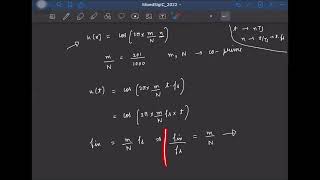
Correct! Now, remember the DFT formula \( F(k) = \sum_{n=0}^{N-1} f_n e^{-2\pi i k n/N} \). The number of samples is \( N \) and \( k \) is the index for the frequency component. This transformation allows us to find the dominant frequencies in our sampled signals.
How is this useful in real applications?
Great question! It's widely used in signal processing. Let’s keep that in mind as we explore its applications.
Fast Fourier Transform (FFT)
Unlock Audio Lesson
Now that we know about DFT, let’s talk about the Fast Fourier Transform, or FFT. Does anyone know how it differs from DFT?
I've heard it’s faster but not exactly how.
That’s right! The FFT significantly reduces the number of computations needed for DFT, going from \( O(N^2) \) to \( O(N \log N) \). This efficiency makes it suitable for real-time applications.
Can you give an example where FFT is used?
Certainly! It’s extensively used in structural health monitoring to process the data from sensors quickly. Understanding frequencies helps in assessing the structure's response to vibrations.
Applications of DFT in Civil Engineering
Unlock Audio Lesson
Let’s explore how DFT and FFT are used in civil engineering. What do you think is one of the primary applications?
Maybe in analyzing vibrations in buildings?
Absolutely! Vibration analysis helps in modal analysis for structures. By examining frequency responses, engineers can evaluate how structures will behave under dynamic loads.
Are there any other applications?
Yes! FFT is also crucial in dynamic soil testing and assessing resonance in concrete structures, which can prevent potential failures.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The DFT transforms a finite sequence of time-domain samples into their frequency-domain representation, facilitating analysis of signals that have been digitized through sampling. This process is implemented efficiently using the Fast Fourier Transform (FFT) algorithm, widely utilized in applications such as structural health monitoring.
Detailed
Detailed Summary
The Discrete Fourier Transform (DFT) is a transformation used to analyze discrete signals that are captured in a sampled format—essentially breaking these signals down into their constituent frequencies. For a finite sequence of samples represented as \( f_0, f_1, ..., f_{N-1} \), the DFT is computed as:
\[
F(k) = \sum_{n=0}^{N-1} f_n e^{-2\pi i k n/N}, \quad k=0, 1, \dots, N-1
\]
This formula translates time-domain information to the frequency domain, helping engineers and scientists understand and manipulate digital signals. Conversely, to reconstruct the original time domain signal from its DFT, we apply the inverse DFT:
\[
f_n = \frac{1}{N} \sum_{k=0}^{N-1} F(k) e^{2\pi i k n/N}
\]
To compute the DFT efficiently, the Fast Fourier Transform (FFT) algorithm is employed, which reduces the computational complexity significantly, making it feasible for real-time applications and analyses, especially in fields like civil engineering where time-sensitive data is crucial.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Discrete Fourier Transform
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In real-world applications (such as sensor data in structural health monitoring), signals are sampled. The Discrete Fourier Transform (DFT) is used to analyze such sampled signals.
Detailed Explanation
The Discrete Fourier Transform (DFT) is a method used to convert a sequence of sampled signals into their frequency components. This is essential because in practical applications, we often deal with digital signals that are sampled at discrete time intervals rather than continuous signals. The DFT helps us to analyze these sampled sequences by transforming them from the time domain into the frequency domain, allowing us to study their frequency characteristics.
Examples & Analogies
Imagine you're trying to understand the musical notes of a song that has been recorded. Each note is played for a short moment, and the recording captures discrete sound samples. The DFT will take these samples and break down the song into its component notes (frequencies), enabling you to see which notes are present and how loud each one is.
Definition of DFT
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a finite sequence f_0, f_1, ..., f_{N−1}, the DFT is:
N−1
X
F_k = f_n e^{-2πikn/N}, k = 0, 1, ..., N − 1
n=0
Detailed Explanation
The formula for the Discrete Fourier Transform specifies that each output frequency component, denoted as F_k, is calculated by summing (adding together) the products of the sample values f_n with complex exponentials. The variable k indicates which frequency component you are calculating, while n indexes each sample in the sequence. The term e^{-2πikn/N} represents a rotating wave, which helps in mapping the time-domain signal to its frequency-domain representation.
Examples & Analogies
Think of the DFT like a chef making a salad. Each ingredient (sample value) is added to the mix in a specific way (multiplied by the complex exponential), and the final dish (F_k) is the unique mix of flavors (frequency components) that result from combining these ingredients in the right amounts.
Inverse DFT
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Inverse DFT:
1/N
X
f_n = F_k e^{2πikn/N}
N k=0
Detailed Explanation
The Inverse Discrete Fourier Transform (IDFT) allows us to reconstruct the original signal from its frequency components (F_k). This formula shows that each sample in the original time-domain signal, f_n, can be recreated by summing the contributions of all frequency components, each multiplied by a complex exponential. Just like the DFT, this process goes through all frequency components but reverses the calculation to come back to the original time-domain signal.
Examples & Analogies
Consider a recipe that uses multiple ingredients to create a smoothie. If you blend all the ingredients together (DFT), you get a tasty smoothie (frequency domain representation). However, if you take that smoothie and want to identify its components (inverse operation), you need to 'unblend' it, which can be compared to the process of the Inverse DFT to find the original ingredients (samples).
Efficiency Through FFT
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is implemented efficiently using the Fast Fourier Transform (FFT) algorithm.
Detailed Explanation
The Fast Fourier Transform (FFT) is an advanced algorithm that computes the DFT much faster than the straightforward computation. While the DFT involves a lot of repeated calculations—resulting in higher computational complexity—the FFT reduces this to a much more manageable level, making it feasible to analyze large datasets or signals in real-time applications.
Examples & Analogies
Imagine you have to organize a massive library of books. If you do it manually, it can take a lot of time. However, using an efficient cataloging system (like the FFT), you can quickly sort through the books and find everything you need without going through each book individually. This time-saving approach is vital in applications like structural health monitoring where timely data analysis is critical.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Discrete Sampling: The process of capturing a signal at distinct time intervals.
-
DFT Formula: \( F(k) = \sum_{n=0}^{N-1} f_n e^{-2\pi i k n/N} \) describes the transformation.
-
Inverse DFT: Allows reconstruction of the original signal from its frequency components.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Analyzing the frequency components of sensor data from a bridge to ensure structural integrity.
-
Using FFT to process live data from accelerometers during earthquake monitoring.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
FFT, oh so fast, DFT's calculations couldn't last.
📖 Fascinating Stories
-
Imagine a baker sampling every hour to ensure the bread is just right - that's like DFT measuring signals at specific times.
🧠 Other Memory Gems
-
F-D-FFT stands for Frequency-Domain Fast Fourier Transform.
🎯 Super Acronyms
DFT - Discrete Frequency Transformation
- Remembering the method of changing data.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Discrete Fourier Transform (DFT)
Definition:
A mathematical technique to convert a finite sequence of time-domain samples into a frequency-domain representation.
-
Term: Fast Fourier Transform (FFT)
Definition:
An efficient algorithm for computing the Discrete Fourier Transform, reducing computational time.
-
Term: Frequency Domain
Definition:
A representation of signals based on their frequency components rather than their time representation.
-
Term: Signal Processing
Definition:
The analysis, interpretation, and manipulation of signals.