Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Basis and Representation
Unlock Audio Lesson
Alright class, let's discuss how every vector can be represented in terms of a chosen basis. What do you all think a basis represents in a vector space?
I think it's like the building blocks for vectors, right? Each vector is made up of these blocks.
Exactly! In a vector space, a basis is a set of vectors that can be combined in various ways to create any vector in that space. For example, if we have a basis B consisting of vectors b₁, b₂, ..., bₙ, we can express a vector v as a linear combination of these basis vectors.
So, basically if we have v = a₁b₁ + a₂b₂ + ... + aₙbₙ, then a₁, a₂, ..., aₙ are the coordinates of v relative to basis B?
Correct! And these coefficients—our coordinates—allow us to uniquely identify each vector in the space. Remember: **B** is the 'Building' set. This will help you remember that every vector is built from these basis vectors.
Can these basis vectors be changed? Like, what if I want to use a different set?
Great question! This leads us into the concept of changing basis, which allows us to express the same vector in different contexts. Let's dive into that next.
Change of Basis
Unlock Audio Lesson
Now that we understand what a basis is, let's discuss changing the basis for a vector. If you already have a vector with coordinates in basis B, how do you represent it in basis C?
Wouldn't we need a transformation matrix?
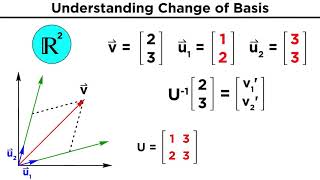
Spot on! We use a matrix P whose columns are the coordinates of the basis vectors of B as expressed in C. When we have [v]_B for a vector v, we can find [v]_C using the formula [v]_C = P⁻¹·[v]_B.
So, how do we find P? Is it just showing how each basis vector in B relates to the ones in C?
Exactly! Each entry in P shows you how to convert between the coordinates of bases. This process is crucial in applications, such as in structural analysis where various reference frames are involved.
Could you give us an example of how this applies in Civil Engineering?
Of course! In finite element methods, engineers often need to interpret results from one frame of reference to another for accurate analysis and calculations. This change of basis allows for such transformations to make sense of complex structures.
This sounds important; using the right basis can change everything!
Absolutely! Remember, transitioning between bases enables clarity in complex analyses.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore how every vector can be uniquely represented relative to a chosen basis and how to convert those coordinates when transitioning between different bases. This concept is pivotal in many applications, especially within Civil Engineering.
Detailed
Coordinate Systems and Change of Basis
Given a basis B composed of vectors {b₁, b₂, ..., bₙ} for a vector space V, any vector v in V can be expressed uniquely as a linear combination of those basis vectors:
v = a₁b₁ + a₂b₂ + ... + aₙbₙ,
where the scalars a₁, ..., aₙ are known as the coordinates of v relative to the basis B.
Change of Basis
When a vector has coordinates [v]_B in basis B and [v]_C in a different basis C, we can transform the coordinates between these bases using the relation:
[v]_C = P⁻¹·[v]_B,
where P is the matrix whose columns contain the coordinates of the basis vectors of B relative to basis C. This process is crucial in fields like Civil Engineering, where it applies to changing reference frames in structural analysis and interpreting results in finite element analysis (FEM). Thus, understanding the principles of basis and vector representation enables engineers to manipulate and visualize complex problems effectively.
Youtube Videos
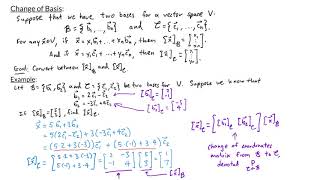
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Representation of Vectors in a Basis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Given a basis B = {b₁, b₂, ..., bₙ} for V, every vector v ∈ V can be uniquely represented as: v = a₁b₁ + a₂b₂ + ... + aₙbₙ
The scalars a₁, ..., aₙ are the coordinates of v relative to B.
Detailed Explanation
In linear algebra, any vector within a vector space can be expressed in terms of a basis. A basis is a set of vectors that are linearly independent and span the vector space. When we say that a vector v can be uniquely represented as a combination of basis vectors b₁, b₂, ..., bₙ, we mean we can break down the vector v into parts that point in the same direction as each of these basis vectors. The scalars a₁, a₂, ..., aₙ that multiply these basis vectors are called the coordinates of the vector v relative to the basis B. This unique representation is crucial because it allows us to analyze and manipulate vectors using the structure provided by the basis.
Examples & Analogies
Think of a vector as a recipe for a smoothie, where the basis vectors (b₁, b₂, b₃) are the different fruits you can use. The coefficients (a₁, a₂, a₃) indicate how much of each fruit you need in the smoothie. Just like with the right ingredients, you can create a delicious final product that is unique to a specific mix of those fruits; in the same way, each vector's unique combination of basis components allows it to occupy a specific location in vector space.
Change of Basis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Change of Basis: If a vector has coordinates [v]_B in basis B and [v]_C in basis C, then [v]_C = P⁻¹·[v]_B
Where P is the matrix whose columns are the coordinates of B in terms of C.
Detailed Explanation
Changing the basis of a vector involves translating its coordinates from one basis to another. If you have a vector represented in basis B as [v]_B, and you want to find out its expression in another basis C, you need a transformation matrix P. This matrix P contains information about how the basis B is represented in terms of the new basis C. The equation [v]_C = P⁻¹·[v]_B shows that to convert the coordinates back to basis C, we multiply by the inverse of the basis change matrix. This change of basis is fundamental in applications like computer graphics, where the orientation of objects is frequently switched between different reference frames.
Examples & Analogies
Imagine you are using two different languages to describe the same location on a map. When you say '10 kilometers north' in one language, the equivalent phrase in another language might be '10 kilometers to the top.' To translate between these descriptions, you would need to know how to convert expressions from one language to another, much like how the matrix P converts coordinates from one basis to another in our vector space.
Applications in Civil Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This has significant applications in Civil Engineering, such as:
- Changing reference frames in structural analysis
- Interpreting results from global to local element coordinates in FEM
Detailed Explanation
The process of changing coordinate systems and understanding basis transformations is incredibly useful in Civil Engineering. For example, in structural analysis, engineers often need to consider how forces and displacements act in different coordinate frames, especially when a structure is being viewed from different perspectives. Additionally, when using the Finite Element Method (FEM), engineers need to interpret the global coordinates of their model into local coordinates that correspond to specific elements, which greatly helps in analyzing and optimizing each part of the structure.
Examples & Analogies
Think of it as adjusting your view when watching a sports game from different angles. Depending on where you sit in the stadium—whether you're at the center or off to the side—the strategy to understand the plays on the field changes, as does your perspective on who's winning. In the same way, engineers adjust their coordinate systems based on what part of the structure they are examining, ensuring they have the clearest understanding of how forces are distributed throughout the entire system.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Basis: A set of vectors that uniquely spans a vector space.
-
Coordinates: Numeric values representing the vector's position in relation to a basis.
-
Change of Basis: The method for transitioning from one basis representation to another, using transformation matrices.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of expressing vector v = (3, 4) in new basis vectors like b₁ = (1, 0) and b₂ = (0, 1).
-
Illustration of changing the coordinate representation of a vector from basis B to basis C using the transformation matrix P.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To change the basis, don't be in a haze; P⁻¹'s the key to see your way.
📖 Fascinating Stories
-
Imagine a traveler moving between two countries, each with its own numerical language. To communicate effectively, the traveler carries a translation book (the transformation matrix P), allowing them to express themselves clearly in any language.
🧠 Other Memory Gems
-
B.C.C.: Basis to Coordinates to Change - remember the sequence in handling vector transformations.
🎯 Super Acronyms
BASIS
- Building All Spatial Interconnections Sustainably.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Basis
Definition:
A set of vectors that defines a vector space, allowing every vector in that space to be expressed as a linear combination of those vectors.
-
Term: Change of Basis
Definition:
The process of converting the coordinates of a vector when transitioning from one basis to another.
-
Term: Coordinates
Definition:
Numerical values that define a vector's position in relation to a given basis.
-
Term: Transformation Matrix
Definition:
A matrix that contains the coefficients needed to convert coordinates of vectors between different bases.