Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Basics of Isomorphism
Unlock Audio Lesson
Today we're discussing vector space isomorphism. Let's start with the definition: two vector spaces are isomorphic if there's a bijective linear transformation between them that respects vector addition and scalar multiplication.
What does 'bijective' mean in this context?
Great question! 'Bijective' means the transformation matches every element in one space to exactly one element in the other space and vice versa. This property ensures a one-to-one correspondence.
Does this imply that the dimensions of both spaces are the same?
Yes! If two vector spaces are isomorphic, their dimensions will be equal. This is a key feature as it tells us the two spaces are structurally similar.
Significance of Isomorphism
Unlock Audio Lesson
So why is understanding isomorphism important? By proving two spaces are isomorphic, you can apply concepts and methods from one space in another.
Can you give an example where this is useful?
Sure! In engineering, transforming systems of equations from one form to another can be easier by recognizing that different representations are isomorphic.
What happens if two spaces aren't isomorphic?
If they aren't isomorphic, they have different dimensions or structure, meaning you cannot directly apply results from one to the other without additional work.
Examples of Isomorphic Spaces
Unlock Audio Lesson
Let's look at some practical examples of isomorphic vector spaces. For instance, the space of 2D real vectors ℝ² and the plane of polynomials of degree at most 1 are isomorphic.
How can they be isomorphic if they seem very different?
It's their structure that's the same—each can be manipulated in the same ways, adhering to the same rules. In both, you can represent points and lines equivalently.
If they are isomorphic, does that mean solutions in one can be translated into the other?
Exactly! Solutions or operations in one space can be effectively mirrored in the other, facilitating easier problem-solving.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Isomorphic vector spaces V and W have the same dimension and allow for a one-to-one correspondence through a linear transformation that maintains the structure of the vector spaces, thereby allowing operations such as vector addition and scalar multiplication to be carried over between them without loss of information.
Detailed
Vector Space Isomorphism
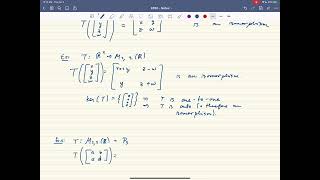
Vector space isomorphism establishes a critical relationship between two vector spaces, denoted as V and W. Specifically, these spaces are considered isomorphic if there exists a bijective linear transformation (denoted as T: V → W) that preserves vector addition and scalar multiplication.
An important consequence of this definition is that if two vector spaces are isomorphic, they possess the same dimension; thus, if dim(V) = dim(W), we can write V ≅ W. This concept is crucial in many applications, including those in engineering, where the structure of vector spaces helps in solving complex problems involving abstract representations of physical quantities.
Understanding isomorphism enables engineers and mathematicians to transfer knowledge and techniques between different contexts, thereby expanding their approaches to problem-solving.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Dimension and Isomorphism
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If dim(V) = dim(W), then V ≅ W.
Detailed Explanation
This part of the section highlights an important condition for vector space isomorphism, which is the equality of dimensions. The dimension of a vector space is the number of vectors in a basis for that space, indicating how 'large' or 'complex' the vector space is. If two vector spaces have the same dimension, it is a necessary condition for them to be isomorphic. However, having the same dimension alone does not guarantee isomorphism, as the actual structure and relationships between elements must also match through a bijective linear transformation. Thus, if we find that dim(V) equals dim(W), it opens up the possibility that these spaces might be isomorphic, which is an essential concept when we're analyzing their relationships in applied mathematics and engineering.
Examples & Analogies
Think of two classrooms, one for kids learning music and the other for kids learning painting. If both classrooms have the same number of students (say 20 kids), we can say that they have the same 'dimension' in terms of student count. However, the experience of learning music is as different from painting as the two vector spaces might differ overall. Despite having the same number of students, we can only consider how well they can share lessons and ideas by establishing a comparison of content, making the search for true isomorphism important—in this case, ensuring both lessons can transform similarly using their unique skills.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Isomorphic Vector Spaces: Two vector spaces that have a bijective linear transformation allowing similar operational results.
-
Dimension: A measure of the number of vectors in the basis of a vector space, crucial in determining isomorphism.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of isomorphic spaces includes the space of real 2D vectors and the polynomial space of degree 1. Both have identical dimensionality and can perform similar operations.
-
The vector space of 3D vectors and the space of real-valued continuous functions defined on a compact interval can also be isomorphic under specific linear transformations.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To find if they're isomorphic, check the space's flow,/
📖 Fascinating Stories
-
Imagine two teams working on a project. They can share ideas if they have the same skills (dimensions) and communicate clearly (isomorphism). When they are in sync, they achieve great results together!
🧠 Other Memory Gems
-
For isomorphism remember: B for bijective connections and D for dimensions being equal.
🎯 Super Acronyms
ISOMORPH
- Isomorphic Spaces Operate Mechanically on Respective Properties Harmoniously.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Isomorphism
Definition:
A bijective linear transformation that connects two vector spaces while preserving their operations.
-
Term: Bijective
Definition:
A property of a function that means it is both injective (one-to-one) and surjective (onto).
-
Term: Linear Transformation
Definition:
A function between two vector spaces that preserves the operations of vector addition and scalar multiplication.