Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Euclidean Space
Unlock Audio Lesson
Today, we will explore one of the most fundamental examples of vector spaces: Euclidean space, denoted as ℝⁿ. Can anyone tell me what this notation implies about the space we're discussing?
It represents the set of n-tuples of real numbers!
Exactly! In more simple words, it's like having a space where each vector has n components, all being real numbers. So in Euclidean space, we can perform vector addition and scalar multiplication. Can you remind me what these operations involve?
Vector addition involves combining two vectors to create a new vector, and scalar multiplication is scaling a vector by a number.
Imagine we are working in ℝ², like a 2D plane. You can visualize it like plotting a point with two coordinates.
So each vector can be represented as a point in this plane?
Correct! And what about more dimensions? How do we visualize ℝ³?
It would be represented in a 3D space, adding depth!
Absolutely! So, can someone summarize what we've discussed about ℝⁿ?
It's a vector space of n-tuples of real numbers with defined operations.
Set of Polynomials
Unlock Audio Lesson
Let's move on to another interesting vector space: the set of polynomials denoted Pₙ. What do you think this includes?
It includes all polynomials of degree less than or equal to n with real coefficients?
That's right! Polynomials can be expressed as a linear combination of their terms. For example, a polynomial p(x) = a₀ + a₁x + a₂x² ... aₙxⁿ lies within this space. How do you think we can perform operations like addition or scalar multiplication on polynomials?
We can add the coefficients together or multiply the polynomial by a scalar!
Excellent! This space allows us to model many physical situations through the behavior of polynomials. Can anyone think of real-life applications where polynomials are useful?
Polynomial regression in data fitting or modeling curves!
That's a fantastic example! To remember Polynomials, utilize the mnemonic 'PAR' for Polynomial Addition and Representation. Let's recap: What is Pₙ?
It's the space of polynomials of degree n or fewer with real coefficients!
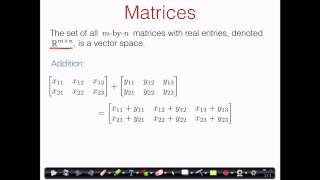
Matrix Spaces
Unlock Audio Lesson
Moving on, let’s look at the matrix space, denoted Mₘₓₙ(ℝ). What do you think it entails?
It includes all m×n matrices with real entries!
Yes! And when we perform operations on matrices such as addition or multiplication by a scalar, we're essentially working within a vector space. Why are matrix spaces particularly important in engineering?
They are used in solving systems of linear equations and transformations!
Correct! Remember the acronym 'SAR' for Scalar Addition and Representation when dealing with matrices. What properties can you state about the matrix space?
It is closed under addition and scalar multiplication, and it contains the zero matrix!
Fantastic! To summarize, matrix spaces allow various operations essential in calculations and engineering solutions. Can someone summarize Mₘₓₙ(ℝ)?
The space of all m×n matrices over ℝ with defined operations!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, several examples of vector spaces are detailed, including Euclidean space, polynomial spaces, matrix spaces, and others. Understanding these examples helps clarify how different mathematical constructs can fit within the framework of vector spaces, which is foundational in various applications, especially in engineering.
Detailed
Examples of Vector Spaces
This section explores specific examples of vector spaces, each providing insight into the diverse applications and structures that can be described as vector spaces. Understanding these examples is crucial for students, as they serve as a bridge between abstract theory and practical applications.
1. Euclidean Space ℝⁿ
Euclidean space is defined as the set of all n-tuples of real numbers, denoted V = ℝⁿ = {(x₁, x₂, ..., xₙ) | xᵢ ∈ ℝ}, where the standard operations of addition and scalar multiplication apply. This example encapsulates the geometric aspects of vector spaces, helping students visualize vectors in higher dimensions.
2. Set of Polynomials Pₙ
This vector space consists of all polynomials of degree less or equal to n with real coefficients. It showcases how abstract algebraic constructs can be represented as vector spaces, emphasizing the linear combination of polynomial terms.
3. Matrix Space Mₘₓₙ(ℝ)
The set of all m×n matrices forms a vector space over ℝ. This example is significant in linear algebra, particularly in applications related to systems of equations and transformations, serving as a practical illustration for engineering students.
4. Function Space
The space of all real-valued continuous functions defined on an interval [a, b] forms a vector space. This represents an essential class of vector spaces that find utility in various fields, including engineering and physics, where functions represent various phenomena.
5. Zero Vector Space
The trivial vector space {0} is a necessary inclusion to understand vector spaces fundamentally, illustrating the simplest case where vector operations yield only the zero vector, reinforcing closure properties.
In summary, these examples not only embody the definitions and operations of vector spaces but also provide students with real-world connections, particularly in Civil Engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Euclidean Space ℝⁿ
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- ℝⁿ (Euclidean Space): The set of all n-tuples of real numbers, V = ℝⁿ = {(x₁, x₂, ..., xₙ) | xᵢ ∈ ℝ}, with usual addition and scalar multiplication.
Detailed Explanation
The Euclidean space ℝⁿ consists of all possible vectors represented as n-tuples where each element is a real number. These vectors can be added together using vector addition, where the corresponding components are summed. Additionally, any vector in ℝⁿ can be stretched or shrunk by multiplying it with a scalar (a real number), creating another valid vector in the same space.
Examples & Analogies
Imagine a point in a 3D room where the coordinates define its position: (x, y, z). This point can be adjusted by combining it with other points (vector addition) or moving it farther away from the origin by stretching it (scalar multiplication). Just like points on a map represent locations in a city, vectors in ℝⁿ represent locations in multidimensional space.
Set of Polynomials
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Set of Polynomials: Pₙ = set of all polynomials of degree ≤ n with real coefficients.
Detailed Explanation
The set of polynomials of degree less than or equal to n includes expressions like a₀ + a₁x + a₂x² + ... + aₙxⁿ, where the coefficients a₀, a₁, ..., aₙ are real numbers. This set is a vector space because you can add two polynomials (resulting in another polynomial within the same degree) and multiply a polynomial by a scalar (which also results in a polynomial of the same or lower degree).
Examples & Analogies
Think of polynomials as recipes. Each polynomial is a recipe that combines real-number ingredients (coefficients) with different powers of x representing amounts of each ingredient. If you mix two recipes together (add polynomials), you create a new recipe still within the same family of dishes (the same degree). If you double a recipe (scalar multiplication), you still have a valid recipe.
Matrix Space
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Matrix Space: The set of all m×n real matrices: Mₘₓₙ(ℝ) is a vector space over ℝ.
Detailed Explanation
The set of all real m×n matrices forms a vector space because you can perform addition and scalar multiplication on matrices. When two matrices of the same size are added, their corresponding elements are added together to produce another matrix of the same size. Additionally, multiplying any matrix by a real number scales every element of the matrix, resulting in another matrix of the same size.
Examples & Analogies
Imagine a board with different colored squares. Each m×n matrix can be thought of as a layout of colored squares where each square represents a real number. When you want to add two layouts together, you simply combine the colors of the same squares. If you want to create a larger layout by intensifying the colors (scalar multiplication), you do so while keeping the overall structure of the layout.
Function Space
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Function Space: The set of all real-valued continuous functions defined on an interval [a, b].
Detailed Explanation
This space consists of all functions that map real numbers from the interval [a, b] to real numbers and are continuous. These functions can be added together and multiplied by scalars while maintaining continuity. Thus, any linear combination of such functions will also yield a continuous function within the same space.
Examples & Analogies
Think of functions as different paths on a graph. Each path can represent a journey across a landscape, and by adding two paths together, you create a new combined journey. If you were to speed up your journey (scalar multiplication), you would still have a valid path. This helps us visualize problems in physics and engineering, where smooth transitions are crucial.
Zero Vector Space
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Zero Vector Space: The set {0} is a trivial vector space.
Detailed Explanation
The zero vector space contains only the single vector known as the zero vector (0). It satisfies all axioms of a vector space, as you can add the zero vector to itself or multiply it by any scalar, and the results are still in the set. This space is important as it serves as the smallest vector space and is a foundational component in the study of vector spaces.
Examples & Analogies
You can think of the zero vector space like an empty room that contains no furniture. Even though there’s nothing there, it still exists. If you were to try to add anything into the room, it remains empty—like the zero vector. This concept is vital in mathematics as it helps us understand limits and foundational structures.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Euclidean Space: A vector space of n-tuples of real numbers, denoted as ℝⁿ.
-
Set of Polynomials: Vector space formed by polynomials of degree ≤ n with real coefficients.
-
Matrix Space: The space of all m×n real matrices, which is essential in linear algebra.
-
Function Space: A collection of real-valued continuous functions defined over an interval.
-
Zero Vector Space: The trivial case of a vector space containing only the zero vector.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Consider ℝ² as the space of points (x, y) where x and y are real numbers, and vector operations are defined geometrically.
-
The polynomial p(x) = 3 + 2x - x² belongs to P₂, representing the space of polynomials with degree 2.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In space where dimensions are n, real numbers are found again and again!
📖 Fascinating Stories
-
Imagine a group of friends, each with their own unique coordinate points. Together they create a beautiful map of possibilities in ℝ², showcasing their friendships in multiple dimensions!
🧠 Other Memory Gems
-
Use the acronym 'PAP' for Polynomials: Addition, and Polynomial terms.
🎯 Super Acronyms
Remember 'MAT' for Matrix spaces - Additive property, Transformation capability!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Euclidean Space
Definition:
The vector space of n-tuples of real numbers, denoted as ℝⁿ, equipped with standard operations of addition and scalar multiplication.
-
Term: Set of Polynomials
Definition:
The vector space consisting of all polynomials of degree less than or equal to n with real coefficients.
-
Term: Matrix Space
Definition:
The set of all m×n real matrices forming a vector space over ℝ.
-
Term: Function Space
Definition:
The set of all real-valued continuous functions defined on an interval [a, b], forming a vector space.
-
Term: Zero Vector Space
Definition:
The trivial vector space consisting of only the zero vector.