Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Orthogonality
Unlock Audio Lesson
Today, we are going to discuss orthogonality. Two vectors u and v are orthogonal if their inner product is zero, meaning they are at right angles to each other. Can anyone tell me what that looks like geometrically?
So, it’s like when two lines meet at a 90-degree angle, right?
Exactly! And why do you think orthogonality is important in engineering?
It might help to simplify problems, especially when working with forces or vectors.
That's spot on! Orthogonal vectors can help with easier calculations. Now, let’s transition into understanding orthonormal sets.
Understanding Orthonormal Sets
Unlock Audio Lesson
A set of vectors is orthonormal if they are orthogonal and each vector has a unit length. That means their inner product is one when taken with themselves. Can someone give an example of what this means?
If we have vectors like { (1, 0), (0, 1) }, they are both orthogonal and have a length of 1.
Great example! This property makes computation very efficient. Can anyone think of applications for orthonormal sets in engineering?
In structural analysis, maybe we could use orthonormal sets for calculating forces easily?
Exactly! Orthonormal sets play a crucial role in simplifying calculations in various engineering contexts. Now, let’s discuss the Gram-Schmidt process.
Exploring the Gram-Schmidt Process
Unlock Audio Lesson
The Gram-Schmidt process allows us to take any linearly independent set of vectors and produce an orthonormal set. Who can summarize how it works?
We start with a set of vectors and then adjust them step by step, projecting onto each subsequent vector to eliminate components and create orthonormal ones.
Precisely! It’s a systematic way of ensuring orthogonality while maintaining span. How does this relate back to our engineering applications?
It can help ensure that analyses are accurate and prevent numerical errors in simulations.
Absolutely! Understanding this process is crucial for working in finite element analysis and more. Let's summarize what we’ve learned.
Summary of Key Concepts
Unlock Audio Lesson
As we wrap up, can anyone summarize the key points we covered today about orthogonality and orthonormal sets?
We learned that orthogonal vectors have an inner product of zero, and orthonormal vectors are both orthogonal and unit vectors.
And we discussed the Gram-Schmidt process to create orthonormal sets from any independent vector set!
Great summaries! Always remember these concepts are not just theoretical; they have practical applications in various engineering fields.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains that two vectors are orthogonal if their inner product is zero, while a set of vectors is orthonormal if they are both orthogonal and each vector is a unit vector. Additionally, it covers the Gram-Schmidt orthonormalization process and its applications.
Detailed
Orthogonality and Orthonormal Sets
In vector spaces, two vectors u and v are said to be orthogonal if their inner product ⟨u, v⟩ equals zero:
Definition of Orthogonality
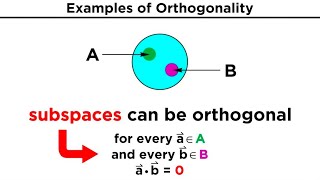
- Orthogonality implies that the vectors are at right angles (90 degrees) to each other, which has important implications in geometry and algebra.
Orthonormal Sets
- A set of vectors {v₁, v₂, ..., vₖ} is considered orthonormal if:
- Orthogonal: The inner product between any two different vectors in the set is zero, ⟨vᵢ, vⱼ⟩ = 0 for i ≠ j.
- Unit vectors: The inner product of each vector with itself is one, ⟨vᵢ, vᵢ⟩ = 1 for all i.
Gram-Schmidt Orthonormalization Process
- The Gram-Schmidt process is a method for converting a linearly independent set of vectors into an orthonormal set that spans the same subspace. This is vital in numerical methods, finite element modeling, and solving least squares problems, making computations efficient and ensuring stability in mathematical models.
Significance
Understanding orthogonality and orthonormality is crucial for Civil Engineering applications, as these concepts simplify calculations in various engineering problems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Orthogonality of Vectors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Two vectors u and v are said to be orthogonal if ⟨u, v⟩ = 0.
Detailed Explanation
Orthogonality is a fundamental concept in vector spaces. When two vectors u and v are orthogonal, it means they are at right angles to each other in a geometric sense. This relationship can be mathematically described using an inner product (or dot product), denoted as ⟨u, v⟩. If this inner product equals zero, then the vectors u and v are orthogonal. This concept is crucial in fields like graphics, engineering, and physics, where perpendicular vectors simplify calculations and interpretations.
Examples & Analogies
Imagine standing at the corner of a room where two walls meet. Each wall represents a vector, and together they form an L-shape. Since the walls are at a right angle to each other, we can say these two walls (or vectors) are orthogonal. Just as you can visualize how one wall is perpendicular to the other, in mathematics, orthogonality indicates that the interaction between these vectors (the area of influence) does not overlap when using the inner product.
Orthonormal Sets
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A set of vectors {v₁, v₂, ..., vₙ} is orthonormal if:
- ⟨vᵢ, vⱼ⟩ = 0 for i ≠ j (orthogonal)
- ⟨vᵢ, vᵢ⟩ = 1 for all i (unit vectors)
Detailed Explanation
An orthonormal set of vectors is a collection of vectors that not only are orthogonal (perpendicular to each other) but also each have a unit length, meaning the inner product of any vector with itself equals one. In a mathematical sense, this means that all vectors in the set are both orthogonal to each other and normalized to a length of one. Orthonormal sets are particularly useful because they simplify many operations in vector spaces, including projections and transformations.
Examples & Analogies
Think of a basketball court where each player stands at a specific position on the court. If one player stands directly at the three-point line (unit position), and the others are evenly spaced around the court and not overlapping, these players represent an orthonormal set. Just as each player’s position can be described perfectly without confusion (no overlap and all equal distances), an orthonormal set allows mathematical analysis to remain clean and straightforward when applying transformations or calculations.
Gram-Schmidt Orthonormalization Process
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Gram-Schmidt Orthonormalization Process is a method for converting a linearly independent set of vectors into an orthonormal set while spanning the same subspace.
Detailed Explanation
The Gram-Schmidt process takes a set of linearly independent vectors and transforms them into an orthonormal set. This is done through a step-by-step approach where each vector is adjusted to be orthogonal to those previously processed, then normalized to ensure each has a unit length. The significance of this process lies in its application in numerical methods, finite element modeling, and solving least-squares problems, as it allows for simplified calculations and clearer geometric interpretations.
Examples & Analogies
Consider a team of dancers learning a new choreography. Initially, they might be dancing in various formations without any specific order. The director observes their moves and gradually corrects their positions to ensure each dancer is correctly aligned (orthogonal) and maintaining their own space (normalization). By the end of the practice, the dancers form a neat, synchronized formation, similar to how the Gram-Schmidt process organizes vectors into an orthonormal set.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Orthogonality: When two vectors are perpendicular with an inner product of zero.
-
Orthonormal Set: A collection of vectors that are both orthogonal and have unit length.
-
Inner Product: A calculation that provides insight into the angle and magnitude relationship between vectors.
-
Gram-Schmidt Process: A technique to convert a linearly independent set of vectors into an orthogonal set.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If vectors u = (1, 0) and v = (0, 1), they are orthogonal since ⟨u, v⟩ = 0.
-
The vectors (1/sqrt(2), 1/sqrt(2)) and (-1/sqrt(2), 1/sqrt(2)) form an orthonormal set.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Vectors meet at right angles true, orthogonality helps us pursue.
📖 Fascinating Stories
-
Imagine two friends standing at the corner of a street, one facing north and the other facing east. Their directions are orthogonal, just like orthogonal vectors in mathematics!
🧠 Other Memory Gems
-
O for Orthogonal, O for zero. Remember, orthogonality means no overlap in terms!
🎯 Super Acronyms
O.U.R. - Orthonormal = Unit length + Right angles.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Orthogonality
Definition:
A property of vectors indicating they are perpendicular, characterized by an inner product of zero.
-
Term: Orthonormal Set
Definition:
A set of vectors that are orthogonal to each other and each has a norm of one.
-
Term: Inner Product
Definition:
A mathematical operation that takes two vectors and returns a scalar, reflecting both the length and angle between them.
-
Term: GramSchmidt Process
Definition:
A method for converting a set of linearly independent vectors into an orthonormal set.