Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Infinite-Dimensional Spaces
Unlock Audio Lesson
Today, we'll start discussing infinite-dimensional vector spaces. Can anyone tell me what makes a vector space infinite-dimensional?
Is it that you can't describe it with a finite set of vectors?
Exactly! Infinite-dimensional spaces cannot be spanned by a finite collection of vectors. For example, the space of all polynomials is infinite-dimensional.
What about functions? Are they also infinite-dimensional?
Great question! Yes, the space of all real-valued continuous functions defined over an interval is another example of an infinite-dimensional vector space. Remember, it's crucial for applications in various fields!
So, is every infinite-dimensional space somehow related to an infinite number of dimensions?
That's right! Infinite dimensions often imply an infinite basis, which relates to the idea of span and linear independence in these spaces.
Applications of Infinite-Dimensional Spaces
Unlock Audio Lesson
Let’s discuss the applications of infinite-dimensional vector spaces. Can anyone name one application, especially in engineering or applied mathematics?
I think Fourier transforms are one of them!
That's correct! Fourier transforms decompose functions into frequencies, which allows us to analyze vibrational behavior in engineering systems.
Are there any other applications?
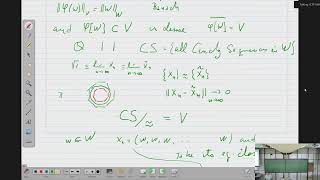
Yes! Infinite-dimensional spaces are also prominent in functional analysis, where we study spaces of functions and their transformations, aiding in solving differential equations.
How does this relate to civil engineering?
In civil engineering, understanding these concepts helps analyze complex structures and systems. For example, in continuum mechanics, function spaces model materials under stress.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses infinite-dimensional vector spaces, highlighting their characteristics and significance in various applications such as Fourier series and functional analysis. These spaces are essential in the study of mathematics and its applications in fields like engineering.
Detailed
Infinite-Dimensional Vector Spaces
Infinite-dimensional vector spaces are defined as vector spaces that cannot be spanned by a finite set of vectors. These spaces encompass sets such as the collection of all polynomials or all continuously defined functions over a given interval. They are fundamental in various areas of mathematics and engineering, particularly within functional analysis and differential equations.
Key Applications:
- Fourier Series and Transforms: Essential for analyzing vibrations and wave propagation, these tools leverage infinite-dimensional spaces to decompose functions into their constituent frequencies.
- Functional Analysis: This branch of mathematical analysis deals with spaces of functions and their properties, extending the concept of vector spaces to infinite dimensions. It facilitates the study of linear operators and their applications in differential equations, making it highly relevant in civil engineering and other fields.
As such, understanding infinite-dimensional vector spaces is critical for students of mathematics and various applied disciplines, including civil engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Infinite-Dimensional Vector Spaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Spaces like the set of all polynomials, functions, or sequences are infinite-dimensional.
Detailed Explanation
Infinite-dimensional vector spaces are structures where the set of elements (vectors) cannot be fully captured by a finite number of basis vectors. This means that no matter how many vectors you use to describe the space, there will always be more vectors that can be included. For example, consider the vector space of all polynomials—no single polynomial can represent all possible polynomials, and as you increase the degree of the polynomial, the vector space continues to grow infinitely.
Examples & Analogies
Think of an infinite-dimensional vector space like a library of books. If the library only had a finite number of books, you could describe all the knowledge contained in it with a limited number of subjects or titles. However, as new books are continuously written, the knowledge base grows indefinitely. Similarly, in infinite-dimensional spaces, the number of ways to combine elements grows endlessly, reflecting an ever-expanding set of possibilities.
Applications of Infinite-Dimensional Spaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Applications include:
- Fourier Series and Transforms in analyzing vibrations and wave propagation
- Functional Analysis in continuum mechanics and differential equations
Detailed Explanation
Infinite-dimensional vector spaces have significant applications in various fields of science and engineering. For example, Fourier Series and Transforms use these spaces to decompose functions into simpler sine and cosine components, which is especially useful in analyzing periodic signals, vibrations, and wave propagation. Functional Analysis, another branch that utilizes infinite-dimensional spaces, deals with understanding functions as vectors themselves, allowing us to solve complex problems in mechanics and differential equations by treating functions as elements in a vector space.
Examples & Analogies
Imagine you are trying to analyze music. Each musical note can be viewed as a wave that can be broken down into simpler waves with sine and cosine functions, much like how we break down complex functions in mathematics using Fourier series. This decomposition helps sound engineers understand and manipulate sound waves in recording and production—the concept mirrors how infinite-dimensional spaces allow mathematicians and engineers to understand and solve complex equations by treating a function as a vector.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Infinite-dimensional vector spaces: Cannot be described by a finite set of vectors.
-
Application in Fourier transforms: Key tool in analyzing frequencies in functions.
-
Functional analysis importance: Critical in understanding operator theory in engineering.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
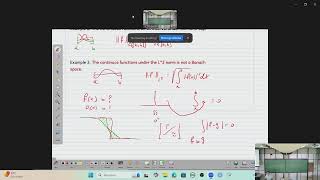
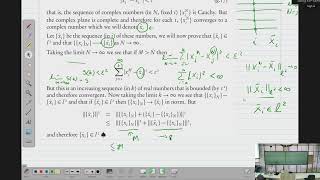
The set of all functions defined on an interval [a, b] over the reals is an infinite-dimensional vector space.
-
The space of polynomials of arbitrary degree cannot be spanned by a finite number of polynomial basis functions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In dimensions that stretch far and wide, vectors are all at their side. Infinite spaces can’t be contained, in functions and sequences they’re aptly trained.
📖 Fascinating Stories
-
Imagine a music factory where notes blend to create songs. Each song is like a function, layered with rhythms and tones, showing how infinite-dimensional spaces go beyond finite frameworks.
🧠 Other Memory Gems
-
F-Fan: Fourier, Functional - Remember these in infinite-dimensional fathoms.
🎯 Super Acronyms
IVS - Infinite Vector Spaces.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: InfiniteDimensional Vector Space
Definition:
A vector space that cannot be spanned by a finite set of vectors, often including functions or sequences.
-
Term: Fourier Series
Definition:
A way to represent a function as a sum of simple sine waves, crucial in signal processing.
-
Term: Functional Analysis
Definition:
A branch of mathematical analysis dealing with spaces of functions and linear operators.
-
Term: Span
Definition:
The set of all possible linear combinations of a given set of vectors.
-
Term: Linear Operator
Definition:
A mapping between two vector spaces that preserves the operations of vector addition and scalar multiplication.