Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Quotient Spaces
Unlock Audio Lesson
Today, we'll explore quotient spaces. A quotient space is formed when we start with a vector space V and a subspace W. Can anyone tell me what a subspace is?
Isn't a subspace a smaller vector space within a bigger one?
Exactly! Now, when we create cosets like v + W, what do you think that means?
It means we are taking a vector v and adding all the vectors in W to it.
Correct! This forms a set of vectors, and that's what we call a coset. So the quotient space V/W is the collection of all these cosets.
Why are we studying this?
Great question! Quotient spaces help simplify complex vector spaces, which is crucial in fields like theoretical mechanics and optimization.
In summary, a quotient space allows us to take a vector and consider all the vectors that differ from it by any vector in W. Understanding this concept is vital for progressing into more complex applications.
Applications of Quotient Spaces
Unlock Audio Lesson
Next, let’s talk about how quotient spaces are applied in engineering. Can anyone think of a scenario where this concept might be useful?
Maybe in structural analysis where we simplify forces?
Yes! By 'modding out' a subspace, you can simplify the analysis of forces acting on a structure. This allows engineers to focus on the essential behaviors without being overwhelmed by extraneous details.
So, it's like only measuring the relevant forces affecting a beam without considering redundant constraints?
Exactly! You are catching on quickly. And to reinforce, quotient spaces can also help in areas like optimization by reducing problem dimensions.
For instance, in optimization problems, using quotient spaces can lead to simplified constraints, making it easier to find optimal solutions.
To summarize, quotient spaces are a powerful tool that help us simplify and manage complexity, which is indispensable in many engineering disciplines.
Understanding Cosets
Unlock Audio Lesson
Let’s take closer look at cosets. Does anyone remember the definition of a coset?
It's the set of all vectors you can form by adding W to a vector v, right?
Exactly right! Each coset is like a 'shift' of the subspace W. Can you visualize this?
Kind of like translating a shape in geometry? Each coset is a different copy of the subspace moved to different locations.
Precisely! This geometric interpretation helps us understand how these structures fit together in V.
So we're making different versions of the same subspace across V?
That's right! Each coset captures a unique aspect of the vector space by showing how different vectors relate to the subspace. Remember, understanding cosets gives you insight into the broader structure of V.
In summary, viewing cosets as copies of a subspace aids in comprehending their roles within the entire vector space.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses quotient spaces created by partitioning a vector space V into cosets formed by a subspace W. This concept is significant in theoretical mechanics and optimization, facilitating the study of vector spaces by reducing complexity.
Detailed
Quotient Spaces
In linear algebra, a quotient space, denoted as V/W, is the set of all cosets formed by pairing elements of a vector space V with a subspace W. The coset of an element v in V, represented by v + W, consists of all vectors that can be expressed in the form of v plus an element from the subspace W. This method of partitioning helps in understanding the structure of vector spaces more deeply by creating equivalence classes of vectors. Quotient spaces are particularly useful in applications such as theoretical mechanics and optimization because they simplify problems by reducing dimensionality, allowing engineers and mathematicians to focus on essential properties without excessive complexity. Understanding quotient spaces is crucial as it expands the toolkit available for analyzing vector spaces in various contexts, especially in advanced engineering applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Quotient Spaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
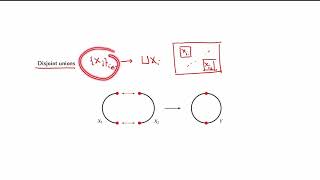
Let W be a subspace of V. The quotient space V/W is the set of all cosets: v + W = {v + w | w ∈ W}
Detailed Explanation
A quotient space is created by taking a vector space V and a subspace W and forming a new space that consists of cosets. A coset of W is a set of vectors formed by adding a specific vector v to every vector in W. This means that for each vector v in the vector space V, you can generate a set of new vectors by adding v to each of the vectors in the subspace W. The result is a collection of vectors that are treated as a single entity within the context of the quotient space V/W.
Examples & Analogies
Consider a group of people in a room representing the vector space V. If we think of a particular subgroup (like a family) as the subspace W, the quotient space V/W represents distinct groups of people who are not part of that family. Each group (coset) consists of all individuals who can be reached by adding themselves to each family member. Each group is like a set of coordinates drawn from the same starting point, creating a new perspective based on that family dynamic.
Simplification through Quotient Spaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This concept helps simplify complex vector spaces by 'modding out' a subspace, making it useful in theoretical mechanics and optimization.
Detailed Explanation
In mathematics and engineering, quotient spaces can be powerful tools for simplifying complex problems. By 'modding out' (or factoring out) a subspace, you reduce the overall complexity of the vector space V, focusing only on the structures that are not influenced by the elements of W. This simplification can reveal insights into the geometry of the situation, provide clarity in analysis, and make computations significantly easier, especially in fields like theoretical mechanics and optimization where understanding the core vector relationships is crucial.
Examples & Analogies
Imagine you are analyzing a complex traffic system where the paths of several routes are similar due to road closures (the subspace W). Instead of assessing all routes in their entirety, you could focus on the essential stretches of the road that are unaffected by the closures, creating a new map that simplifies the navigation process. This new map, or quotient space, allows you to observe the necessary alternatives without duplicating considerations of blocked routes, making your traffic analysis more efficient.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Quotient Space: The set of cosets formed by a vector space V over a subspace W.
-
Coset: The collection of a vector combined with every vector in a subspace.
-
Subspace: A smaller vector space within a larger vector space that adheres to vector space properties.
-
Dimensionality Reduction: The process facilitated by quotient spaces to simplify complex spaces.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
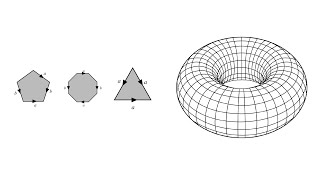
If V is R² and W is the x-axis, each coset in V/W represents a line parallel to the x-axis. V/W captures the vertical dimensions of the space.
-
In control theory, if a system's state can be partitioned into states differing by a constant offset, then each offset is represented as a coset in a quotient space derived from the original state space.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In spaces we partition, with a plan, / Cosets are formed, that's our span!
📖 Fascinating Stories
-
Imagine a workshop where each worker represents a vector, and their tools represent elements in W. As they gather their tools, they can form different 'groups' or cosets, allowing us to visualize their collective capabilities.
🧠 Other Memory Gems
-
Think COSS (Cosets = Original + Subspace Shift) to remember how cosets are formed.
🎯 Super Acronyms
QUOT (Quotient = Unique group of ordered tools) helps recall that the quotient space is grouping vectors based on a subspace.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Quotient Space
Definition:
A vector space V divided by a subspace W, represented as V/W, consisting of cosets formed by adding elements from W to vectors from V.
-
Term: Coset
Definition:
A set that includes a vector v along with all vectors from a subspace W, expressed as v + W.
-
Term: Subspace
Definition:
A subset of a vector space that is also a vector space under the same operations.
-
Term: Vector Space
Definition:
A mathematical structure consisting of vectors, where vector addition and scalar multiplication are defined.