Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Definition of Dual Spaces
Unlock Audio Lesson
Today, we're talking about dual spaces. The dual space V* of a vector space V consists of all linear functionals from V to the field 𝔽. Can someone tell me what a linear functional does?
Isn't it a map that takes vectors and gives us back a number in the field?
Exactly! A linear functional f has this property: for any vectors u and v in V, and scalars a and b in 𝔽, if we scale and add, we can distribute the functional: f(a·u + b·v) = a·f(u) + b·f(v). This shows how linear it is.
So every linear functional preserves the operations of addition and scalar multiplication?
That's right! This linearity is key. Let's remember this property with the acronym P.O.A. — Preserves Operations in Addition!
Applications of Dual Spaces
Unlock Audio Lesson
Now that we understand dual spaces, let's discuss their significance in engineering. Who can think of an application where dual spaces are relevant?
What about in variational principles like virtual work in mechanics?
Great example! In virtual work principles, we use dual spaces to represent energy states. Also, do you remember how we talked about stress and strain?
Yes, they are represented through energies, right?
Correct! Stress-strain energy considerations often invoke dual spaces to relate vectors with energies. It's fascinating how these abstract concepts have very concrete uses!
Properties and Structures of Dual Spaces
Unlock Audio Lesson
Let's dive deeper into the structures of dual spaces. Can anyone summarize why dual spaces are considered significant?
They help connect linear functionals with the vector space and have practical uses.
Exactly! Furthermore, studying the relationship between a vector space and its dual space enhances our understanding of the dimensions involved. Do you recall how many dimensions a dual space has?
Isn't it the same as the original vector space?
Absolutely! The dimension of V* is equal to the dimension of V. To remember this, think of it as D for Dual, and also D for Dimension being equal!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explores the concept of dual spaces, defining what a dual space is and its relevance, particularly in engineering applications, where linear functionals are essential in variational principles and energy representations.
Detailed
Dual Spaces
The dual space, denoted as V, of a vector space V is the set of all linear functionals that can be defined from V to the field 𝔽. A linear functional is a function f: V → 𝔽, which satisfies the following property: for all vectors u, v in V and all scalars a, b in 𝔽, it holds that f(a·u + b·v) = a·f(u) + b·f(v)*. This linearity is crucial as it maintains the structure of vector spaces in functional form.
Dual spaces are significant in various fields, particularly in engineering applications where variational principles are applicable, such as the concept of virtual work in mechanics. They also play a role in stress-strain energy representations, highlighting their importance in both the theoretical and practical aspects of civil engineering. Through understanding dual spaces, students can appreciate how linear mappings interact and represent changes in engineering contexts.
Youtube Videos
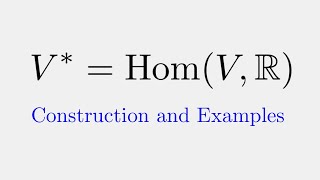
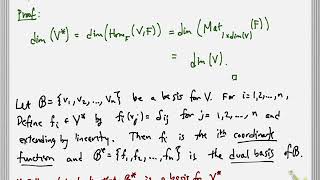
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Dual Spaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The dual space V* of a vector space V is the set of all linear functionals from V to 𝔽.
Detailed Explanation
A dual space is constructed from a given vector space, V. The dual space, denoted as V*, consists of all linear functionals, which are special types of functions that take a vector from V and return a scalar from the field 𝔽. Linear functionals are linear mappings, meaning they adhere to the properties of superposition: they preserve addition and scalar multiplication. Specifically, if 'f' is a linear functional, it satisfies the property that f(a·u + b·v) = a·f(u) + b·f(v) for any vectors u, v in V and scalars a, b in 𝔽.
Examples & Analogies
Think of the dual space like a translator who converts vectors into understandable values (scalars). Just like a translator takes sentences (the vectors) and interprets them into meaningful information (the scalars), linear functionals interpret vectors from the vector space into real numbers.
Properties of Linear Functionals
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A linear functional is a map f: V → 𝔽 such that: f(a·u + b·v) = a·f(u) + b·f(v)
Detailed Explanation
The defining property of linear functionals indicates that they respect the addition and scalar multiplication of vectors. This means that if you scale a vector or add two vectors, the functional will react in a predictable way according to these operations. The efficiency of linear functionals is significant in various applications, as they allow for simplifications and computations in fields like mechanics and engineering.
Examples & Analogies
Imagine you have a machine that measures weights (the linear functional), and you are placing different weights (the vectors) on the scale. If you add two weights together, the machine will give you the combined weight – this mimics how a linear functional processes vectors through addition and scalar multiplication.
Importance of Dual Spaces in Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Significance in Engineering: • Appears in variational principles, e.g., virtual work in mechanics • Used in stress-strain energy representation
Detailed Explanation
Dual spaces play a critical role in engineering, particularly in mechanics and materials science. Variational principles, which are foundational to deriving equations governing physical systems, often utilize concepts from dual spaces. For instance, in the context of virtual work, dual spaces allow engineers to relate the work done by forces to displacements in a systematic way, facilitating problem-solving in structures and materials under various loads.
Examples & Analogies
Consider a situation where an engineer is designing a bridge. They use virtual work principles to calculate how forces affect the bridge's structure as it bends under load. By utilizing dual spaces, they can predict how much energy is absorbed by the materials during this bending, ensuring safety and reliability.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Dual Space: The space of all linear functionals from V to 𝔽.
-
Linear Functional: A mapping that preserves vector addition and scalar multiplication.
-
Variational Principles: Principles that utilize dual spaces in engineering applications.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In structural engineering, dual spaces are used in the analysis of energy states through linear functionals representing stresses.
-
Mathematical optimization problems often employ dual spaces to derive conditions for minima or maxima based on linear functionals.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
A dual space is quite the ace, where functionals meet their place.
📖 Fascinating Stories
-
Imagine a magician who can turn every vector into a number, summoning the magic of linear functionals.
🧠 Other Memory Gems
-
D.F.L. - Dual Spaces Foster Linearity.
🎯 Super Acronyms
D = Dimension of the dual space is equal to the dimension of the vector space.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Dual Space
Definition:
The dual space V* consists of all linear functionals from a vector space V to the field 𝔽.
-
Term: Linear Functional
Definition:
A map f: V → 𝔽 that satisfies the property f(a·u + b·v) = a·f(u) + b·f(v).
-
Term: Variational Principles
Definition:
A principle in mechanics that states that the actual path or configuration of a system is such that it minimizes or extremizes some quantity.
-
Term: Field
Definition:
A set equipped with two operations (addition and multiplication) that satisfy the properties of commutativity, associativity, distributivity, and have identity elements.