Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Definition of Inner Product Spaces
Unlock Audio Lesson
Today, we'll dive into inner product spaces. An inner product space is essentially a vector space that comes with an inner product. This inner product allows us to measure angles and lengths within the space, which is quite useful. Can anyone tell me why we might want to measure angles or lengths in a vector space?
To understand how vectors interact with each other, maybe?
Exactly! For instance, we can define when two vectors are orthogonal. But what does orthogonality mean in this context?
It means they are at right angles to each other, right?
Correct! In inner product spaces, two vectors are considered orthogonal if their inner product is zero. Remember this: O for Orthogonal, O for 'Output = Zero' in the inner product. Now, who can summarize the three properties that an inner product must satisfy?
Uh, there's conjugate symmetry, linearity, and positive-definiteness, right?
Great job! Let's keep these in mind as we discuss how they work practically.
Properties of Inner Products
Unlock Audio Lesson
Let's break down the properties more closely. First up, conjugate symmetry. Can someone explain how this property works?
It means that ⟨u, v⟩ is the same as ⟨v, u⟩?
Exactly! And how about linearity in the first argument?
That means we can factor out scalars and combine vectors inside the inner product.
Yes! This property is fundamental in ensuring that our inner product behaves nicely with vector addition and scalar multiplication. Now, the last one: positive-definiteness?
It ensures that the product of a vector with itself is always non-negative and is zero only if the vector is the zero vector.
Perfect! Remember this sequence: C for Conjugate, L for Linearity, and P for Positive-definiteness, or CLP. Let's put the pieces together with an example.
Applications of Inner Product Spaces
Unlock Audio Lesson
We’ve covered the theory; now let’s look at applications. Inner products are crucial in calculating angles between vectors. Why would this matter in engineering?
It helps us determine if forces are acting in perpendicular directions, which is crucial for stability.
Exactly! In structural analysis, knowing if force systems are orthogonal can impact design decisions. Additionally, can anyone explain how the inner product is computed in ℝ² or ℝ³?
We just take the dot product of their coordinates, like multiplying corresponding components and summing up the results.
Yes! In this example, for vectors u = (1, 2) and v = (3, 4), it's ⟨u, v⟩ = 1*3 + 2*4 = 11. Keep this formula handy! Wrapping up, what are the key takeaways from today?
We learned what inner product spaces are, their properties, and their applications!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section covers the definition and properties of inner product spaces, including conjugate symmetry, linearity, and positive-definiteness. It highlights the significance of inner products in applications like measuring angles and defining orthogonality.
Detailed
Inner Product Spaces
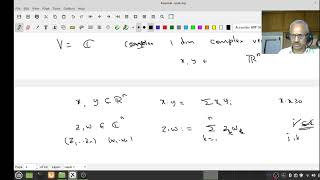
An inner product space is characterized as a vector space V along with a binary operation, termed the inner product, represented as ⟨·,·⟩: V × V → ℝ. This inner product must satisfy three key properties: conjugate symmetry, linearity in the first argument, and positive-definiteness. Conjugate symmetry implies that swapping the inputs produces the same output, while linearity signifies that the inner product is linear in its first argument. Positive-definiteness guarantees that the inner product of a vector with itself is non-negative, resulting in zero if and only if the vector is the zero vector itself.
Example: In the Euclidean space ℝⁿ, the inner product takes the form ⟨u, v⟩ = ∑ uᵢvᵢ, which calculates the sum of the products of the corresponding components of two vectors.
Applications: Inner products are pivotal in various fields, particularly in calculations involving angles and lengths in vector spaces. They help define concepts such as orthogonality and orthonormality. In civil engineering contexts, they are utilized to determine orthogonal force systems in structural analysis.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of an Inner Product Space
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
An inner product space is a vector space V along with an inner product ⟨·,·⟩: V × V → ℝ that satisfies:
1. Conjugate symmetry: ⟨u, v⟩ = ⟨v, u⟩
2. Linearity in the first argument: ⟨au + bv, w⟩ = a⟨u, w⟩ + b⟨v, w⟩
3. Positive-definiteness: ⟨v, v⟩ ≥ 0 with equality iff v = 0
Detailed Explanation
An inner product space combines both the features of a vector space and a specific kind of product, known as the inner product. The vector space V is where we can perform vector addition and scalar multiplication.
- Conjugate Symmetry states that the inner product of vector u with vector v is equal to the inner product of vector v with vector u. This property ensures that the measure of 'interaction' between two vectors remains the same regardless of the order of these vectors.
- Linearity in the First Argument implies that when you take a linear combination of vectors (the first argument) and compute the inner product with a third vector (the second argument), it can be distributed across the sum. This means you can separate the combinations and work with them individually.
- Positive-Definiteness ensures that the inner product of a vector with itself is always non-negative and is zero only if the vector itself is the zero vector. This condition confirms that the inner product behaves like a 'length' or 'magnitude'.
Examples & Analogies
Think of an inner product space like a classroom where different students (vectors) interact. The inner product reflects the conversation (the inner product operation) between two students. Just like how students can speak to each other in any order (conjugate symmetry), one student can also discuss different topics with another (linearity). However, if there’s no interaction, it’s like one student being absent (positive-definiteness), meaning no conversation can take place.
Example: Euclidean Inner Product
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For u = (u₁, u₂, ..., uₙ), v = (v₁, v₂, ..., vₙ), ⟨u, v⟩ = ∑ uᵢvᵢ
Detailed Explanation
In the context of Euclidean space, the inner product of two vectors can be computed using the dot product. If you have two vectors u and v each represented by their coordinates in n-dimensional space, you can find their inner product by multiplying corresponding components of the vectors together and then summing these products:
For example, if u = (2, 3) and v = (4, 5), the inner product ⟨u, v⟩ = (2 * 4) + (3 * 5) = 8 + 15 = 23. This result gives a measure of how much one vector extends in the direction of another, analogous to the angle between the two vectors. This is important for determining orthogonality and angles between vectors.
Examples & Analogies
Imagine you are taking a hike with a map that requires you to determine how directly you are moving towards your destination. Each step can be thought of as a vector, where the inner product tells you how well your movement aligns with the direction to your destination. A higher inner product means you are headed more directly towards your goal, just like your hike is getting shorter with each well-placed step.
Applications of Inner Product Spaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Applications:
- Used in measuring angles and lengths
- Critical in defining orthogonality and orthonormality
- In structural analysis, inner products can help determine orthogonal force systems.
Detailed Explanation
Inner product spaces are fundamental in various applications due to their geometric interpretations. Here are a few key applications:
- Measuring Angles and Lengths: The inner product helps calculate angles between vectors. If the inner product is zero, it indicates orthogonality, meaning the vectors are at a right angle. Similarly, the length of a vector can be derived from its inner product with itself, similar to finding the distance from a point to the origin.
- Defining Orthogonality and Orthonormality: Vectors are orthogonal if their inner product equals zero. If they are also of unit length, they are said to be orthonormal.
- Structural Analysis: In engineering, inner products help analyze force systems by determining if force vectors are acting perpendicular (orthogonal) to certain structures, which is essential for stability in design.
Examples & Analogies
Consider a construction project where engineers are determining the strength of a beam against various forces. Using inner products, they can calculate whether the forces applied to the beam act perpendicularly to its length, which would indicate stability. Just like ensuring that the beams in a house are held in place at right angles makes the structure stronger, understanding the relationships between force vectors through inner products ensures sound engineering practices.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Inner Product Space: A vector space equipped with an inner product that allows geometric interpretations.
-
Conjugate Symmetry: Property that defines the inner product's output as equal by swapping vectors.
-
Positive-Definiteness: Ensures a vector's inner product with itself is non-negative.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In ℝ², the inner product of vectors u = (3, 4) and v = (1, 2) is ⟨u, v⟩ = 31 + 42 = 11.
-
In structural analysis, the inner product helps determine if two forces acting at a point are orthogonal, ensuring balance.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Inner products, oh so fine, they measure angles every time!
📖 Fascinating Stories
-
Imagine a world where vectors dance; they twirl and intertwine, yet when two are orthogonal, they stand apart, each with a perfect angle at their start!
🧠 Other Memory Gems
-
C.L.P. for Conjugate, Linearity, Positive-Definiteness, the key in inner product space!
🎯 Super Acronyms
O.O for O for Orthogonal, O for Output = Zero when two vectors align!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Inner Product
Definition:
A binary operation on a vector space that returns a scalar, satisfying properties such as conjugate symmetry and positive definiteness.
-
Term: Orthogonality
Definition:
The condition where two vectors are perpendicular to each other, indicated by an inner product of zero.
-
Term: PositiveDefiniteness
Definition:
A property of an inner product ensuring that the inner product of a vector with itself is non-negative, being zero only for the zero vector.