Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Rank
Unlock Audio Lesson
Today, we're diving into the concepts of rank and nullity. Let's start with rank. Can anyone tell me what they think rank refers to in a matrix context?
Is it about how many rows the matrix has?
Close! Rank actually refers to the number of linearly independent columns in the matrix. It's a measure of how much information is captured by these columns.
What does it tell us about the matrix then?
Great question! Higher rank usually indicates a stronger ability to represent various data relationships. Remember: R for 'Representation' stands for Rank!
So, how do we actually compute the rank?
We can find the rank through row reduction to echelon form. By doing this, we can easily identify the pivot columns that contribute to the rank.
Can a matrix have a rank higher than the number of its rows?
No, it cannot! The rank cannot exceed either the number of rows or the number of columns. So, keep that in mind.
To summarize, the rank measures the linear independence of columns and indicates the capacity of the matrix to convey information.
Introduction to Nullity
Unlock Audio Lesson
Now let's shift gears and talk about nullity. Who can tell me what nullity might refer to?
Is it to do with the solutions of a matrix equation?
Exactly! Nullity is the dimension of the null space, which consists of all solutions to the equation Ax = 0. A high nullity indicates many solutions exist!
How do we find the nullity, though?
To find nullity, we can use the relationship: nullity(A) = n - rank(A), where n is the number of columns. This helps us link nullity with the rank.
That means if a matrix has full rank, its nullity is zero!
Exactly right! If the rank equals the number of columns, the null space contains only the zero vector.
To recap, nullity shows how many 'free' variables we have in our system, and it's tightly connected to rank.
Rank-Nullity Theorem
Unlock Audio Lesson
Now that we've tackled rank and nullity, let's discuss the Rank-Nullity Theorem. Who can summarize what that states?
Does it say that rank plus nullity equals the number of columns in a matrix?
Spot on! This theorem gives us a powerful relationship between the dimensions of the column space and null space of matrix A.
How would this be useful in practical scenarios?
Understanding this theorem helps when solving systems of equations. If you know the rank, you can determine the number of solutions right away.
So if we have a matrix where rank is 2 and it has 5 columns, we could expect 3 free variables?
Correct! And that's crucial for predicting the nature of solutions in linear systems.
In summary, the Rank-Nullity Theorem is key for linking the number of solutions to system constraints, aiding effective problem-solving.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Rank and nullity are essential concepts in linear algebra related to matrices. The rank of a matrix represents the dimension of its column space, while the nullity determines the dimension of its null space. Together, they adhere to the Rank-Nullity Theorem, which states that the sum of rank and nullity equals the number of columns in the matrix.
Detailed
Rank and Nullity
In linear algebra, the concepts of rank and nullity provide a deeper understanding of the characteristics of matrices.
- Rank (rank(A)): It refers to the dimension of the column space (or row space) of a matrix A, indicating how many linearly independent column vectors there are in A. The higher the rank, the more information the matrix can convey in terms of solutions to linear equations.
- Nullity (nullity(A)): It denotes the dimension of the null space of the matrix A, which consists of all solutions to the equation Ax = 0. Essentially, nullity gives insights into the number of free variables in a linear system defined by the matrix A.
The relationship between these two dimensions is articulated in the Rank-Nullity Theorem, which asserts that for any matrix A of size m x n, the sum of the rank and nullity equals n (the number of columns in A). This theorem is pivotal in understanding the solutions to systems of linear equations, as it unequivocally relates the constraints imposed by the matrix to its degrees of freedom.
Youtube Videos
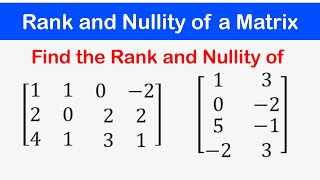
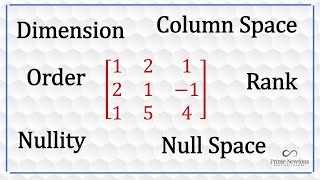
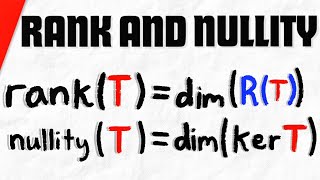
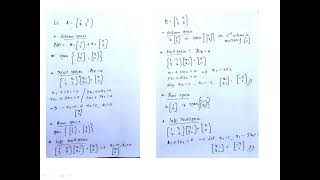
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Rank
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Rank of A = dimension of column space (or row space)
Detailed Explanation
The rank of a matrix A is defined as the dimension of its column space, which is the number of linearly independent columns in the matrix. This essentially tells us how many vectors in the matrix can provide unique directions in the vector space. Similarly, it can also be seen as the dimension of the row space. Understanding rank is crucial as it reflects the amount of information the matrix holds and is key to solving systems of linear equations.
Examples & Analogies
Consider a company that runs a survey to understand employee satisfaction across different departments. Each department's responses represent a column in a matrix. If two departments have very similar views, they 'add nothing new' to the overall understanding, hence decrease 'rank'. The higher the rank, the more unique insights are gained from diverse departments.
Definition of Nullity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Nullity of A = dimension of null space
Detailed Explanation
Nullity refers to the dimension of the null space of the matrix A. The null space is the set of all solutions to the homogeneous equation Ax = 0. It indicates how many vectors can be transformed into the zero vector, showing us the 'deficiency' in the information that A provides. Essentially, if nullity is high, it suggests that there are many solutions to the system of equations defined by A, making it less constrained.
Examples & Analogies
Imagine a factory that produces widgets. If there are multiple ways to rearrange the machinery (or processes) that result in no widgets being produced, each arrangement corresponds to a vector in the null space. Thus, the nullity represents the 'freedom' or flexibility in how operations can be configured without leading to production.
Rank-Nullity Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
By the Rank–Nullity Theorem: If A is an m×n matrix, then rank(A) + nullity(A) = n.
Detailed Explanation
The Rank-Nullity Theorem is a fundamental result in linear algebra that shows a relationship between the rank and nullity of a matrix. Here, n refers to the number of columns in the matrix A. This theorem implies that the total number of columns can be divided into the number of columns that contribute to the rank (dimension of the column space) and those that contribute to the nullity (dimension of the null space). Therefore, if you know the rank of a matrix, you can easily find its nullity and vice versa.
Examples & Analogies
Think of a library (the matrix A) where each book (column) represents a unique piece of information. The rank indicates how many unique books are present, while the nullity represents the books that are duplicates or do not contribute new information. The total must add up to the number of shelves (n) the library uses for storage, as both unique and duplicate books fit within this total.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Rank: Indicates the dimension of the column space or row space, representing linear independence.
-
Nullity: Refers to the dimension of the null space, showing the number of free variables in the solution.
-
Rank-Nullity Theorem: The fundamental relationship that connects the rank and nullity to the total number of columns.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: For a matrix A with 3 columns where two columns are linearly independent, the rank is 2 and therefore the nullity is 1.
-
Example 2: Given a 4x3 matrix with full rank (3), the nullity would be 0, indicating no free variables.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Rank and nullity, side by side, help us know how solutions coincide.
📖 Fascinating Stories
-
Imagine a classroom where students are either asking questions (nullity) or presenting answers (rank). The balance helps everyone learn better!
🧠 Other Memory Gems
-
RANK - Remember: A Number of Knowledge (rank) gives insights, while Nullity Leads to Yes's in a system.
🎯 Super Acronyms
RANK
- 'Representing A New Knowledge' helps recall that rank represents information learned through the columns.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Rank
Definition:
The dimension of the column space or row space of a matrix, indicating the number of linearly independent columns.
-
Term: Nullity
Definition:
The dimension of the null space of a matrix, indicating the number of free variables in the equation Ax = 0.
-
Term: Column Space
Definition:
The span of the column vectors of a matrix, representing all possible linear combinations of its columns.
-
Term: Null Space
Definition:
The set of all vectors x that satisfy the equation Ax = 0, forming a subspace.
-
Term: RankNullity Theorem
Definition:
A theorem stating that for any m x n matrix, rank(A) + nullity(A) = n.