Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Direct Sums
Unlock Audio Lesson
Today, we'll start with the direct sum of vector spaces. Who can tell me what it means for a vector space to be expressed as a direct sum?
Does it mean we can combine two subspaces into one?
Good attempt! When we say V = U ⊕ W, it means every vector v in V can be uniquely expressed as v = u + w, where u is from U and w is from W. Can anyone tell me why it's important that U and W only intersect at the zero vector?
If they shared more than just the zero vector, then the representation wouldn't be unique!
Exactly! This uniqueness helps simplify complex problems. It's like separating several ingredients in a recipe for clarity. Remember, 'Unique Under Null' helps us recall the intersection point.
Real-world Applications of Direct Sums
Unlock Audio Lesson
Now, let's talk about where we can actually use this concept in engineering. Can anyone give me an example?
Could we use it in structural analysis?
Yes! In structural analysis, we break down complex structures into simpler parts that are independent of each other. This direct sum approach allows us to solve systems of equations more effectively. Think of it as splitting a large problem into tiny, manageable pieces.
I see! It's like using blocks to build a tall structure.
Precisely! Just like each block has its position and role. Let's remember the phrase 'Separate to Solve'.
Key Properties of Direct Sums
Unlock Audio Lesson
Let’s dive into the properties of direct sums. What do you think are the key criteria for a vector space to be classified as a direct sum?
There must be unique representations and no overlap except for the zero vector!
Great! That's a crucial aspect. Can someone summarize what U ⊕ W means in simpler terms?
It means you can form any vector in V using only parts from U and W without getting confused!
Correct! Remember the acronym 'UNIQUE' to keep these properties in mind: Unique representation, No overlap, Intersect only at zero. Let's keep practicing this!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
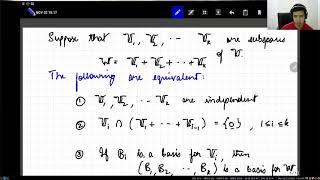
This section elaborates on the decomposition of a vector space into the direct sum of two subspaces. It defines the properties that must hold for such a decomposition, including uniqueness in representation and independence of subspaces, and highlights the significance of this concept in simplifying complex problems in engineering applications.
Detailed
In this section, we explore the concept of direct sums and decomposition within vector spaces. A vector space V can be expressed as the direct sum of two subspaces U and W, denoted as V = U ⊕ W, if each vector v in V can be uniquely represented as the sum of vectors from U and W, and if the intersection of U and W contains only the zero vector (i.e., U ∩ W = {0}). This decomposition is essential in various applications, allowing engineers and mathematicians to break down complex problems into simpler, independent components, which is particularly useful in fields like finite element analysis and dynamic systems. By understanding this concept, one gains insights into the structure and relationships within vector spaces, enhancing problem-solving capabilities.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Direct Sums
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A vector space V can be expressed as the direct sum of two subspaces U and W if:
- V = U ⊕ W
- Every v ∈ V can be uniquely written as v = u + w, where u ∈ U, w ∈ W
- U ∩ W = {0}
Detailed Explanation
The concept of a direct sum involves breaking a vector space into two distinct parts, U and W, that combine to reform the entire space V. To say that V = U ⊕ W means that every vector in V can be represented as the sum of a vector from U and a vector from W. Furthermore, each vector should be uniquely represented as such a sum. The condition U ∩ W = {0} indicates that U and W share only the zero vector, meaning they don't overlap in any other way. This ensures that the components are independent of each other.
Examples & Analogies
Imagine you have a room filled with two types of furniture: chairs and tables. The room represents the vector space V, chairs represent subspace U, and tables represent subspace W. Each piece of furniture can be clearly identified as either a chair or a table (no overlapping pieces), and every piece of furniture in the room can be described simply as either a chair or a table. In this analogy, the arrangement allows you to understand the function of each subspace while maintaining an organized overall structure.
Importance of Decomposition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This decomposition is useful in splitting problems into smaller, manageable independent components—important in solving systems of equations in FEM or dynamics.
Detailed Explanation
Decomposing a vector space into direct sums allows us to simplify complex problems by breaking them down into smaller, manageable components. In practical applications such as the Finite Element Method (FEM) used in engineering, this decomposition helps in analyzing structures by treating components independently. It lets us apply different methods to different parts of the problem, making calculations easier and analyses clearer. This independence is crucial because it allows us to consider interactions and behaviors of various parts of a system without interference from others.
Examples & Analogies
Consider a large assembly of different types of LEGO structures. If each structure represents a different engineering problem, having the ability to work on one structure at a time without worrying about the others fosters creativity and efficiency. When building a complex model, focusing on each structure separately—as if they were parts of a direct sum—enables you to troubleshoot issues in one component without affecting the rest, ultimately leading to a more robust final model.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Direct Sum: A way to express a vector space as a sum of two subspaces U and W, maintaining unique representations.
-
Subspace: A smaller vector space contained within a larger vector space.
-
Decomposition: Splitting a vector space into independent components to simplify problems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: The set of vectors in R³ can be expressed as the direct sum of the xy-plane and the z-axis, as every vector can be uniquely represented with components from each.
-
Example 2: In mechanical systems, complex dynamics may be modeled as the direct sum of translational and rotational motion components.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In spaces combined, the sums we must find, unique is the way, or confusion will stay.
📖 Fascinating Stories
-
Imagine two friends—U and W—who create a dance performance together. They only dance together at the start (the zero vector) but then perform solos that combine into one beautiful act (their unique contributions).
🧠 Other Memory Gems
-
U and W unite, with their unique talents bright—like a perfect sum in sight.
🎯 Super Acronyms
Remember 'USER' for Direct Sums
- Unique
- Sum
- Exclusive
- and Representation.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Direct Sum
Definition:
A direct sum of two vector subspaces U and W is where every element in the vector space V can be uniquely expressed as a sum of elements from U and W, and their intersection contains only the zero vector.
-
Term: Subspace
Definition:
A subset of a vector space that is itself a vector space under the same operations.
-
Term: Decomposition
Definition:
The process of breaking down a vector space into simpler components, typically through the direct sum of its subspaces.