Learn
Games

1.4.3 - Dimensional Analysis

Interactive Audio Lesson

Listen to a student-teacher conversation explaining the topic in a relatable way.

Understanding Dimensional Analysis

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Today, we will explore dimensional analysis, a powerful tool used to convert between different units. Can anyone tell me what they think dimensional analysis might involve?

Student 1
Student 1

I think it has something to do with changing units, like converting inches to centimeters.

Teacher
Teacher

Exactly! Dimensional analysis uses conversion factors, which are relationships between units that allow us to switch from one system to another. For instance, we know that 1 inch equals 2.54 centimeters.

Student 2
Student 2

So if I have 3 inches, how do I convert that to centimeters?

Teacher
Teacher

"Great question! You would multiply 3 inches by the conversion factor, 2.54 cm per 1 inch. Let me show you:

Examples of Dimensional Analysis

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Let's delve into more examples of dimensional analysis. How about we convert gallons to liters? Who knows how many liters are in a gallon?

Student 1
Student 1

I believe 1 gallon is approximately 3.785 liters.

Teacher
Teacher

Great job! Now if we have 5 gallons, how would we convert that to liters?

Student 2
Student 2

You would multiply 5 gallons by 3.785 liters per gallon!

Teacher
Teacher

"Correct! Thus,

Applying Dimensional Analysis

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Now let's practice applying dimensional analysis with problems. Suppose we need to convert 150 mL of a solution to liters. Who can tell me how?

Student 4
Student 4

We can use the fact that 1,000 mL equals 1 L!

Teacher
Teacher

"Exactly! So, we take:

Introduction & Overview

Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.

Quick Overview

Dimensional analysis is a method used to convert units from one system to another using conversion factors.

Standard

This section covers the concept of dimensional analysis, highlighting its significance in converting units using a systematic approach known as the factor-label method. Practical examples demonstrate how to apply this method for unit conversion.

Detailed

Dimensional Analysis

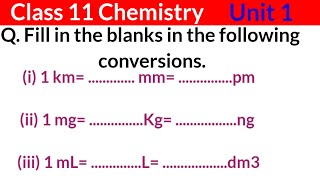
Dimensional Analysis is a vital process in chemistry used to convert units from one system to another by applying conversion factors. This technique, often referred to as the factor-label method, allows chemists to ensure consistency in measurements and calculations across different unit systems. It helps simplify complex conversions and ensures that calculations yield results in the desired units.

Key Points Covered:

  • Definition: Dimensional analysis utilizes conversion factors, which are derived from equivalences between different units, to convert quantities effectively.
  • Examples: The section presents practical examples, such as converting inches to centimeters and liters to cubic meters, to illustrate how to use conversion factors accurately.
  • Process: The dimensional analysis method involves multiplying the measurement by conversion factors in such a manner that the original units cancel out, leaving the desired unit.

This method is foundational in chemistry and various scientific fields, enabling precise calculations and the ability to communicate findings using standardized units.

Youtube Videos

Class 11th Chemistry | Dimensional Analysis | Chapter 1 : Some Basic Concepts of Chemistry
Class 11th Chemistry | Dimensional Analysis | Chapter 1 : Some Basic Concepts of Chemistry
Dimensional analysis by unitary method | Some basic concepts of chemistry | Class 11 Chemistry
Dimensional analysis by unitary method | Some basic concepts of chemistry | Class 11 Chemistry
Dimensional Analysis | Some Basic Concepts of Chemistry | Class 11th | Chapter 1 | Science
Dimensional Analysis | Some Basic Concepts of Chemistry | Class 11th | Chapter 1 | Science
11 NCERT | Ex Solution Q No. 1 | Some Basic Concept of Chemistry
11 NCERT | Ex Solution Q No. 1 | Some Basic Concept of Chemistry
Dimensional Analysis | Easy Trick
Dimensional Analysis | Easy Trick
Class 11 | Ch-1: Some basic concepts of chemistry | Dimensional Analysis
Class 11 | Ch-1: Some basic concepts of chemistry | Dimensional Analysis
Dimensional analysis //class 11th chemistry ||SOME BASIC CONCEPTS OF CHEMISTRY
Dimensional analysis //class 11th chemistry ||SOME BASIC CONCEPTS OF CHEMISTRY
Some Basic Concepts of Chemistry||Class 11 Chemistry||Problem Solved||Dimensional Analysis
Some Basic Concepts of Chemistry||Class 11 Chemistry||Problem Solved||Dimensional Analysis
11th Chemistry Chapter-1 Dimensional Analysis
11th Chemistry Chapter-1 Dimensional Analysis

Audio Book

Dive deep into the subject with an immersive audiobook experience.

What is Dimensional Analysis?

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Often while calculating, there is a need to convert units from one system to the other. The method used to accomplish this is called factor label method or unit factor method or dimensional analysis.

Detailed Explanation

Dimensional analysis is a technique used to convert measurements from one unit to another by using conversion factors. It utilizes the relationships between different units to facilitate the transformation. Whenever you encounter different systems of measurement (like inches to centimeters), dimensional analysis indicates how you can systematically change one to the other without losing accuracy.

Examples & Analogies

Think of dimensional analysis as a language translator for measurements. Just as you might convert English sentences to French while retaining their meaning, dimensional analysis converts units (like inches to centimeters) while maintaining the value of the measurement.

Example of Usage: Converting Inches to Centimeters

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

A piece of metal is 3 inch (represented by in) long. What is its length in cm?

Solution: We know that 1 in = 2.54 cm.

From this equivalence, we can write: Thus, 1/1 in equals 2.54 cm. Both of these are called unit factors.

Detailed Explanation

In this example, you begin with a measurement of 3 inches. By knowing the conversion factor (1 inch equals 2.54 cm), you can create a conversion equation to find the equivalent length in centimeters. Multiplying 3 inches by the conversion factor gives the result in centimeters: 3 in × 2.54 cm/in = 7.62 cm.

Examples & Analogies

Imagine you are buying fabric measured in inches and you need it in centimeters to match your sewing pattern. Using dimensional analysis, you can convert the measurement swiftly, ensuring that you buy exactly the right amount of fabric.

Cubing Units for Volume Conversion

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Say, the jug contains 2L of milk. Calculate the volume of the milk in m³. Since 1 L = 1000 cm³ and 1 m = 100 cm, which gives 1/100³ m³ = 1000000 cm³. To get m³ from the above unit factors, the first unit factor is taken and it is cubed.

Detailed Explanation

In volume calculations, when you convert between liters and cubic meters, you must cube the linear conversion factor because volume is three-dimensional. You know that 1 L equals 1000 cm³. To convert liters to cubic meters, convert liters to cubic centimeters, and then from cubic centimeters to cubic meters, thus applying the conversion factor (1/1000000)³ to account for the three dimensions.

Examples & Analogies

Think of it like filling a swimming pool. If you know the pool can hold 2 liters of water, and you want to change how you measure that (say to cubic meters), you have to consider the length, width, and height—a three-dimensional thinking—which is cubing the original unit factor.

Example of Converting Days into Seconds

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Example: How many seconds are there in 2 days?

Solution: Here, we know 1 day = 24 hours (h) or 1/24 hours/day = 1. Then, 1 h = 60 min or 1/60 hours/minute.

So, for converting 2 days to seconds,
2 days = 2 × 24 × 60 × 60 seconds.

Detailed Explanation

To convert days to seconds, you need to multiply by the conversion factors for days to hours, hours to minutes, and minutes to seconds. Each conversion step gives you a more granular look at the time length. Since there are 24 hours in a day, 60 minutes in an hour, and 60 seconds in a minute, you multiply these unit factors together: 2 days × 24 hours/day × 60 minutes/hour × 60 seconds/minute = 172800 seconds.

Examples & Analogies

Imagine a school bell ringing every hour. If you want to know how many rings the bell makes in a 2-day school event, you could calculate the total hours first (2 days × 24 hours/day), then multiply those hours by the number of rings (the hourly bell ring) to know how many times it rings in total.

Definitions & Key Concepts

Learn essential terms and foundational ideas that form the basis of the topic.

Key Concepts

  • Dimensional Analysis: A systematic method for converting units.

  • Conversion Factor: A ratio used to express how many of one unit is equal to another.

  • Factor-Label Method: A step-by-step approach to unit conversion using multiplication and division.

Examples & Real-Life Applications

See how the concepts apply in real-world scenarios to understand their practical implications.

Examples

  • Converting 3 inches to centimeters using the factor 1 inch = 2.54 cm results in 7.62 cm.

  • Converting 5 gallons to liters utilizing the conversion 1 gallon = 3.785 liters results in 18.925 liters.

Memory Aids

Use mnemonics, acronyms, or visual cues to help remember key information more easily.

🎵 Rhymes Time

  • To convert and be sure, use factors that endure.

📖 Fascinating Stories

  • Imagine a car travels 60 miles in one hour, and you want to know how far it goes in kilometers. Using dimensional analysis, you find the conversion helps you understand distance in metric!

🧠 Other Memory Gems

  • F-L-A-M-E for Factor-Label Analysis: Factor, Label, Apply, Multiply, Endure.

🎯 Super Acronyms

D.A.C. - Dimensional Analysis for Consistency.

Flash Cards

Review key concepts with flashcards.

Glossary of Terms

Review the Definitions for terms.

  • Term: Dimensional Analysis

    Definition:

    A method used to convert units from one system to another using conversion factors.

  • Term: Conversion Factor

    Definition:

    A numerical factor used to multiply a quantity to convert it from one unit to another.

  • Term: FactorLabel Method

    Definition:

    A systematic approach to unit conversion using conversion factors arranged to cancel out unwanted units.

  • Term: Unit Factor

    Definition:

    A ratio that expresses how many of one unit are equal to another unit.