Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Significant Figures
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we're going to learn about significant figures, which are essential for accurately reporting measurements. Can anyone tell me what a measurement means?
It's the size or amount of something we determine using a tool.
Exactly! But every measurement has some uncertainty to it. Significant figures help convey how precise our measurements are. For instance, if I say a length is 2.5 meters, how many significant figures are in that measurement?
That would be two significant figures.
Good job! Letβs remember that by associating significant figures with precision and accuracy in science.
Rules for Counting Significant Figures
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now letβs delve into the rules for counting significant figures. Who can share a rule we've just discussed?
Non-zero digits are always significant!
Right! Can anyone give an example of a number with significant figures?
How about 0.0045? It has two significant figures.
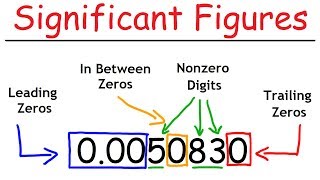
Great! The leading zeros are not counted. Let's summarize these rules so you can remember them easily: Non-zero digits are significant, zeros between significant digits are significant, leading zeros are not significant, and trailing zeros are significant only if there's a decimal.
Significant Figures in Calculations
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's move on to how to handle significant figures in calculations. For addition and subtraction, we use decimal places. Can someone tell me what that means?
The result should have the same number of decimal places as the measurement with the least decimal places.
Exactly! Now, how about for multiplication and division?
The result should have the same number of significant figures as the number with the least significant figures.
Spot on! This ensures we don't misrepresent the uncertainty in our results. Remember the acronym, 'PAM' β precision in addition, and minimum in multiplication.
Precision, Accuracy, and Examples
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's talk about precision and accuracy. What do those terms mean? Can someone offer a distinction?
Precision is how close repeated measurements are to each other, while accuracy tells how close a measurement is to the actual value.
Excellent! For instance, if I weigh an object and get 10.0 g multiple times, that's precise. If it should have been 9.8 g, the measurements are precise but not accurate.
So, we need to ensure both precision and accuracy in our experiments!
Correct! This underscores the importance of significant figures in scientific work.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The concept of significant figures focuses on the precise representation of measurements and the inherent uncertainty in the data. Understanding how to identify significant figures in various types of numbers aids in communicating the accuracy of measurements and performing arithmetic operations correctly.
Detailed
Understanding Significant Figures
Significant figures refer to the digits in a measurement that contribute to its accuracy, including all known digits plus one estimated digit. Every measurement carries uncertainty due to the limitations of measuring tools and methods.
Key Points:
- Definition: Significant figures include all the certain digits in a measurement plus one uncertain digit, indicating the precision of that measurement.
- Rules for Counting Significant Figures:
- Non-zero digits are always significant.
- Any zeros between significant digits are also significant.
- Leading zeros (zeros before the first non-zero digit) are not significant.
- Trailing zeros are significant only if there is a decimal present.
- Operations with Significant Figures: The rules for performing calculations dictate that:
- In addition and subtraction, the result should reflect the least number of decimal places from the calculations.
- In multiplication and division, the result should have no more significant figures than the number with the least significant figures in the calculation.
- Precision vs. Accuracy: Precision indicates the reproducibility of measurements, while accuracy relates to how close a measurement is to the true value.
- Practical Applications: Recognizing significant figures helps ensure clarity and reliability in scientific communication, especially in laboratory settings.
In scientific practice, adhering to the rules of significant figures is paramount for maintaining the integrity of data and results.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Significant Figures
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Every experimental measurement has some amount of uncertainty associated with it because of limitation of measuring instrument and the skill of the person making the measurement. For example, mass of an object is obtained using a platform balance and it comes out to be 9.4g. On measuring the mass of this object on an analytical balance, the mass obtained is 9.4213g.
Detailed Explanation
Significant figures refer to the digits in a number that carry meaningful information about its precision. Each measurement has inherent uncertainty, influenced by the accuracy of the measuring instrument and the skill level of the person taking the measurement. For instance, when we measure the mass of an object using different balances, such as a platform balance and an analytical balance, we might get values like 9.4g and 9.4213g, respectively. The former shows less detail than the latter, which is more precise, because it includes digits that represent smaller increments of mass.
Examples & Analogies
Imagine a chef measuring ingredients for a recipe. If they use a standard kitchen scale, they might determine the weight of flour as 2 cups, which is a rough estimate. Switching to a more precise digital scale could yield a measurement like 476 grams. The first measurement is like the '9.4g' β good for general use but not for precision. The second is similar to '9.4213g,' giving the exact weight needed for a delicate cake recipe, showcasing how careful measurements can alter outcomes.
Counting Significant Figures
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Counting significant figures is essential for reporting scientific measurements accurately. (1) All non-zero digits are significant. (2) Zeros preceding to first non-zero digit are not significant. (3) Zeros between two non-zero digits are significant. (4) Zeros at the end or right of a number are significant, if they are on the right side of the decimal point. (5) Counting the numbers of objects, e.g., 2 balls or 20 eggs, have infinite significant figures as these are exact numbers.
Detailed Explanation
There are specific rules for counting significant figures that help maintain the correct level of precision in measurements. Non-zero digits are always significant (e.g., 285 has three significant figures). Leading zeros (before the first non-zero digit) are not counted as significant. Zeros between non-zero digits count as significant (e.g., 2.005 has four significant figures). Trailing zeros are significant if thereβs a decimal point (e.g., 0.200 has three significant figures, but 100 has only one unless specified differently). Moreover, when counting objects, these whole numbers are considered to have infinite significant figures because they are exact.
Examples & Analogies
Think of a contest where youβre counting candies. If you have exactly 10 candies, that number is precise β itβs like the 'infinite significant figures' situation. However, if you weigh flour on a scale and get 50.0 grams, the decimal point shows precision in measurement. If you wrote 50 grams without the decimal, it would seem less precise. Just like how you would present a carefully crafted essay, your numbers need the same care in reporting!
Precision vs. Accuracy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Precision refers to the closeness of various measurements for the same quantity. However, accuracy is the agreement of a particular value to the true value of the result. For example, if the true value for a result is 2.00 g and student 'A' takes two measurements and reports the results as 1.95 g and 1.93 g. These values are precise as they are close to each other but are not accurate.
Detailed Explanation
In measurements, precision and accuracy are crucial yet distinct concepts. Precision indicates how consistently you can achieve the same result with multiple trialsβmaking sure your data points cluster closely together, irrespective of whether they are correct or not. For instance, if you repeatedly throw darts and they land in the same spot, your precision is high. However, if that spot is far from the intended target, your accuracy is low. Accuracy, on the other hand, indicates how close a measurement is to the actual value or the 'true' amount. In the previous example, student A is getting similar results (high precision), but they arenβt correct (low accuracy).
Examples & Analogies
Consider an archer aiming for a bullseye. If all their arrows hit closely together, they show good precision β it doesnβt matter where they land. If, however, they consistently miss the target, they're not accurate. Now, imagine a second archer whose arrows hit all around the bullseye on different targets. They are accurate since they seem to hit close to the mark, but their precision is poor. Precision and accuracy working together lead to successful measurements, just like strategic playing leads to winning the game!
Rules for Calculating with Significant Figures
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The result cannot have more digits to the right of the decimal point than either of the original numbers. For addition, the sum must have the same number of decimal places as the number with the least decimal places. For multiplication and division, the result has to have the same number of significant figures as the number with the least significant figures.
Detailed Explanation
When performing calculations in scientific contexts, the rules for significant figures guide how we report our results to reflect the measurements' precision. For addition and subtraction, focus on decimal places: the answer can't have more decimal places than the measurement with the fewest. For example, if you add 12.11 + 18.0 + 1.012, the result should be reported to one decimal place, making it 31.1. For multiplication and division, it's about the total number of significant figures: the answer must reflect the one with the least significant figures among your numbers involved. For instance, multiplying 2.5 (two significant figures) by 1.25 (three significant figures) gives you a product rounded to two significant figures: it should come out as 3.1.
Examples & Analogies
Imagine you're baking cookies using a recipe that calls for precise amounts. If you use 1.5 cups of sugar and 2.0 cups of flour, precise ratios matter. If your mixture in some way requires each ingredient calculated right down to the last drop for the cookies to turn out just right, you'd only report the total amount of flour and sugar combined to one decimal place, following the less precise of the two measurements. That's how careful you must be with your data in science β just like chemistry, where each fraction and decimal can make or break the entire outcome!
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Significant Figures: The counting system used to express precision in measurements.
-
Precision: Represents how close multiple measurements are to one another.
-
Accuracy: Indicates how close a measurement is to the true value.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When measuring a length of 2.30 m, there are three significant figures, showing the precision of the measurement due to the trailing zero.
-
For the number 0.00700, there are three significant figures because the leading zeros are not counted but the trailing zeros after the decimal are significant.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Zeros before are a lead, but zeros at the end are a good seed!
π Fascinating Stories
-
Imagine a scientist with two scales, one precise and one approximateβthey always rely on the more accurate scale to communicate their findings clearly.
π§ Other Memory Gems
-
Remember 'NPZ' - Non-zeros are Significant, Zeros between are Significant too!
π― Super Acronyms
SPAM - Significant Figures, Precise Measurement, Accurate Results.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Significant Figures
Definition:
Digits in a measurement that contribute to its precision, including all non-zero numbers, embedded zeros, and trailing zeros in a decimal.
-
Term: Precision
Definition:
The closeness of two or more measurements to each other.
-
Term: Accuracy
Definition:
The closeness of a measurement to the true or accepted value.