Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Aggregate Grading
Unlock Audio Lesson
Today, we're going to delve into an integral part of concrete technology—aggregate grading. Why do you think grading is important for concrete?
I think it helps in making sure the concrete has the right strength and workability.
Exactly! Proper grading minimizes voids and ensures efficient use of materials. One of the mathematical models we use for grading is Fuller's Formula. Does anyone know what that is?
Isn’t it an equation relating the sizes of aggregates?
Yes, it is! Let’s break it down together. The formula is: P = (d^n / D) × 100. Here, P is the percentage passing through sieve size d. Why do you think we express these sizes mathematically?
To calculate the proportions we need for making concrete, right?
Exactly! And using n ≈ 0.5 helps us achieve optimal packing. Remember this as we explore grading further!
Understanding Fuller's Formula
Unlock Audio Lesson
So, let’s explore Fuller's Formula more comprehensively. Who can remind us what the variables represent?
P is the percentage passing, d is the sieve size, and D is the maximum aggregate size.
Correct! And n is the exponent that we adjust based on the desired packing. Can anyone suggest a reason why we might want different values for n?
Different projects might need different strengths or workabilities.
Exactly! And applying this understanding allows engineers to adjust mixes according to specific project requirements. Let's summarize this session. What have we learned today?
We’ve learned about Fuller's Formula to optimize aggregate grading and improve concrete performance.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Fuller's Formula is discussed as a mathematical tool that relates the size of aggregates to the distribution of particle sizes in order to achieve maximum packing density. The section highlights the significance of this method for effective concrete mix design.
Detailed
Detailed Summary
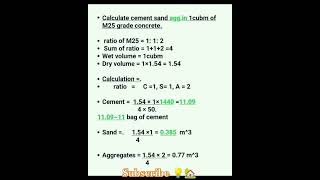
The Mathematical Method (Graphical/Analytical) in concrete aggregate grading focuses on optimizing the combination of particle sizes for effective concrete mix design. The method primarily involves Fuller's Formula, which is mathematically expressed as:
$$ P = \frac{d^{n}}{D} \times 100 $$
Where:
- P = percentage of aggregate passing through sieve size d
- D = maximum aggregate size
- n is typically around 0.5 for optimum packing.
Understanding and applying this formula can help enhance the workability and strength of concrete, ultimately improving the performance and longevity of concrete structures. Consistent adherence to this method allows engineers to fine-tune the granular structure of the aggregate, ensuring minimal voids and optimal bonding with cement paste.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Fuller's Formula Overview
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
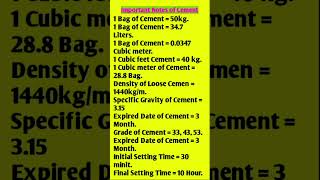
Fuller's Formula:
( d )ⁿ
P = ×100
D
where:
- P = % passing through sieve size d
- D = maximum aggregate size
- n ≈ 0.5 for optimum packing
Detailed Explanation
This formula is used to determine the optimal particle size distribution of aggregates in a concrete mix. It helps ensure that the mix has good packing density, which is essential for achieving the desired strength and workability. Here’s how it breaks down:
- P represents the percentage of aggregate particles that can pass through a specific sieve size, denoted as d.
- D signifies the maximum size of the aggregate particles being used in the mix.
- n is a constant approximately equal to 0.5, which is used for guidelines in achieving optimum packing density.
Overall, the formula indicates that by selecting the right sizes of aggregates, we can enhance the performance characteristics of the concrete.
Examples & Analogies
Think of Fuller's Formula like a recipe for baking cookies. Just as different sizes of chocolate chips (small and large) can affect the overall texture and flavor of cookies, choosing the right sizes of aggregates impacts the strength and workability of concrete. Just as a recipe needs precise measurements to create the best cookies, concrete mix requires the right mix of aggregate sizes to achieve optimal performance.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Fuller's Formula: A mathematical equation used for determining the optimal distribution of aggregate sizes to achieve maximum packing density in concrete mixes.
-
Optimum Packing: The result sought in aggregate grading where particles fit together without unnecessary voids, improving material efficiency.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of concrete mix using Fuller's Formula to compute the gradation required for a specific maximum aggregate size.
-
Application of Fuller's Formula in real-life projects to enhance the quality of construction and concrete durability.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For a mix that's tight and neat, use Fuller's Formula without defeat.
📖 Fascinating Stories
-
Imagine engineers gathering for a project. They discover that the right grading formula helps their concrete stand the test of time, creating a strong structure that benefits the community.
🧠 Other Memory Gems
-
Remember 'Panda Dance' to recall: P = (d^n / D) × 100! The panda represents P, dynamic d, and D for maximum size, like a dance of numbers!
🎯 Super Acronyms
Pigeon Dance
- P: (percentage)
- D: (maximum size)
- d: (sieve size)
- N: (optimum n).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fuller's Formula
Definition:
A mathematical formula used to determine the optimal grading of aggregates in concrete mix design.
-
Term: Aggregate Grading
Definition:
The process of determining the proportions and sizes of aggregate particles in concrete.
-
Term: Optimal Packing
Definition:
The arrangement of particles that maximizes density and minimizes voids in a mixture.