Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Manometers
Unlock Audio Lesson
Today, we'll begin by discussing manometers, a fundamental tool for measuring fluid pressure. Can anyone tell me what a manometer is?
Is it a device that measures pressure using liquid columns?
Exactly! Manometers use liquid columns to balance pressures. Let's remember this with the acronym 'PUMP' - Pressure Using Mercury Piezometers.
How does a simple manometer differ from a U-tube manometer?
Good question! A simple manometer typically measures static pressure while a U-tube manometer can measure pressure differences directly by comparing two liquids' levels. Remember, the difference between heights gives us the pressure in fluid terms!
But how do we know which liquid to use in the manometer?
We usually select liquids of known densities, and the key is that the manometric liquid must have a density suitable for the pressures we expect to measure. Does anyone want to summarize what we discussed?
So, manometers can help us accurately measure pressures by using fluid columns and we must choose liquids wisely based on density?
Exactly! Great recap.
Inclined Manometers and Their Advantages
Unlock Audio Lesson
Now, let's move on to inclined manometers. Can anyone share what they think the benefits of using an inclined design would be?
Maybe they can measure lower pressures more accurately?
Exactly! By inclining the manometer, we extend the measurement length, amplifying the readings even with small pressure changes. Let’s remember this with the mnemonic 'AMP' - Amplified Measurement Precision!
How do we connect the inclined manometer to measure the pressure?
Great question! The basic principle stays the same; we still balance the pressures at the interface of the liquid columns. What's important is to ensure that our reading corresponds to the vertical height projected by the incline.
So we can use trigonometry too, right? Like using sine functions?
Absolutely! The height measurements relate to sin(theta) when resolving the inclined distances. It's a handy relationship for calculations!
Can you summarize the advantages again?
Certainly! Inclined manometers amplify readings making them more sensitive for low pressures, aiding accurate measurements, particularly in various engineering applications.
Differential Manometers and Pressure Differences
Unlock Audio Lesson
Let's discuss the concept of differential manometers. Who can explain the purpose of these devices?
They measure the pressure difference between two points, don’t they?
Right! They focus on the relative pressure rather than absolute. Always remember the phrase 'DIP', which stands for Differential Instead of Pressure!
How do we set them up in a piping system?
You would connect the manometer to two points in the system, ensuring each side is open to measure pressure differences accurately. The setup can involve different fluids in each leg of the manometer.
And what do we do if the fluids are different densities?
Good observation! You would need to account for those densities in your calculations to find the pressure difference. Remember to equate the pressures at their respective interfaces!
Could we summarize the main usage of differential manometers?
Sure! Differential manometers are used to measure pressure differences between two system points, taking into account various fluid densities, which is crucial in understanding system dynamics.
Practical Applications of Hydrostatics
Unlock Audio Lesson
Finally, let's connect our discussion to practical applications. Can anyone think of a real-world structure that utilizes hydrostatic principles?
Stepped wells come to mind because they involve water collection!
Exactly! Stepped wells are a perfect example of how hydrostatics is applied in architectural designs for efficient water harvesting. Think of the acronym 'WELL' - Water Efficiency Leveraged by Levels!
How do these wells remain functional during droughts?
They’re designed to capture and store rainwater efficiently. Canal systems provide a mechanism to keep water levels stable.
So hydrostatic principles are critical in ensuring the sustainability of these systems?
Absolutely! Understanding how pressure and force distributions work enables engineers to create sustainable solutions such as these stepped wells.
Can you recap the main applications we discussed today?
Certainly! We've examined manometers, inclined manometers, and differential manometers, all relating back to hydrostatic principles and their importance in engineering applications like stepped wells.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses the applications of hydrostatics, such as the operation of manometers for pressure measurement, the concepts of differential manometers, and the calculations of forces acting on submerged surfaces. It also highlights the significance of these applications in engineering practices.
Detailed
Detailed Summary
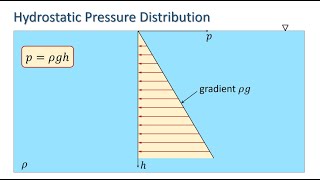
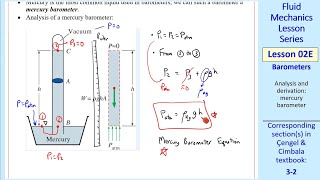
This section delves into the applications of hydrostatics, focusing primarily on two essential tools in fluid mechanics: manometers and inclined surfaces. The discussion begins with a recap of fluid statics, reiterating how pressure varies in fluids at rest, leading to the introduction of manometers as devices to measure pressure differences. The simplest type mentioned is the piezometer, which provides a foundational understanding of pressure measurement in static fluids.
Manometers can be categorized into several types, including U-tube manometers which are commonly used due to their simplicity and accuracy. The section elaborates on the mechanics of how these devices utilize liquid columns to determine pressure differences, specifically referencing the need for density considerations and height measurements of liquid columns for accurate readings.
Moving forward, the text introduces inclined manometers, designed to provide better sensitivity in low-pressure scenarios. The principle of operation is similar to that of conventional manometers; however, with the inclined design, smaller pressure changes can be measured more effectively. The importance of balancing pressures and understanding pressure distributions along submerged surfaces is emphasized.
Additionally, the section touches upon differential manometers, which are essential in scenarios where pressure differences at two points are of interest, as opposed to absolute pressure readings. This concept is particularly relevant to flow measurements in piping systems. The calculations and equations governing these devices underscore their role in engineering applications for pressure monitoring and control.
Lastly, the section hints at practical examples like the stepped well architecture that highlights the historical use of hydrostatic principles in engineering design.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Hydrostatic Applications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In the last class we derived the pressure force acting on the fluid and discussed how hydrostatic pressure varies along the z direction. We simplified problems so that on a horizontal surface, the pressure becomes constant. We are now going to explore two applications of hydrostatics: manometers and inclined surfaces.
Detailed Explanation
In fluid mechanics, hydrostatic pressure refers to the pressure exerted by a fluid at rest. We learned that when examining fluids at rest, the pressure at a horizontal surface remains constant. Now, we are going to apply this knowledge to two real-world applications: manometers, which help us measure pressure, and the analysis of pressure on inclined surfaces. Understanding these concepts is critical in fields like engineering and meteorology, where accurate pressure measurements are essential.
Examples & Analogies
Think of a manometer as a special water level indicator used in plumbing. Just like how a water level in a tank shows how full it is, a manometer measures the pressure of water flowing through pipes. This is similar to how a gauge on your car's dashboard shows how much fuel is left.
Understanding Manometers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Manometers are simple devices used to measure pressure by using a liquid column. A typical manometer can be vertical, inclined, or U-shaped. The simplest form is a piezometer, which measures pressure directly from a liquid column height.
Detailed Explanation
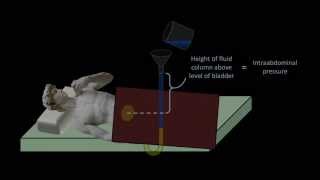
A manometer measures pressure by balancing the weight of a liquid column against the pressure of the fluid being measured. For instance, in a piezometer, the height of the liquid column correlates directly to the pressure within a pipe. If we know the density of the liquid and the height of the liquid column, we can calculate the pressure easily using hydrostatic principles. The measurement will reflect the pressure acting on the system allowing engineers to ensure safe and efficient fluid transport.
Examples & Analogies
Imagine using a straw to drink lemonade. If you cover the top of the straw with your thumb, the lemonade doesn't fall out even when you take it out of the glass. The pressure of the atmosphere is holding the lemonade up. A piezometer works similarly. The height of the lemonade in the straw tells you how much pressure is there.
Inclined Manometers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Inclined manometers are advantageous as they amplify pressure readings, making them suitable for low pressures. The inclination increases the measured distance, enhancing sensitivity.
Detailed Explanation
Inclined manometers are designed to measure low pressures more accurately. By tilting the measuring tube, the height difference due to pressure can be measured more easily than in a vertical manometer. The longer length of liquid column increases the sensitivity, allowing small pressure changes to be detected which could be critical in certain applications like laboratory measurements.
Examples & Analogies
Think of it like using a long ruler instead of a short one to measure a length. A longer ruler allows for more precise measurement of shorter lengths. Similarly, an inclined manometer gives more precise readings for low pressures by stretching the height difference over a longer distance.
Differential Manometers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Differential manometers measure pressure differences between two points in a fluid system, focusing on relative pressure rather than absolute.
Detailed Explanation
In many cases, knowing the difference in pressure between two locations is more critical than knowing the absolute pressure at those points. Differential manometers serve this purpose by connecting two points in a fluid system and measuring the resulting height difference of the fluid column. This type of manometer allows us to determine how much pressure is driving fluid from one place to another, which is crucial in various engineering applications.
Examples & Analogies
Consider two water tanks connected by a pipe. If one tank is higher than the other, water will flow from the higher tank to the lower one. A differential manometer measures the difference in water levels in two connected tubes, telling us how quickly water will flow between the tanks, similar to how we might gauge the strength of a flow of water through a garden hose.
Micro Manometers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Micro manometers are designed for measuring small pressure differences and often include a mechanical arrangement to facilitate measurement and calibration.
Detailed Explanation
Micro manometers are precision instruments used to measure very small pressure changes in fluids. They typically feature a reservoir and flexible tubing, and are calibrated using a screw mechanism that allows for fine adjustments and readings. This level of precision is useful in various applications, from laboratory research to industrial processes, where even minor variations in pressure could have significant implications.
Examples & Analogies
Imagine using a finely tuned scale to weigh small amounts of spice when cooking. Just as the precise scale can make a big difference in flavor, a micro manometer helps ensure accurate pressure readings in sensitive systems, ensuring that processes operate smoothly and efficiently.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Manometers: Devices used for measuring pressure differences in fluids using liquid columns.
-
Inclined Manometers: Offer better accuracy for low-pressure measurements due to their design.
-
Differential Manometers: Measure pressure differences between two points in a fluid system rather than absolute pressures.
-
Hydrostatic Pressure: The pressure exerted by a fluid at rest, with variations based on depth and density.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The use of a U-tube manometer to measure the pressure of a liquid in a pipe system.
-
Differential manometers are employed in industrial settings to monitor the pressure difference in flow systems.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Manometers balance to show you the press, in columns of liquid, they'll assess!
📖 Fascinating Stories
-
Imagine a fluid sitting still in a pond. A tiny manometer dips its end, measuring how much pushes on the liquid - whether near the bank or deeper in!
🧠 Other Memory Gems
-
DIP - Differential Instead of Pressure to remember that differential manometers focus on pressure differences!
🎯 Super Acronyms
AMP - Amplified Measurement Precision to recall the benefits of inclined manometers for accurate low-pressure readings.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Manometer
Definition:
A device used to measure pressure differences by using liquid columns.
-
Term: Pressure
Definition:
The force applied perpendicular to the surface of an object per unit area.
-
Term: Hydrostatics
Definition:
The study of fluids at rest and the forces and pressures associated with them.
-
Term: Differential Manometer
Definition:
A type of manometer used to measure the pressure difference between two points in a fluid system.
-
Term: Inclined Manometer
Definition:
A manometer whose main scale is set at an angle, allowing for more precise measurements of low pressures.