Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Manometers
Unlock Audio Lesson
Welcome, class! Today, we'll begin discussing manometers, devices used to measure fluid pressures. Can anyone tell me what they think a manometer does?
I think a manometer measures the pressure in fluids, right?
Exactly! Manometers can measure the pressure exerted by liquid columns. They're crucial in fluid mechanics.
What kinds of manometers are there?
Great question! The simplest forms include piezometers and U-tube manometers, which we will discuss later. Remember the acronym PU — Piezometer and U-tube!
What’s the difference between those two?
A piezometer measures pressure at a single point, while a U-tube can measure the pressure difference between two points. It’s essential to note these functionalities!
So, does every manometer type serve the same purpose?
Not quite! Each type has specific applications depending on the situation, and we'll cover that as we go. Let's move on to the differential manometer.
Understanding Differential Manometers
Unlock Audio Lesson
Differential manometers are designed to measure the pressure difference between two points rather than absolute pressures. Student_1, what can you tell me about how they work?
They probably compare the heights of two fluid columns, right?
Exactly! By measuring the height difference of the fluid columns and applying hydrostatics, they provide a pressure difference reading. Let’s discuss an equation that represents this relationship!
What does that equation look like?
The equation is: \(P_A - P_B = \rho_{manometric} g (h_1 - h_2)\). It relates pressure difference to the height of the liquid columns, and \(\rho\) is the liquid's density. Can anyone summarize that equation?
If I remember, it's about how pressure difference changes the height of liquids in the manometer!
That’s a perfect summary! Remember, understanding this principle helps us analyze many fluid systems.
Applications of Differential Manometers
Unlock Audio Lesson
Now let’s discuss where we use differential manometers in real life. Student_2, can you think of any practical applications?
Maybe in industrial piping systems to monitor flow rates?
Absolutely! They're common in various industries to measure pressure differences in pipelines. It helps in understanding flow behavior. Can you think of any other scenarios?
How about in laboratories for experiments involving liquids?
That's right! They’re great for experimentation in labs as well. Just remember: differential manometers focus on pressure differences, which are vital in many applications!
What benefits do these give compared to things like a regular pressure gauge?
Great inquiry! Unlike gauges that measure absolute pressure, differential manometers allow us to focus on the pressure differences, which are often more insightful for system dynamics.
Comparative Analysis of Manometer Types
Unlock Audio Lesson
Let’s compare differential manometers to other types. What do you think makes them special compared to piezometers? Student_3?
Piezometers are for single-point readings, right? So, differential manometers give more information.
You're right! While piezometers measure absolute pressure, a differential manometer provides us with insights about flow differences. Student_4, can you think of another type we might compare?
Inclined manometers seem useful, especially for low pressure!
Good observation! Inclined manometers are indeed preferred in low-pressure scenarios due to their enhanced readability. Remember: 'Low Pressure, Be Inclined' — that’s a tip to remember their special application!
Recap and Summary of Differential Manometers
Unlock Audio Lesson
Before we finish, let's recap our discussion about differential manometers. Student_1, can you summarize the key points?
Differential manometers measure pressure differences, use liquid columns to find height, and help in applications like pipeline monitoring.
Fantastic summary! Remember that they focus on the difference rather than absolute pressures, and we can apply this knowledge in various situations. How about a quick pop quiz before we end?
Yes, let’s test our understanding!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The differential manometer measures the pressure difference between two points, making it essential in fluid mechanics. This section details its function, types, and applications, including comparisons with other manometer types such as piezometers, U-tubes, and inclined manometers.
Detailed
Differential Manometer
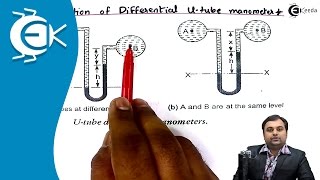
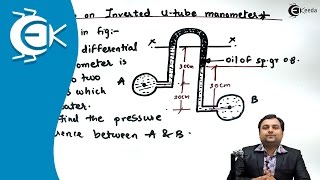
A differential manometer is a device used to measure the pressure difference between two points in a fluid system, which is critical in various applications such as pipe flow. Unlike absolute pressure measurements, differential manometers focus on the relative pressure between two points, which allows for a better understanding of fluid dynamics in systems where pressure differences drive flow.
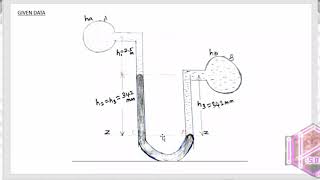
Differential manometers typically consist of a U-tube filled with a manometric fluid, which can be any suitable liquid such as water or mercury. The key here is to measure the height difference of the fluid columns corresponding to the pressure difference at the points of interest.
The operation of differential manometers relies on hydrostatic principles, as pressure differences cause variations in the height of liquid columns. The balance of pressures at two points can be established using the equation:
$$P_A - P_B = \rho_{manometric} g (h_1 - h_2)$$
where \(P_A\) and \(P_B\) are the pressures at two points, \(\rho_{manometric}\) is the density of the manometric fluid, and \(h_1\) and \(h_2\) are the heights of the fluid columns on either side of the manometer.
This section also compares different types of manometers such as piezometers, U-tube manometers, and inclined manometers, focusing on advantages and appropriate usage scenarios. The practical implications of differential manometers are vast, from measuring differences in pressure for flow monitoring in industrial applications to their role in laboratory setups.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Differential Manometers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Differential manometers measure the difference of pressure between two points in a fluid system. They do not measure the actual pressures at any point but rather the pressure difference which drives the fluid flow from one point to another.
Detailed Explanation
A differential manometer is a device that helps us understand how pressure varies between two points in a fluid system. It's not concerned with what is happening at each point alone but rather how different or similar the pressure is between the two points. For example, in a pipe system, if we want to know how much pressure is causing water to move, we would use a differential manometer attached at those two points. This way, we can calculate the difference that is influencing the flow.
Examples & Analogies
Imagine you are at two ends of a water slide. The higher the slide on one end compared to the other, the faster you will slide down because of the difference in height. Similarly, in a fluid system, where we have different pressures at two points, the fluid moves from high pressure to low pressure, much like you sliding down from high to low.
Setup of the Differential Manometer
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The manometer typically consists of a U-tube connected to two points in a piping system where the pressure difference is to be measured. Each side of the U-tube may contain different types of liquids with varying densities.
Detailed Explanation
In setting up a differential manometer, you have a U-shaped tube filled with a liquid that can measure pressure changes. The ends of the tube are connected to the two different locations in the piping system. When the fluid in the pipe experiences a pressure difference, the liquid in the U-tube will rise or fall in response to those pressures. The difference in height of the liquid in the U-tube gives us a measurable value that corresponds to the pressure difference.
Examples & Analogies
Think of a barometer that measures atmospheric pressure. If one end of a U-tube is submerged in a pipe with water and the other end is open to the atmosphere, the difference in liquid heights shows how much pressure is in the pipe versus the atmospheric pressure outside. It’s like two people on a seesaw; when one person pushes down, the other goes up, indicating their respective sides' difference.
Equating Pressures
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To determine the pressure difference using the differential manometer, we can equate pressures at different points along the fluid surfaces, applying the principles of hydrostatics.
Detailed Explanation
To compute the pressure difference, we apply the hydrostatic equilibrium condition. This means that at the same horizontal level in a static fluid, the pressure is the same. By measuring the heights of the liquid columns in the U-tube at both points, we can equate the pressures and find the difference based on the fluid densities and the heights measured.
Examples & Analogies
Imagine holding a still water balloon while you’re underwater. Regardless of where you poke the balloon, the pressure inside the balloon is consistent. Similarly, in this situation, we’re using the consistent pressure levels at equivalent heights in the manometer to calculate the pressure difference, allowing us to determine how much pressure is driving the flow.
Applications of Differential Manometers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Differential manometers are used in various applications, especially in industries where pressure difference measurements are crucial for processes like lubrication systems, chemical processing, and fluid transport.
Detailed Explanation
In industry, knowing the pressure difference between different points in a fluid system is critical for safety and efficiency. Differential manometers can help engineers assess how well a fluid is flowing, whether it's oil in a lubrication system or water in a chemical processing plant. By measuring these differences, they can optimize operations and detect any potential issues before they become critical.
Examples & Analogies
Consider a car's engine oil. To ensure everything runs smoothly, the oil pressure must be appropriate. A differential manometer in the lubrication system can provide real-time data about pressure differences, helping mechanics understand if the system is working correctly and allowing them to catch and fix issues before they lead to engine failure, similar to a doctor checking your blood pressure to catch any health issues early.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Differential Manometer: A device measuring the pressure difference between two points.
-
Piezometer: A simpler form measuring absolute pressure.
-
Hydrostatic Principle: Pressure difference is measured based on liquid column heights.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In an industrial setting, differential manometers are employed to monitor the pressure drop across filters in a fluid filtration system.
-
In laboratories, these devices measure the pressure required in chemical processes, thus indicating the operational efficiency of experiments.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To find the pressure difference, don’t go far, measure the heights, that's the real star!
📖 Fascinating Stories
-
Imagine a small village where citizens lose water pressure every summer. A smart engineer introduces a differential manometer to measure and optimize the pressure difference, reviving the village’s water flow.
🧠 Other Memory Gems
-
D.P.M. stands for Differential Pressure Measurement — a reminder that these measure differences, not absolutes.
🎯 Super Acronyms
Remember 'D.M. for D.P.' - Differential Manometer stands for Differential Pressure.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Differential Manometer
Definition:
A device that measures the pressure difference between two points in a fluid system.
-
Term: Piezometer
Definition:
A device used to measure the static pressure at a single point in a fluid.
-
Term: Utube Manometer
Definition:
A device used to measure pressure differences using a U-shaped tube filled with liquid.
-
Term: Inclined Manometer
Definition:
A type of manometer that is inclined to amplify pressure readings, especially for low pressures.
-
Term: Hydrostatic Pressure
Definition:
The pressure exerted by a fluid at rest due to the force of gravity.