Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Basics of Hydrostatic Pressure
Unlock Audio Lesson
Today, we are going to discuss hydrostatic pressure. Can anyone tell me what hydrostatic pressure is?
Isn't it the pressure exerted by a fluid at rest due to the force of gravity?
Excellent, Student_1! To remember this, think of it as 'Hydro in rest, gravity's best.' Hydro means water, and static refers to rest. Now, how does this pressure change with depth?
I believe pressure increases as we go deeper into the fluid?
Yes, that's right! The pressure at a certain depth can be calculated using P = P_atm + ρgh. Makes sense?
So, if the height increases, pressure also increases?
Exactly! Remember that pressure is caused by the weight of the fluid above, and it acts equally in all directions. Let's summarize this: hydrostatic pressure increases linearly with depth due to gravity.
Manometers and Their Applications
Unlock Audio Lesson
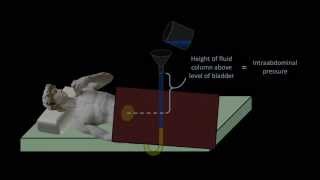
Next, let's delve into manometers. Who can describe what a manometer is?
A manometer measures the pressure of a fluid column based on the height of the liquid in the tube?
Great job, Student_4! Think of manometers as tools that balance pressure across a column of liquid. Can someone mention a type of manometer?
There’s the U-tube manometer, right?
Yes! The U-tube manometer can measure pressure differences between two points. How do we use it?
We calculate the difference in heights of the fluid in the two arms to find the pressure difference.
Exactly! Remember this formula: P = ρg(h_1 - h_2). Now, what are the advantages of using an inclined manometer?
It provides a greater sensitivity for measuring low pressures, right?
Correct! The incline amplifies small changes in height. Let's wrap this session: manometers serve as essential tools in fluid mechanics for pressure measurement, adapting their designs based on the context.
Differential Manometers: Understanding Pressure Differences
Unlock Audio Lesson
Now, let's discuss differential manometers. Does anyone know what makes them different?
They measure the pressure difference between two points in a fluid system!
Exactly! Think of them as 'difference detectors.' How do we set it up?
You connect it to two different points of the fluid system and measure the height difference.
Perfect! And why do we prefer them over standard manometers in many cases?
Because sometimes we need to know just how much pressure difference is driving the flow, not the absolute pressure.
Absolutely! Remember, 'differentiate to elevate your understanding of fluid flow.' So let's summarize: differential manometers help us assess the pressure difference necessary for flow.
Practical Application: Stepped Wells
Unlock Audio Lesson
Finally, let's look at a real-world application—stepped wells. Does anyone know their purpose?
Yes, they are designed for rainwater harvesting!
Correct! They ensure water availability even during droughts. How do hydrostatic principles apply here?
The pressure at different depths helps manage water levels efficiently.
Absolutely! The design leverages hydrostatic pressure to allow users to access water at different levels easily. Let’s summarize: stepped wells exemplify the application of theoretical fluid mechanics in solving practical engineering problems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section introduces key concepts in fluid statics, particularly hydrostatic pressures and how they are measured using devices like manometers. It elaborates on the theory behind these measurements and provides examples, including differential manometers and the significance of hydrostatic forces on submerged surfaces.
Detailed
In this section on 'Measurement of Pressure and Hydrostatic Forces,' we delve into the principles of fluid statics and measurement. It starts with a recap of hydrostatic pressure distributions, emphasizing how pressure depends on depth in a fluid, consistent with Pascal's law. The section elaborates on different types of manometers including piezometers, U-tube manometers, and inclined manometers, explaining their roles and applications in measuring pressure differences in fluid systems. It highlights the importance of understanding fluid density, height differences, and how these factors affect pressure readings. The discussion also extends to the measurement of differential pressures between two points, especially in pipe systems using differential manometers. Finally, it provides practical insights into submerged surfaces and examples of applications like stepped wells, underpinning the concepts with real-life applications in civil engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Fluid Statics and Pressure Measurement
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Welcome to this lecture on fluid mechanics. As we discussed in the last class fluid at rest and fluid statics we have derived basic equations of fluid statics. That is what the pressure equations with related to gravity field. So now, just we will have a two applications of the fluid at rest or hydrostatic pressure distributions that what I will address as a applications to two cases.
One is manometer. Another is for a inclined surface, a somewhat inclined surface what could be the pressure distributions, what could be the total pressure force acting on that plane, also the center of pressure.
Detailed Explanation
In this section, the focus is on fluid statics, which studies fluids at rest. The fundamental concept discussed here is the measurement of pressure due to gravity acting on a fluid column. Two applications of hydrostatic pressure are introduced: the manometer, a device used for measuring pressure, and scenarios involving inclined surfaces and their pressure distributions.
Examples & Analogies
Imagine a tall glass filled with water. The pressure at the bottom of the glass is higher than at the top because of the weight of the water above it. Similarly, if you were to use a manometer to measure the water pressure at the bottom of the glass, it would reflect the gravitational effects on that column of water.
Manometer Types and Functionality
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us come to the manometer. Very simple devices are used to measure the pressure like you have a, let have these type of conduit, the pipes the carrying any liquids and you want to measure it what could be the pressure on that pipe. So we can just insert the tubes like you can see can have the tube like this or can have a tube like this with inclined and all or you can have a inclined like this.
So each one having the merit and also disadvantage, like for examples, the manometer is simple device that is what use a liquid column to measure the pressure between two points okay.
Detailed Explanation
This chunk explains what a manometer is and how it functions. A manometer is a device that uses a column of liquid to measure the pressure difference between two points. Different types of manometers include vertical, inclined, and U-tube types. Each variation has its own advantages and disadvantages depending on the application, including measuring liquid pressures in pipes.
Examples & Analogies
Think of a manometer as a playground slide. Depending on the incline of the slide, the way kids (representing pressure) move down will vary. A steeper slide (inclined manometer) could help kids reach the bottom faster (indicating higher pressure), while a gentle slide (U-tube manometer) allows for a more gradual descent.
Measurement Techniques with Manometers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Similar way you can have a inclined one or just a vertical one or the having this concept of the half rectangular case. See if you look it that in case of the inclined one that if I have the inclined length is l that means the height of the liquid rest is h is proportional to sinθ. ... You can see here that the incline helps to amplify the pressure reading.
Detailed Explanation
Here, the text discusses how the geometry of the manometer (inclined versus vertical) affects the pressure readings. An inclined manometer allows for easier readings especially for low pressures. The height of the liquid column in inclined manometers is proportional to the sine of the angle of inclination, amplifying the measured pressure differences.
Examples & Analogies
Imagine trying to read a ruler laid flat versus one that's tilted. When tilted (like an inclined manometer), you might get a broader scale that helps you see smaller increments of measurement more clearly. This helps when you're measuring low liquid levels.
Differential Manometers and Their Application
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now there is another type of manometer which is called the differential manometers. As the name says that here, we do not measure a particular point pressure measurements where you consider two points. ... I want to looking for a relative pressure between these two difference between these two points of A and B in this pipe flow.
Detailed Explanation
Differential manometers are specialized devices used to measure the pressure difference between two points instead of measuring each point's absolute pressure. This becomes significant in applications where the difference in pressure drives fluid flow, such as in pipes. The comparison allows engineers to determine how effectively fluids are moving through systems.
Examples & Analogies
Imagine you're examining two adjacent hoses with water flowing through them. A differential manometer acts like a teacher comparing the flow rates of each hose to see which one is applying more force. By evaluating the difference in pressure, you can figure out how the water is moving across the system.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatic Pressure: The pressure exerted by a fluid at rest due to gravity, increasing with depth.
-
Manometer: An instrument used to measure fluid pressure through the height of a liquid column.
-
Differential Manometer: Measures the difference in pressure between two points in fluid systems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using a U-Tube Manometer to measure pressure in a pipeline.
-
Employing an inclined manometer in a wind tunnel to measure low pressure differences.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Hydrostatic pressure, takes the fluid's weight, deeper you go, the greater the rate.
📖 Fascinating Stories
-
Imagine a deep well where the water pressure rises as you go lower. The farther down you reach, the heavier is the water above, reminding you of hydrostatic principles.
🧠 Other Memory Gems
-
Remember 'MDI' for Manometer, Differential, Inclined - key types we discussed.
🎯 Super Acronyms
The acronym 'PHD' helps to remember Pressure, Height, Depth in context of hydrostatics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatic Pressure
Definition:
The pressure exerted by a fluid at rest due to the force of gravity at a specific depth.
-
Term: Manometer
Definition:
A device used to measure the pressure of a fluid by balancing it against a column of liquid.
-
Term: UTube Manometer
Definition:
A type of manometer consisting of a U-shaped tube filled with liquid, used to measure pressure differences.
-
Term: Differential Manometer
Definition:
A manometer that measures the pressure difference between two points in a fluid system.
-
Term: Inclined Manometer
Definition:
A manometer designed with an incline to enhance the sensitivity for measuring low pressures.