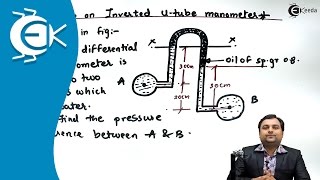
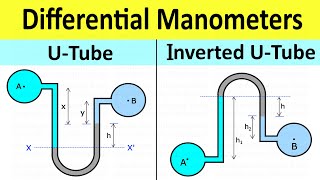
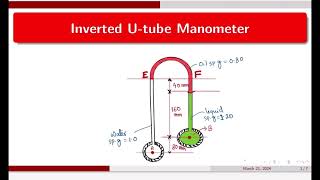
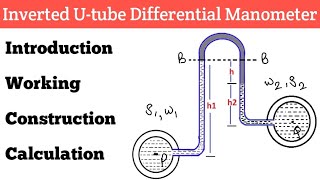
Inverted U Tube Manometer
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Manometers
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we’re exploring manometers, specifically the inverted U-tube type. Can anyone tell me what a manometer is?

A manometer is a device used to measure pressure!

Exactly! Manometers measure pressure by comparing the heights of liquid columns. What happens if the manometric fluid is lighter than the working fluid?

We have to account for that in our calculations!

Great point! Remember to adjust our pressure equations to reflect this. Let’s delve deeper into how to use these formulas effectively.
Calculating Pressure with Inverted U-Tube Manometers
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

"When calculating the pressure in an inverted U-tube manometer, we primarily use the equation: P = P_{atm} +
Applications of Inverted U-Tube Manometers
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Inverted U-tube manometers are used widely. Can anyone provide an example of where they might be applied?

They are used in laboratories for measuring pressure differences in experiments.

That’s one! They’re also used in industries like oil and gas to monitor pipeline pressures. Why is this important?

It helps prevent leaks and maintain system integrity.

Exactly! Monitoring pressures ensures safety and efficiency in fluid systems.
Understanding Pressure Dynamics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

So, what happens to our pressure readings if our working fluid is denser than our manometric fluid?

We would have to use a different formula to account for the greater pressure.

Correct! The sign and density will significantly impact our calculations. Let’s practice applying these to sample problems.

Are there common errors to watch out for when doing these calculations?

Absolutely! Mistakes often arise with sign conventions, so always verify your positive and negative placements in the equations.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section focuses on the inverted U-tube manometer, a device used for measuring pressure differences between two points in a fluid system. It explains the conditions under which it operates, including the use of lighter manometric fluids than the working fluid, and highlights key calculations involved in determining pressure based on liquid densities and height differences.
Detailed
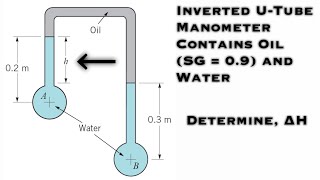
Inverted U-Tube Manometer
The inverted U-tube manometer is a common fluid measurement instrument designed to determine pressure differences between two fluid points in a system. Unlike traditional manometers, this variant utilizes lighter manometric fluids compared to the working fluid, leading to unique operational dynamics.
In essence, pressure is measured by the height difference of the liquid columns in the arms of the tube, correlating with the pressures at the measurement points. When using a lighter manometric fluid, it is crucial to remember that pressure calculations must account for the fluid density differences. The mathematical concept involves equations like
$$ P = P_{atm} +
ho_{m}gh $$
for the pressure in the working fluid, and similarly for the manometric side, taking signs into account due to the fluid column's orientation. This structure allows engineers and researchers to measure subtle pressure differences effectively, showcasing the utility of inverted U-tube manometers in various applications, including pipelines, wind tunnels, and laboratory settings. The understanding of these principles is essential for anyone studying fluid mechanics.
Youtube Videos





Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Inverted U Tube Manometer
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now if you look it if I have a inverted U tube okay that is inverted cases okay, this is the meter. When you use the manometer fluid use in this type of manometer is lighter than the working fluids. So these are two are the working fluid, which is having this density and at two different density of the working fluid. But is the density of the manometric fluid. And here this manometric fluids having the lighter than the working fluid. That means the is less than and is less than the .
Detailed Explanation
The inverted U tube manometer is a device used to measure the pressure difference between two points in a fluid system. In this manometer, the manometric fluid used is lighter than the working fluids. This means that the density of the manometric fluid is less than the densities of the working fluids being compared. The inverted configuration allows for a greater measurement range in applications where the working fluid's pressure is light compared to the manometric fluid. Essentially, it captures the pressure differences effectively by allowing for fluid movement in the U-tube and displaying a height difference that correlates with pressure.
Examples & Analogies
Imagine you have two connected syringes, one filled with a thick liquid (like syrup) and the other with a lighter liquid (like water). When you apply pressure to the thick liquid, it might push the lighter liquid up the tube, creating a visible height difference. This concept mirrors how the inverted U tube manometer works, visually representing pressure differences based on fluid heights.
Pressure Measurement Basics
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So in case of a U tube manometer which is inverted one then we use the same equations. Only these negative terms are comes it the because it is a U tube inverted one. We go off to measure the pressures on that surface as compared to the working fluid which is a lower than that.
Detailed Explanation
In an inverted U tube manometer, the same basic pressure measurement equations are used as in a regular U tube manometer. However, since the manometer is inverted and the manometric fluid is lighter, we often need to consider negative pressure contributions when calculating overall pressure based on the fluid column heights. This is due to the orientation of the fluid; when the fluid is forced up, it contrasts against the gravitational pull, and we factor this into our equations. Thus, recognizing the orientation informs the signs used in calculations.
Examples & Analogies
Think of this like balancing a seesaw. When one side goes up, the other side goes down. If you were to measure the height of the seesaw on either end and account for which side is heavier, you would adjust your expectations for how high the lighter side rises. Similarly, in a manometer, when measuring pressure, you account for the lighter manometric fluid's behavior opposite the heavier fluid.
Pressure Calculations in Inverted U Tube Manometer
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So you can write this pressure equations for a inverted U tube manometers considering this is the surface where you are equating the pressure which is you can consider any other location that does not matter it.
Detailed Explanation
To derive the pressure equations for the inverted U tube manometer, we establish a reference surface where pressures can be equated. The fundamental idea is that pressure is uniform across any horizontal surface when fluids are at rest. Therefore, by selecting a suitable reference point in our equation, whether at the bottom of the U tube or elsewhere, we can formulate an equation to relate the fluid heights and densities. This flexibility in choosing reference points allows for different configurations and easier calculations.
Examples & Analogies
Consider a water balloon that is evenly filled. Regardless of where you press on the balloon, the water redistributes to maintain a consistent pressure throughout. Similarly, in an inverted U tube manometer, we can choose any convenient level as our reference point for pressure measurement as fluid pressure remains equal at any level in the connected body of water.
Understanding Fluid Density Relationships
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So when you have to consider this point it does not matter it, you can solve the problems. But you need to a sign conversion whether these working fluid, the positive and negative sign of h you can consider to solve the problems.
Detailed Explanation
In solving problems involving inverted U tube manometers, it's crucial to understand the relationships between different fluid densities. When setting up equations, the densities of the manometric fluids and the working fluids impact the calculations significantly. Engaging with sign conventions becomes essential as pressures can be described positively or negatively depending on whether the fluid height increases or decreases relative to the expected baseline. A methodical approach in determining these signs ensures accuracy in the pressure computations.
Examples & Analogies
Think about a scale measuring weight. If you add weight to one side of the scale, it tips down, indicating a positive increase on that side. Conversely, if you remove weight, it tips back up, signaling a negative weight change on that side. In the same way, when using an inverted U tube manometer, we gain insight into how adding or subtracting fluid heights yields positive or negative pressure readings.
Key Concepts
-
Pressure Measurement: Understanding how liquid columns can be used to determine fluid pressure.
-
Inverted U-Tube Structure: The concept of measuring pressure with a U-tube where the manometric fluid is lighter.
-
Pressure Equations: The mathematical relationship expressing how pressure is calculated from height difference, fluid density, and gravity.
Examples & Applications
Example 1: Using an inverted U-tube manometer to measure the pressure in a natural gas pipeline.
Example 2: Adjusting the readings of a manometer when the manometric fluid density is known to be less than the working fluid density.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Pressure's height, in fluid's flow, helps us see just how it goes!
Stories
Once in a lab, a curious student found an old U-tube manometer. They discovered how by looking at the fluid heights, they could measure the pressure in pipes. They realized sharing this story would help others understand the power of keeping grades up—just like measuring pressures helped monitor vital systems!
Memory Tools
Remember the acronym PHAZE: P for Pressure, H for Height, A for Atmosphere, Z for Zero net change, E for Equilibrium in the liquid phases.
Acronyms
DAMP
Density
Atmospheric pressure
Manometer fluid
Pressure – key components in understanding manometer calculations.
Flash Cards
Glossary
- Manometer
A device used to measure pressure by comparing the heights of liquid columns.
- Utube Manometer
A type of manometer that consists of a U-shaped tube filled with a liquid used to measure pressure differences.
- Manometric Fluid
The liquid used in a manometer to measure pressure differences.
- Density (ρ)
The mass per unit volume of a substance, often used in pressure calculations.
- Hydrostatic Pressure
The pressure exerted by a fluid at rest due to the weight of the fluid above.
Reference links
Supplementary resources to enhance your learning experience.
