Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Manometers
Unlock Audio Lesson
Today, we will learn about manometers, specifically inclined manometers. Can anyone tell me what a manometer does?
A manometer measures the pressure of a liquid, right?
Exactly! Manometers measure the pressure difference between two points. They use a liquid column to do this. Remember, pressure is related to the height of this column due to hydrostatic principles.
What is hydrostatic pressure?
Great question! Hydrostatic pressure is the pressure exerted by a fluid at rest. It increases with depth and is influenced by the fluid's density and gravitational force. Let's remember that with the acronym 'HAP' - Hydrostatic, At rest, Pressure.
How does the inclination of the manometer help in measuring pressure?
When we incline a manometer, we increase the effective length of the liquid column, which enhances sensitivity to low pressure changes. This means even small pressure differences can be accurately measured.
So we can use an inclined manometer for measuring levels in low-pressure systems?
That's right! Always remember, inclined manometers amplify readings, making them excellent for low-pressure applications. To recap, manometers measure pressure by assessing the height of a liquid column, and inclination enhances their sensitivity.
Understanding Pressure Measurement
Unlock Audio Lesson
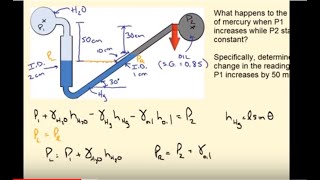
Let’s look at how to actually calculate pressure using an inclined manometer. If we have two liquids of different densities, how do we set up our equations?
Do we need to consider the difference in densities?
"Absolutely! The pressure at a certain height is determined by both the density of the liquid in the manometer and the density of the liquid in the pipe. Remember the formula:
Applications of Differential Manometers
Unlock Audio Lesson
Differential manometers measure the difference in pressure between two points. Can anyone explain why someone would want to measure pressure differences specifically?
To understand how a fluid is flowing, I guess? Like, to measure flow rates?
Exactly! Knowing the pressure difference helps us analyze flow characteristics and ensure that systems operate efficiently. Differential manometers can handle different fluid densities too, which is helpful in industrial applications.
So how do we calculate the pressure difference?
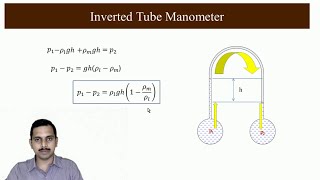
"You would set the pressures at both points equal, considering the density of fluids and their respective heights. It results in a simplified equation:
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Inclined manometers are essential tools in fluid mechanics for measuring pressure differences in various applications. This section delves into their operation, the importance of hydrostatic principles, and demonstrates their functionality through various examples, including differential manometers.
Detailed
Detailed Summary
Inclined manometers are devices utilized to measure fluid pressure by using a liquid column. They function based on hydrostatic principles, allowing us to determine the pressure difference between two points in a fluid system. The inclination of the manometer amplifies the response to low pressure ranges, making them particularly effective in applications where precision is crucial. This section outlines the different types of manometers, namely simple manometers and differential manometers, and explains the calculations involved in determining pressures using these instruments.
The discussion encompasses the pressure equations derived from hydrostatic principles, illustrating the concept of pressure equilibrium across horizontal planes, and how this can be applied to both inclined and U-tube manometers. Important examples include the calculation of pressure using manometers of different configurations, emphasizing the setup involving varying liquid densities, which is vital in practical engineering applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Manometers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us come to the manometer. Very simple devices are used to measure the pressure like you have a, let have these type of conduit, the pipes the carrying any liquids and you want to measure it what could be the pressure on that pipe. So we can just insert the tubes like you can see can have the tube like this or can have a tube like this with inclined and all or you can have a inclined like this.
Detailed Explanation
Manometers are simple devices consisting of tubes used to measure the pressure within conduits or pipes carrying liquids. The setup allows us to see how different configurations, such as vertical or inclined tubes, affect the measurement of pressure. By inserting these tubes into the fluid system, we can allow liquid to rise or fall, indicating the pressure levels.
Examples & Analogies
Think of a manometer as a simple measuring stick for pressure, much like a ruler that measures the height of water in a glass. Just as the height tells you how much water is in the glass, the height of liquid in the manometer tells you the pressure in the pipe.
Basic Working Principle
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Each one having the merit and also disadvantage, like for examples, the manometer is simple device that is what use a liquid column to measure the pressure between two points okay. So in this case, we are measuring the pressures at for these the conduit the pipes using just a simple manometer or liquid columns to measure the pressure.
Detailed Explanation
The manometer operates on the principle of hydrostatics, where the height of the liquid column is related to the pressure exerted by the fluid. The manometer gives us a visual representation of the pressure difference between two points in a fluid system. Thus, if the liquid height increases or decreases in the manometer, it indicates changes in pressure.
Examples & Analogies
Imagine a balloon being filled with air. The more you inflate the balloon, the more tension is created inside. Similarly, the height of the liquid in the manometer changes with the pressure inside the pipe, serving as an indicator of how much 'inflation' or pressure is present.
Types of Manometers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
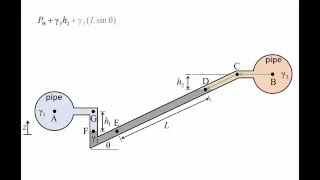
Similar way you can have a inclined one or just a vertical one or the having this concept of the half rectangular case. See if you look it that in case of the inclined one that if I have the inclined length is l that means the height of the liquid rest is h = l sin(θ) which is the projections of the incline.
Detailed Explanation
Manometers can take various shapes, such as vertical or inclined tubes. An inclined manometer is particularly useful for measuring low pressure, as it maximizes the vertical projection of liquid height due to the incline. The relationship between the incline, liquid height, and pressure is established through trigonometric functions like sine, which helps compute the actual pressure easily.
Examples & Analogies
Consider pouring water into a slanted cup versus a straight cup. In the slanted cup, the same volume of water appears higher than in the straight cup due to the angle. This analogy illustrates how inclined manometers amplify the visible height change for better pressure readings.
Using U-Tube Manometers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But sometimes we use the U tube manometers. That means we do not insert just a column. We make a U-shaped manometer; we make it U shape. And we also put different fluid on this. So like for example we will have different liquids like a heavier or the lighter.
Detailed Explanation
U-tube manometers consist of a U-shaped tube filled with a liquid that can show pressure differences between two points in a fluid system. The difference in liquid heights in the two arms of the U-tube indicates the pressure difference. The liquid used can vary, allowing for adaptability depending on the working fluids being measured.
Examples & Analogies
Imagine a seesaw with children on either side. If one child is heavier, that side of the seesaw goes down while the other goes up. In a U-tube manometer, the heavier liquid will cause a difference in height between the two arms, visually representing the pressure difference.
Pressure Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
See if you look it that in case of the inclined one that if I have the inclined length is l that means the height of the liquid rest is h = l sin(θ). But sometimes we use the U tube manometers. That means we do not insert just a column. We make a U-shaped manometer.
Detailed Explanation
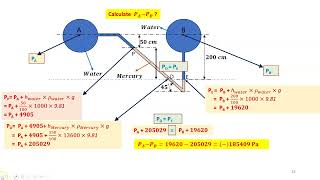
The height difference in the liquid columns can be used in calculations to find out the pressures at various points. With given liquid densities and height measurements, we can derive equations that give us the pressure at point A referenced from point B. Using basic hydrostatic equations, we can determine the effective pressures in the system.
Examples & Analogies
Think of using a scale to weigh two different fruits. Just as you take a reading to determine how much heavier one is than another, in pressure calculations, we determine how much more pressure exists at one point compared to another by utilizing the heights in our manometer.
Advantages of Inclined Manometers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Another case let we have an inclined manometer which is have a quite advantage in the sense that it amplifies the pressure reading as compared when you talking about low pressure ranges.
Detailed Explanation
Inclined manometers are particularly advantageous for measuring low-pressure readings as the incline increases the liquid column length corresponding to the same pressure difference compared to a vertical manometer. This larger height translates to more pronounced and easier-to-read results.
Examples & Analogies
Consider squeezing a sponge. If you squeeze lightly, hardly any water comes out; but if you squeeze more, a great burst of water is released. In a similar vein, inclined manometers make small changes in pressure more observable, akin to a gentle squeeze resulting in visible water flow rather than a flat and hard-to-see drip.
Differential Manometers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now there is another type of manometer which is called the differential manometers. As the name says that here, we do not measure a particular point pressure measurements where you consider two points.
Detailed Explanation
Differential manometers are designed to measure the difference in pressure between two points rather than measuring the absolute pressure at a single point. This makes them useful for applications where the pressure difference is critical, such as in pipe flow systems or systems where fluid movement is driven by pressure differences.
Examples & Analogies
Think of differential manometers like a race between two runners. Instead of measuring how fast each one runs independently, you are only interested in who is ahead and by how much. In fluid systems, what matters is how much pressure pushes fluid through a pipe, not what the single pressures are at given points.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Inclined Manometer: A manometer that has an angle of inclination to measure low pressure changes more effectively.
-
Differential Manometer: A tool to measure the difference in pressure between two points in a pipe or fluid system.
-
Hydrostatic Principle: The principle that allows for pressure measurement based on the height of a fluid column.
-
Pressure Calculation: The practice of determining pressure using the equation P = ρgh, where ρ is fluid density.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Calculate the pressure in a pipe using an inclined manometer where the liquid column height is measured at 20 cm and the angle of inclination is 30 degrees.
-
Example 2: Using a differential manometer to measure pressure difference across points A and B in a fluid system, where the heights of the columns are known.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
If the pressure lies beneath, in liquid's height you'll see,
A manometer will point it out, just trust the liquid's decree.
📖 Fascinating Stories
-
Once upon a time, in a laboratory, a curious engineer wanted to find out the pressure in a mysterious pipe. With an inclined manometer, they discovered that the angle could amplify their reading, revealing secrets hidden in the pressure — a true engineering adventure!
🧠 Other Memory Gems
-
Use 'MAD' to remember: M for Measurement, A for Angle, D for Difference — essential for understanding manometers!
🎯 Super Acronyms
Remember 'HAP' for Hydrostatic, At rest, Pressure when considering fluid pressure at rest.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Manometer
Definition:
A device used to measure the pressure of a liquid by balancing it against a column of another liquid.
-
Term: Hydrostatic Pressure
Definition:
Pressure exerted by a fluid at rest due to the weight of the fluid directly above.
-
Term: Inclination
Definition:
The angle at which the manometer is set compared to the horizontal, enhancing its sensitivity.
-
Term: Differential Manometer
Definition:
A manometer designed to measure the pressure difference between two points in a fluid.
-
Term: UTube Manometer
Definition:
A type of manometer consisting of a U-shaped tube filled with liquid, used to measure pressure differences.