Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Stress Tensors
Unlock Audio Lesson
Today, we’ll explore the components of the stress tensor, a crucial concept in both fluid and solid mechanics. Stress is defined as force per unit area. Can anyone tell me how many components are involved in a stress tensor?
Are there nine components in total?
Exactly! There are nine components that represent different forces acting on a tetrahedral structure. These include both normal stresses and shear stresses.
What are the differences between normal and shear stresses?
Great question! Normal stresses act perpendicular to a surface, while shear stresses act parallel to it. This distinction is important for analyzing fluid behavior.
Understanding Normal and Shear Stresses
Unlock Audio Lesson
Let’s break down the normal and shear stress components. Who can remind me what we understand by normal stress?
Normal stress is related to pressure and viscous stresses.
Correct! The diagonal components of the stress tensor correspond to these normal stresses. Now, what about shear stress?
Shear stress is only due to the viscous forces acting on the fluid.
Exactly! Understanding these stresses helps us analyze how fluids exert forces on surfaces.
Calculating Forces Using Stress Tensors
Unlock Audio Lesson
Now that we have a grasp of stress components, let’s look at how to calculate total forces on a control volume. Can anyone describe how we find the total force?
Is it through integrating stress over the surfaces?
That's right! We perform surface integrals to compute surface forces and volume integrals for body forces. This approach is fundamental to applying the Reynolds transport theorem.
So, we look at both the body force, like gravitational force, and surface forces, right?
Precisely! Recognizing both types of forces is critical for accurate fluid analysis.
Application of Stress Tensors
Unlock Audio Lesson
Let’s reflect on the significance of stress tensors in real-world applications. Why do we need to ensure that we account for both normal and shear stresses in engineering problems?
If we ignore shear stresses, we might miscalculate how a fluid interacts with surfaces.
Exactly! Properly calculating these interactions is vital for successful engineering designs. We have to account for the various stress components to ensure safety.
Can you illustrate this with an example of a structure?
Consider a dam, which withstands both hydrostatic pressure and shear forces from water currents. Understanding stress tensor components is essential in its design and safety assessment.
Concluding Thoughts on Stress Tensors
Unlock Audio Lesson
To conclude, can anyone summarize the key points regarding stress tensors we discussed today?
We learned about the nine components, how to calculate forces, and the significance of normal and shear stresses.
Also, how these concepts apply to real-world engineering scenarios!
Well done, everyone! Understanding these principles helps us tackle complex fluid mechanics problems. Keep reflecting on how these concepts interconnect as we proceed.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section details the nine components of the stress tensor, explaining how they are derived from surface forces acting on tetrahedral structures. It discusses the differences between normal and shear stresses, and illustrates how these components interact through various integrations to analyze fluid dynamics effectively.
Detailed
Detailed Summary
The concept of stress in fluid mechanics is fundamental, and it closely mirrors that in solid mechanics. Stress is defined as the force per unit area acting on a surface, which can be described by a stress tensor. In fluid dynamics, this stress tensor consists of nine components, arising from the three-dimensional nature of forces acting on a tetrahedral element with dx, dy, and dz components.
The diagonal components of the stress tensor correspond to normal stresses, which include contributions from pressure and viscous forces; while the off-diagonal components represent shear stresses, related purely to viscous forces. The section emphasizes that analyzing these components is crucial for solving problems involving surface forces and stresses in fluid flows.
Additionally, the discussion touches upon calculating total forces acting on control volumes, including surface and body forces. It explains how integrating stress components over control surfaces and volume integrals helps in determining resultant forces. Understanding this framework provides a foundation for applying methods such as Reynolds transport theorem and momentum equations in practical settings.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Stress Tensor
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
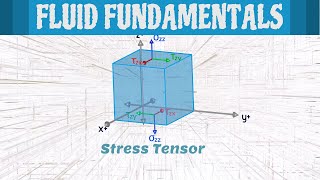
Now, if you come back to the surface forces, like for example, for tetrahedral structures like this where you have dx, dy, and dz components are there, and your axis is like this, x direction, y direction, and z direction. So, you can define the surface forces as a stress tensor. Stress means what, force per unit area. So, you can define as a stress tensor. So, this stress will have nine components. You could have this knowledge in solid mechanics.
Detailed Explanation
A stress tensor is a mathematical construct used to describe the internal forces within a material or fluid. It comprises components representing forces acting in all three spatial directions (x, y, z). Since a stress tensor accounts for forces acting on different planes, it consists of 9 components: three normal stress components (acting perpendicularly to the surface) and six shear stress components (acting parallel to the surface). The concept of stress as a force per unit area is similar to both solid and fluid mechanics.
Examples & Analogies
Imagine a sponge (representing a fluid) being squeezed. The force you apply on the sponge (pressure) generates stresses throughout its volume. The normal stress acts on the surface of the sponge where you apply pressure, while shear stress describes how the layers of the sponge slide past each other as you apply force.
Understanding Stress Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, you have the stress tensor coordinate systems defining nine stress components. If you look at that, if you take this diagonal component which is the normal component to this surface like, these are all normal components. That means these are compositions of the pressure force and the viscous force component. But the diagonal component what we have is acting tangentially. So, basically these are the viscous terms.
Detailed Explanation
The nine components of the stress tensor reflect the interactions between normal and shear forces at any point within a material. The diagonal components of the stress tensor correspond to normal stresses (acting perpendicular to specific surfaces), while the off-diagonal components account for shear stresses (acting parallel to these surfaces). In fluids, normal stresses include contributions from pressure, while viscous stresses arise from the internal friction in the fluid, which resists flow.
Examples & Analogies
Consider a layer of honey (viscous fluid) spread between two plates. As one plate moves, it exerts shear stress on the honey, while the pressure from the weight of the honey above creates normal stress. The way these stresses interact affects how the honey flows between the plates.
Surface Forces and Integrals
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, we can solve the problems considering the surface force defined as stress tensors and defining as normal stress and the shear stress component. The normal stress is a composition of pressure and viscous stresses, whereas shear stresses is only the viscous stress that we get.
Detailed Explanation
When analyzing fluid flow, it’s crucial to decompose surface forces into normal and shear stresses to understand how they affect the motion of the fluid. Normal stresses affect how fluids push against boundaries, while shear stresses influence how fluids slide over one another. We can calculate these forces mathematically using integrals over surfaces to account for the entire distribution of stresses acting on control volumes.
Examples & Analogies
Think about a river flowing over rocks. The water exerts pressure on the rocks, creating normal stress, while the flowing water can cause the layers of water to slide past each other, generating shear stress. Understanding these stresses is essential for designing bridges and dams.
Mathematical Representation of Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, if I have the stress component there and I have the normal vectors, if I resolve the force components, I will have the scalar product between the stress tensor and the n vectors, that is how we do it. And for the total surface area, we do surface integrals to compute it.
Detailed Explanation
The mathematical modeling of stresses involves using vector calculus to compute forces. By taking the dot product of the stress tensor with normal vectors, we can find out the effective force exerted on small surface areas. These force calculations are crucial for understanding how different parts of a fluid interact with surfaces, and we often use integrals to sum such forces over entire surfaces in a system.
Examples & Analogies
Imagine trying to calculate how much water pressure is acting against a dam wall. By integrating the pressure (stress) applied by the water along the dam surface (normal vectors), engineers can determine the total force exerted, which is essential for dam design.
Total Force Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The total force acting on the control volume will have the body force component and surface force component.
Detailed Explanation
In fluid dynamics, forces can be categorized into body forces (like gravitational forces acting throughout the fluid volume) and surface forces (like pressure forces acting on the surface boundaries). To effectively solve fluid dynamics problems, one must consider both types of forces when balancing equations related to motion and stress.
Examples & Analogies
Consider a balloon filled with water. The weight of the water inside creates a body force (gravity), while the pressure exerted on the walls of the balloon represents the surface force. Understanding both forces is vital when predicting how the balloon behaves when squeezed.
Simplifying Pressure Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When you apply the linear momentum equations to a control volume, like I have the control surface...we consider the atmospheric pressure is acting throughout this control surface...
Detailed Explanation
When analyzing forces acting on a control volume in fluid dynamics, atmospheric pressure is often considered to be uniform on the control surface. However, during integrative calculations, this atmospheric pressure effectively cancels out, leading us to focus on gauge pressure, which is the pressure above atmospheric pressure. This simplification allows for more straightforward calculations regarding fluid motion and forces.
Examples & Analogies
Think about measuring tire pressure. We rarely care about the atmospheric pressure acting on the tire's surface; instead, we're interested in the gauge pressure—how much pressure is inside the tire above the atmospheric level—which is crucial for understanding its performance.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Stress Tensor: A representation of internal forces within a material, showing how they vary across different dimensions.
-
Normal Stress: Component of stress acting perpendicular to the surface.
-
Shear Stress: Component of stress acting parallel to the surface, influenced by viscosity.
-
Surface Forces: Forces exerted on a surface area, critical for analyzing fluid behavior.
-
Body Forces: Forces that act throughout the material volume, such as gravity.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When considering a fluid flowing over a surface, the stress tensor helps predict how the fluid will exert pressure and tangential forces on the surface.
-
In a dam structure, engineers leverage the stress tensor to analyze the forces acting on the structure to ensure safety against water pressure.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Stress tensor, just remember, nine components in a blender. Normal and shear, they help steer, how fluids apply forces near.
📖 Fascinating Stories
-
Imagine a fluid like a dancer on a stage. The dancers' movements represent shear stress, while how they push against the walls symbolizes normal stress. Together, they create a dynamic performance of fluid mechanics.
🧠 Other Memory Gems
-
To remember stress components, use the acronym 'NSS' for Normal, Shear, and Surface forces.
🎯 Super Acronyms
For remembering the types of stress, use the acronym 'NSB' for Normal Stress, Shear Stress, and Body Force.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Stress Tensor
Definition:
A mathematical construct that describes the internal forces acting within a material, defined by its components corresponding to different force directions.
-
Term: Normal Stress
Definition:
Stress that acts perpendicular to the surface, including pressure and viscous components.
-
Term: Shear Stress
Definition:
Stress that acts parallel to the surface, resulting purely from viscous forces.
-
Term: Surface Force
Definition:
The force per unit area applied on a surface by a fluid or solid.
-
Term: Body Force
Definition:
A force that acts throughout the volume of a material, such as gravitational force.