Reynolds Transport Theorem
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Stress Tensors
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome, everyone! Today, we're focusing on the Reynolds Transport Theorem. Let's start with stress tensors. Can anyone tell me what a stress tensor represents in fluid mechanics?

Isn't it a way to describe forces acting within a fluid?

Exactly! It represents internal forces. Now, a stress tensor has nine components. Who can name these?

Normal and shear components?

Right! The normal components relate to pressure, while shear components are linked to viscosity. Remember, N for Normal and S for Shear—like 'N' in Pressure Normal!

So, what about those nine components? How do we get them?

Great question! They’re derived from our coordinate system, with each influence coming into play. Whether you consider x, y, z directions, it all rolls into the tensor structure. Now, who can summarize what the normal stresses correspond to?

They’re linked to both pressure and viscous stresses, right?

Exactly! And this understanding is crucial as we move to integrate these concepts into control volume analysis.
Control Volume Concepts
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we understand stress tensors, let's discuss control volumes. What is the significance of choosing a control volume?

It helps us visualize and calculate the forces acting on fluids?

Absolutely! Perfect selection allows us to manage variables effectively. Can someone explain how body and surface forces play into this?

Body forces are like gravity acting on the fluid volume, whereas surface forces arise from pressure on the boundaries.

Right! Don't forget that surface forces come from our stress tensor integrals as well. We integrate over the control surface to get total forces. Think of both forces as forming a comprehensive force balance!

So if we know both surface and body forces, we can calculate the overall momentum changes?

Exactly, well done! Understanding these balances is critical in applying the RTT in practical problems.
Equations and Integrals
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s delve into the actual equations of RTT. Who can recap what this theorem connects?

It connects the change in momentum of a control volume to net forces acting on it.

Perfect! So how do we express this mathematically?

Do we use surface and volume integrals to compute forces?

Correct! Volume integrals represent body forces while surface integrals represent the effects from pressure and shear. Can anyone give a simple form of this relationship?

Force equals mass times acceleration, right?

Exactly! That's the foundation from solid mechanics we apply here. This connection helps apply to various scenarios in fluid systems.
Practical Applications
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s examine how RTT is applied in engineering. What kind of problems can benefit from understanding this theorem?

Maybe problems related to fluid flow in pipes?

Exactly! That's a prime example. By applying RTT, we can predict pressure losses or flow rates. How about applications in open channels?

We can analyze flow rates when water discharges into the atmosphere.

Great insight! The gauge pressures and neglecting atmospheric pressure during discharges simplify calculations. Can anyone summarize the key takeaway for applying RTT?

Choose the right control volume and understand your forces at play!

Well said! Those principles will guide effective problem-solving in fluid engineering scenarios.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section discusses the fundamentals of the Reynolds Transport Theorem (RTT) in the context of fluid mechanics, explaining the concepts of stress tensors, body and surface forces, and their integration over control volumes to analyze fluid behavior and momentum changes. Key equations are presented alongside their significance in solving engineering problems.
Detailed
Reynolds Transport Theorem
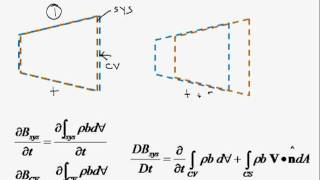
The Reynolds Transport Theorem (RTT) serves as a fundamental principle in fluid mechanics that provides a connection between the behavior of fluid particles and the flow of fluid through control volumes. At the heart of this theorem is the influence of surface forces, specifically described through stress tensors. Each stress tensor consists of nine components that account for various force interactions between fluid particles.
Key Concepts
- Stress Tensor: A mathematical representation capturing the distribution of internal forces within a fluid. In fluid mechanics, the stress often separates into normal components (related to pressure) and shear components (related to viscosity).
- Surface and Body Forces: The total forces acting on a control volume can be divided into body forces (such as gravity) and surface forces (resulting from pressure and viscous effects). Evaluating these forces involves integrating over the control surface and volume, respectively.
- Control Volume Analysis: By defining appropriate control volumes, engineers can simplify complex fluid behaviors into manageable mathematical forms, allowing for the computation of the net force acting on the fluid system.
Importance of RTT
The RTT not only underpins the mathematical modeling of momentum in fluid systems but also enables engineers to derive practical solutions to challenges in civil and mechanical engineering applications. For instance, in flow through pipes or impacts of jets, applying RTT allows for deriving effective force balance equations that inform design decisions.
Youtube Videos

![Get to know Reynolds Transport Theorem - part I [Fluid Mechanics]](https://img.youtube.com/vi/BwOnHIsgK_Q/mqdefault.jpg)





Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding the Stress Tensor
Chapter 1 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now, if you come back to the surface forces, like for example, for tetrahedral structures like this where you have dx, dy, and dz components are there, and your axis is like this, x direction, y direction, and z direction. So, you can define the surface forces as a stress tensor. Stress means what, force per unit area. So, you can define as a stress tensor. So, this stress will have nine components.
Detailed Explanation
The concept of stress in mechanics is crucial for understanding forces acting on objects. A stress tensor is a mathematical construct that represents the internal forces (stresses) within a material. It quantifies how these forces are distributed across different surfaces within the object. The stress tensor has nine components in three-dimensional space, which correspond to the forces acting in different directions: two for normal forces (perpendicular to a surface) and the others for shear forces (parallel to a surface).
Examples & Analogies
Think of a sponge under pressure, like when you squeeze it with your hand. The pressure applied creates stresses inside the sponge, pushing against different internal surfaces. Just like the stress tensor captures how the internal forces are distributed inside the sponge, it helps us understand how forces act within materials under various conditions.
Components of the Stress Tensor
Chapter 2 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, you have the stress tensor coordinate systems defining nine stress components. If you look at that, if you take this diagonal component which is the normal component to this surface like σ₁, σ₂, these are all normal components. That means these are compositions of the pressure force and the viscous force component. But the diagonal component what we have is σ₃, σ₄, and all, which is acting tangentially.
Detailed Explanation
The nine components of the stress tensor can be categorized into two main types: normal stresses, which act perpendicular to the surfaces, and shear stresses, which act parallel to the surfaces. Normal stresses are related to how much pressure the material is under, while shear stresses arise from the viscosity of the material, representing how it resists flow. These components help define how the material will behave when forces are applied.
Examples & Analogies
Imagine a set of books stacked on a shelf. The weight of the books pressing down creates a normal stress on the shelf. If someone pulls a book sideways, that creates shear stress on the books and the shelf. Understanding both types of stress helps us design stronger shelves that can hold more weight without bending or breaking.
Calculating Surface Forces
Chapter 3 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
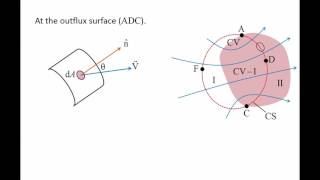
Now, if I have the stress component there and I have the normal vectors, if I resolve the force components, I will have the scalar product between the stress tensor and the n vectors, that is how we do it. And for the total surface area we do surface integrals to compute it.
Detailed Explanation
To determine the total forces acting on a surface, we use the concept of surface integrals, where we calculate the forces on each infinitesimally small piece of the surface. By taking the scalar product of the stress tensor and the normal vector to the surface, we can find out how much force acts in each direction and then sum it up across the entire surface area.
Examples & Analogies
Consider a flat, thin pizza. To find out how much weight the pizza dough can bear before it collapses, you'd evaluate how much pressure is applied by various toppings across every slice of pizza. By aggregating the forces from each topping on the dough, you can determine the total pressure experienced by different areas.
Body Forces and Surface Forces
Chapter 4 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The total force acting on the control volume will have the body force component and surface force component. The body force component will have volume integrals of rho g dV, g is the vector quantity as we consider the g, acceleration due to gravity.
Detailed Explanation
Forces acting on a control volume can be divided into body forces and surface forces. Body forces, like gravity, act throughout the material (e.g., the weight of fluid in a tank), while surface forces act at the boundaries (e.g., pressure forces on the walls of a tank). By using volume integrals for body forces and surface integrals for surface forces, we can compute the total forces on a volume.
Examples & Analogies
Imagine a water balloon. The gravity pulling down on the water (body force) affects every drop inside, while the pressure exerted on the surface of the balloon (surface force) affects only the material of the balloon itself. Understanding both types of forces helps engineers design stronger and safer containers for liquids.
Simplifying Linear Momentum Equations
Chapter 5 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now, if I divide the force components, that means, the total force will be one component from this body force, it is gravity force component. The surface force component we can resolve it into the force due to the pressure, force due to viscosity.
Detailed Explanation
When applying the linear momentum equations, we can simplify the total force by splitting it into its components: the gravitational body force and the various surface forces due to pressure and viscosity. This separation allows for a clearer analysis of each force's contribution to the overall behavior of the system, making it easier to apply principles of fluid mechanics.
Examples & Analogies
Think of a car driving down a slope. The weight of the car (gravity) pulls it down the slope (body force), while the friction between the tires and the road (surface force) resists that motion. By understanding both forces, we can predict how fast the car will go and how much stopping power it will need on the way down.
Atmospheric Pressure Neutralization
Chapter 6 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If you can understand it, if I take a control volume, everywhere I will have atmospheric pressure, then the absolute pressure from some locations. So, if I consider the atmospheric pressure is acting throughout this control surface and do surface integral, if the pressure is having the direction, and if I do a surface integrals over this, it will be cancelled out and becomes 0.
Detailed Explanation
In many engineering applications, the effects of atmospheric pressure can be neglected when analyzing forces within a control volume. Since atmospheric pressure acts equally in all directions and integrates out to zero in enclosed spaces, we can focus on gauge pressures instead, which simplifies calculations while still capturing the essential physics of the problem.
Examples & Analogies
Imagine a sealed balloon at sea level. The pressure inside the balloon is influenced by atmospheric pressure, but when calculating how much the balloon expands or contracts, the atmospheric pressure can be ignored since it affects all parts equally. Instead, we can focus solely on the additional pressure generated by the air inside the balloon.
Key Concepts
-
Stress Tensor: A mathematical representation capturing the distribution of internal forces within a fluid. In fluid mechanics, the stress often separates into normal components (related to pressure) and shear components (related to viscosity).
-
Surface and Body Forces: The total forces acting on a control volume can be divided into body forces (such as gravity) and surface forces (resulting from pressure and viscous effects). Evaluating these forces involves integrating over the control surface and volume, respectively.
-
Control Volume Analysis: By defining appropriate control volumes, engineers can simplify complex fluid behaviors into manageable mathematical forms, allowing for the computation of the net force acting on the fluid system.
-
Importance of RTT
-
The RTT not only underpins the mathematical modeling of momentum in fluid systems but also enables engineers to derive practical solutions to challenges in civil and mechanical engineering applications. For instance, in flow through pipes or impacts of jets, applying RTT allows for deriving effective force balance equations that inform design decisions.
Examples & Applications
In a pipe subjected to internal fluid flow, the stress tensor helps understand how pressure and viscous forces distribute along the fluid.
When analyzing discharge from a water jet, RTT enables predictions on force exerted on structures due to the jet impact.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In a fluid so slick, with forces so quick; Stress tensors at play, control volumes sway.
Stories
Imagine a river flowing through various landscapes. The bends and the banks of the river represent control volumes. Within those banks, stress tensors depict the pressures and forces at play, shaping the flow and the landscape.
Memory Tools
Forces in Fluid: F - Forces (Body, Surface), S - Stress (Tensors), C - Control Volume (Analyze), I - Integrals (Calculate). Remember: 'FSC-I.'
Acronyms
Remember 'BSC' for Body forces, Surface forces, and Control volumes in fluid dynamics.
Flash Cards
Glossary
- Stress Tensor
A mathematical representation that describes the state of stress at a point in a fluid, encompassing both normal and shear stress components.
- Control Volume
A predefined volume in space through which fluid flows, used to analyze fluid behavior and quantify forces acting on it.
- Body Force
A force acting on a fluid body due to a field, such as gravity, which influences the entire volume of fluid.
- Surface Force
Forces acting on the surfaces of a fluid body due to pressure and shear stress.
- Integrals
Mathematical operations that calculate the total accumulation of quantities over a specified range, applied here for analyzing forces.
Reference links
Supplementary resources to enhance your learning experience.
