Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Stress Tensors
Unlock Audio Lesson
Today, we're diving into stress tensors, which represent the internal forces in a fluid. What do you think stress refers to in this context?
I think it might relate to how much force is exerted over an area, right?
Exactly! Stress is defined as force per unit area. In fluids, we describe these stresses with a tensor that has nine components.
Can you explain why there are nine components?
Sure! Each component corresponds to a combination of normal and shear stresses, acting along different surfaces. The three dimensions - x, y, and z - contribute to this complexity.
I see! So, normal stresses act perpendicular to surfaces while shear stresses are tangent?
Exactly right! Remember: NTS for Normal and Tangential Stresses. Now, let’s move to how we use these in control volumes.
Application of Control Volumes
Unlock Audio Lesson
Let's discuss control volumes. Why do you think defining one correctly is essential in fluid mechanics?
Because it helps analyze the forces acting on that specific volume of fluid?
Yes, and you want to include both body forces and surface forces. Can anyone describe how we mathematically compute these?
I remember something about using integrals to sum forces over the surface area!
Correct! It involves surface integrals for external forces and volume integrals for internal forces. Great job!
What happens with atmospheric pressure in these calculations?
Good question! The contributions from atmospheric pressure cancel out, allowing us to work with gauge pressure. Think of it as balancing forces— it simplifies our calculations.
Linear Momentum Equations
Unlock Audio Lesson
Now, let’s shift our focus to linear momentum equations using Reynolds Transport Theorem. Why is momentum important in fluid systems?
Momentum helps in understanding how forces affect fluid flow!
Exactly! Remember, linear momentum relates to mass and acceleration. Can anyone provide me with the equation form for this?
Isn’t it F = m*a?
That's right! Now, for a control volume, we represent momentum flux as the net force acting on it. We combine surface and volume integrals accordingly.
Practical Applications of Momentum Flux
Unlock Audio Lesson
Let’s explore momentum flux in practical scenarios. How would we calculate it if we have multiple inlets and outlets in our control volume?
We would analyze the momentum coming in and going out, right?
Yes! We compute mass fluxes across all inlets and outlets to find the net momentum flux. What implications does this have?
I think it helps ensure we’re balanced in our force applications, correct?
Absolutely! Remember: 'Momentum in equals Momentum out.' This principle is fundamental in fluid mechanics.
Reynolds Transport Theorem (RTT)
Unlock Audio Lesson
To wrap up our discussions, let's look at the Reynolds Transport Theorem. Why could it be beneficial?
It helps connect system and control volume analyses!
Exactly! It provides a bridge between the two. We can use it to derive equations related to momentum flux in fluid flows.
Can it also simplify calculations?
Yes, particularly when we apply it to fixed control volumes. In steady-state conditions, we can also ignore certain components.
This wraps everything together neatly!
That's the idea! Remember, mastering this theorem will help you solve complex fluid mechanics problems more efficiently.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section highlights the importance of stress tensors in describing surface forces in fluid mechanics. It elaborates on how to apply linear momentum equations to control volumes, taking into account body forces, surface forces, and pressure distribution while recognizing the role of atmospheric pressure.
Detailed
In fluid mechanics, the analysis of surface forces is crucial, and this section emphasizes how stress tensors can articulate these forces through their nine components in Cartesian coordinates. The concepts of normal and shear stresses are defined, accounting for pressure and viscous forces. Students learn how to resolve forces acting on control volumes, including surface and body forces through integrals. The atmospheric pressure's cancellation is discussed when considering control volumes, guiding students to focus on gauge pressure for practical applications. Moreover, control volume selection, linear momentum equations, and the Reynolds transport theorem are vital in determining momentum flux relative to net forces acting on the control volume.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Stress Tensors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, if you come back to the surface forces, like for example, for tetrahedral structures like this where you have dx, dy, and dz components are there, and your axis is like this, x direction, y direction, and z direction. So, you can define the surface forces as a stress tensor. Stress means what, force per unit area. So, you can define as a stress tensor. So, this stress will have nine components.
Detailed Explanation
Stress is essentially the amount of force applied on a surface per unit area. When considering three-dimensional objects (like tetrahedra), we have forces acting on surfaces in three dimensions (x, y, z). The stress tensor captures this by describing how these forces (surface forces) are distributed across these dimensions with nine components altogether. Each component of the tensor corresponds to how much force is exerted in a particular direction on a particular face of the object.
Examples & Analogies
Imagine a balloon filled with air. If you poke at it from different sides, you're applying forces on the surface of this balloon. The stress tensor would help quantify how these forces are distributed across the interior of the balloon, impacting how it deforms based on where you poke.
Normal vs Shear Stress Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at that, if you take this diagonal component which is the normal component to this surface... These are compositions of the pressure force and the viscous force component. But the diagonal component what we have is ... and all, which is acting tangentially. So, basically these are the viscous terms.
Detailed Explanation
Stress can be categorized into normal stress and shear stress. Normal stress is the stress component acting perpendicular to the surface, resulting from either pressure or viscous forces. Shear stress, on the other hand, arises from forces acting parallel to the surface and is linked to the fluid's viscosity. Understanding this distinction is crucial for analyzing how materials and fluids behave under external forces.
Examples & Analogies
Think of a deck of cards. If you push down on the cards, you're applying normal stress. However, if you slide your hand across the top of the deck, you're applying shear stress. The cards can slide easily over each other, which represents how fluids might behave under shear stress situations.
Calculating Forces Using Stress Tensors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, if I have the stress component there and I have the normal vectors, if I resolve the force components... to compute it, okay? Please do not be more worried about how we are having a scalar product of stress tensors and normal factors which will be coming to be again a second order vector components.
Detailed Explanation
To calculate the total forces acting on an object using stress tensors, we often utilize scalar products of the stress tensor and normal vectors representing the surfaces of the object. The process involves integrating these products over the surface to determine the total impact of all forces acting on the object. This will help in determining how the object's momentum changes under these forces.
Examples & Analogies
Consider a floor with different tiles. Each tile can be viewed as a surface, and the forces pushing down (weight of furniture, people, etc.) will affect how they interact with one another. Using the stress tensor to model these interactions lets you predict how much overall pressure is distributed across the entire floor.
Body Forces vs Surface Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Total force acting on the control volume will have the body force component and surface force component. The body force component will have volume integrals of rho g dV, ... but many of the times we make alignments in such a way that only this k direction or negative direction and k is in upward direction.
Detailed Explanation
Forces acting on an object or fluid can be categorized as body forces and surface forces. Body forces are those that act throughout the volume of the object (like gravitational force, denoted
Examples & Analogies
Think about a tree: the wind blowing against it represents surface forces, while the gravitational force pulling it downwards illustrates body forces. Both types of forces affect how the tree moves and bends in the environment.
The Importance of Control Volumes in Fluid Dynamics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When you apply a linear momentum equations to a control volume, like I have the control surface like this, if you look at this control surface, in these three phases we have the pressure is atmospheric pressure.....
Detailed Explanation
A control volume is a defined region in space used to analyze fluid flow and momentum equations. In analyzing forces, we often consider pressures acting at the boundaries or surfaces of this volume. By defining the control volume carefully, we can simplify calculations by neglecting uniform pressures (like atmospheric pressure) that cancel out when integrated around the volume's surface.
Examples & Analogies
Imagine a blender filled with fruit. The control volume is the blender itself, and as you blend, the forces (like pressure from the rotating blades) act on the fruit inside. If you only cared about the fruit moving around in the blender and not outside forces (like air pressure), you can view the fruit’s behavior more simply.
Momentum Equations and Net Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
At this systems level force is equal to mass into acceleration... So, this is the basic equation which is linear momentum equation in Reynolds transport theorem point of view.
Detailed Explanation
The fundamental principle of dynamics is that the total force acting on a system equals the rate of change of its momentum (mass times acceleration). In the context of fluid dynamics, this relationship allows us to derive the linear momentum equations using the Reynolds transport theorem, which helps examine how fluid properties change as they move through a control volume.
Examples & Analogies
Think of a car speeding up on a highway. The force from the engine accelerates the car. If more passengers (mass) get into the car, a greater force must be applied to maintain acceleration. This principle of balancing forces and changes in motion mirrors the equations derived from fluid momentum principles.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Control Volume: A defined region in fluid flow for analysis of forces and moments.
-
Stress Tensor: Describes internal stress within fluids using normal and shear components.
-
Momentum Flux: The rate of momentum transfer through a surface, critical for force balance.
-
Reynolds Transport Theorem: Links system dynamics to flow across control surfaces.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
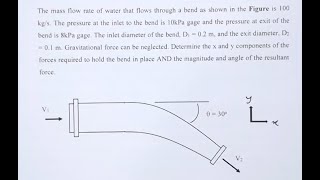
Calculating the stress tensor for a fluid in a pipe under various flow conditions.
-
Utilizing control volume concepts to analyze forces around a hydraulic structure.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In every fluid flow, forces do blend, stress and pressure, rules they'll send.
📖 Fascinating Stories
-
Imagine a fluid pastry, creamy and smooth. The stress tensor tells us how its layers groove.
🧠 Other Memory Gems
-
NTS = Normal is perpendicularly Tall, Shear is Tangent, standing small.
🎯 Super Acronyms
CVC = Control Volume Concept helps visualize flows.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Stress Tensor
Definition:
A mathematical representation that describes internal forces acting within a fluid by defining nine stress components.
-
Term: Control Volume
Definition:
A specified region within a fluid flow where the analysis of momentum, energy, and mass is conducted.
-
Term: Normal Stress
Definition:
Stress components acting perpendicular to a surface.
-
Term: Shear Stress
Definition:
Stress components acting tangentially to a surface.
-
Term: Reynolds Transport Theorem
Definition:
A principle yielding a relationship between the rate of change of quantity in a system and the flow of that quantity across a control surface.