Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Stress Tensor
Unlock Audio Lesson
Today, we are discussing the stress tensor, a concept crucial in both fluid and solid mechanics. Can anyone tell me what they think the term 'stress' refers to in this context?
Isn't it related to force acting on an area?
Correct! Stress is indeed force per unit area. The stress tensor encapsulates this concept in a mathematical framework. It has nine components, representing all possible surface forces acting in different directions.
What do the components of the stress tensor represent?
Great question! The diagonal components represent normal stress, while the off-diagonal components relate to shear or viscous stress. This tensor helps us analyze how materials respond to external forces.
How does this connect to solid mechanics?
The connection is quite significant. Many principles applied in solid mechanics are analogous to those in fluid mechanics concerning stress. This allows us to apply similar methods across disciplines.
To summarize, the stress tensor is fundamental in mechanics, allowing us to quantitatively express how forces affect materials and fluids.
Components of the Stress Tensor
Unlock Audio Lesson
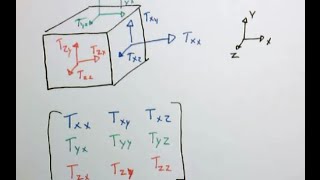
Let's dive deeper into the stress tensor's components. As mentioned earlier, there are nine components represented in a 3x3 matrix. Can someone remind me how these are arranged?
They are organized by their respective directions, right? Like xx, xy, xz, and so on.
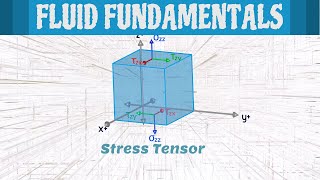
Exactly! The first index indicates the direction of the force, and the second index indicates the direction of the normal to the surface. For example, the component σ_xx refers to the stress in the x-direction acting on a surface whose normal is also in the x-direction.
What do the shear components mean?
The shear components, such as σ_xy, represent how the forces act parallel to the surface. They are crucial for analyzing material behavior under various loads.
Can we visualize this with a physical example?
Absolutely! Imagine a cube immersed in a fluid. The stresses applied on each face of the cube can be represented through these tensor components, helping us understand how the fluid exerts pressure and shear on the object.
In summary, these components provide a comprehensive view of stress within materials, essential for solving engineering problems.
Calculating Forces using the Stress Tensor
Unlock Audio Lesson
Now that we understand the components of the stress tensor, let's see how we can use it to calculate forces on a control volume. Who can tell me what a control volume is?
Isn’t it the space where we analyze forces acting in a fluid or solid?
Correct! We can apply surface integrals to compute the total forces acting on a control volume using the stress tensor and its components.
How do we set up these integrals?
We take the scalar product of the stress tensor with the differential area vectors, integrating over the surface of the control volume. This gives us the total surface force.
Is there a specific theorem we use to analyze momentum in fluids?
Yes, we're often guided by the Reynolds Transport Theorem in these analyses, which combines both the material and control volume approaches.
In conclusion, understanding the stress tensor allows for effective calculation of forces and analysis of behavior in engineering contexts.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The stress tensor is described as a critical tool for representing the various surface forces acting on a body, encompassing both normal and shear stresses. The section outlines its composition, which includes nine components reflecting forces in different directions and emphasizes the connection between solid mechanics and fluid mechanics in understanding stress.
Detailed
In this section, we explore the definition and implications of the stress tensor in both fluid and solid mechanics. The stress tensor is essential for describing surface forces acting on a differential element, characterized by its nine components representing different stresses (normal and shear) acting along various axes (x, y, z).The diagonal elements of the tensor relate to normal stresses, while off-diagonal elements (tangential components) correspond to shear stresses. Additionally, the relationship between the stress tensor and force components is elaborated upon, emphasizing the tensor's role in translating physical forces into mathematical representations through scalar products with normal vectors. This foundational understanding is vital for applying momentum equations and conducting surface integrals within a defined control volume in both disciplines.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Stress Tensor
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, if you come back to the surface forces, like for example, for tetrahedral structures like this where you have dx, dy, and dz components are there, and your axis is like this, x direction, y direction, and z direction. So, you can define the surface forces as a stress tensor. Stress means what, force per unit area. So, you can define as a stress tensor.
Detailed Explanation
A stress tensor is a mathematical representation that describes how forces are distributed over an area. When we talk about stress, we mean force applied to a specific area. In a three-dimensional space, we consider three axes: x, y, and z. Each axis can be divided into components, which ultimately form a tensor that characterizes the internal forces within a material.
Examples & Analogies
Think about a sponge being squished. The pressure you apply on the sponge can be thought of as the force per unit area. This pressure is distributed throughout the sponge, creating internal stresses. The stress tensor helps us understand how that pressure affects the sponge at different points.
Components of the Stress Tensor
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, this stress will have nine components. You could have this knowledge in solid mechanics. I am just repeating it. There is not much difference between solid mechanics and fluid mechanics when you consider at stress level.
Detailed Explanation
The stress tensor consists of nine components in three-dimensional space. These components represent normal and shear stresses acting in different directions. In both solid and fluid mechanics, the stress distribution is crucial for understanding how materials respond to applied forces. The normal stresses act perpendicular to the surface, while shear stresses act parallel to it.
Examples & Analogies
Imagine a block of cheese on a cutting board. If you push down on it (normal stress), the cheese squishes down, but if you slide your knife sideways across it (shear stress), the cheese deforms differently. The stress tensor captures all these actions in one complete picture.
Normal and Shear Stress Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, we have stress tensors in order to describe all surface force components. That is what will have nine components which will have, as you know the subscript describes that. The stress in the z direction acting on the face whose normal is eight directions. This is similar notation to what we use in solid mechanics.
Detailed Explanation
The nine components of stress in the tensor represent different types of stress experienced in a material. The diagonal components signify normal stresses (acting perpendicular to the surface), while the off-diagonal components denote shear stresses (acting parallel to the surface). This standardized notation helps engineers and scientists categorize and analyze stress conditions.
Examples & Analogies
Picture a multi-story building. Each floor has vertical supports that bear the weight of the floors above (normal stress) while also allowing for side-to-side movement during winds (shear stress). The stress tensor helps us analyze these forces to ensure the stability and safety of the building.
Evaluating Stress Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Over the surface we can define it, which is the shear stress components or the viscous stress component. So, these nine components of stress in Cartesian coordinates are defined in this surface. So, we can solve the problems considering the surface force defined as stress tensors and defining as normal stress and the shear stress component.
Detailed Explanation
In fluid mechanics, we also differentiate between shear stress components and viscous stress, which arises in fluid flow due to viscosity. To solve engineering problems, we rely on the surface forces defined by the stress tensor to account for both types of stress. This allows us to determine how materials will behave under various loading conditions.
Examples & Analogies
Think about oil flowing through a pipe. The viscous stress is what helps us understand how smoothly the oil flows, while the shear stress is what helps us manage the effects of the oil rubbing against the pipe's walls. Analyzing these stresses with a tensor gives us an accurate picture of the situation.
Application of Stress Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The normal stress is a composition of pressure and viscous stresses, whereas shear stresses is only the viscous stress that we get.
Detailed Explanation
Normal stress can be calculated by combining the effects of pressure from the fluid and the viscous stresses occurring due to the movement of fluid layers. In contrast, shear stress involves only the viscous components. This distinction is crucial in practical applications involving fluids, as it helps predict how they will exert forces on structures.
Examples & Analogies
Consider a water tank. When the tank is full, the weight of the water exerts pressure on the tank walls (normal stress). As the water flows out through a pipe, the friction between the flowing water and the pipe creates shear stress. Understanding these stresses is vital for designing safe tanks and piping systems.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Stress: A measure of internal forces distributed over an area.
-
Stress Tensor: Represents all surface forces acting on a solid or fluid in a comprehensive manner.
-
Normal Stress: Related to the internal forces acting perpendicular to a surface.
-
Shear Stress: Forces acting parallel to the surface, critical for understanding material deformation.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A cube submerged in water experiences both pressure (normal) stress from water and shear stress from fluid flow.
-
In a structural engineering context, a beam subjected to bending will experience normal stress on the top surface and shear stress at its neutral axis.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Stress all around, on surfaces abound, normal or sheer, forces all here!
📖 Fascinating Stories
-
Imagine a cube under water, feeling the pressure from every side, while the fluid flows around it, tugging at its edges; this defines how stress interacts.
🧠 Other Memory Gems
-
N&N: Normal & Newton. Remember, Normal stress is like the push or pull, while Newton shows how forces apply!
🎯 Super Acronyms
STRESS
- S- Surface
- T- Tension
- R- Rotation
- E- Equilibrium
- S- Shear
- S- Stiffness.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Stress Tensor
Definition:
A mathematical representation of surface forces acting on a body, characterized by its nine components, which include normal and shear stresses.
-
Term: Normal Stress
Definition:
The component of stress acting perpendicular to a surface, associated with compressive or tensile forces.
-
Term: Shear Stress
Definition:
The component of stress acting parallel to a surface, resulting from forces that cause deformation.
-
Term: Control Volume
Definition:
A defined space in which fluid flow is analyzed, allowing the application of conservation principles.