Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Magnetic Field Circulation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, weβre going to talk about Ampere's Circuital Law. Does anyone know how the magnetic field relates to electrical currents?
Isn't there a way to measure how much the magnetic field is generated by a current?
Exactly! Ampere's Law states that the integral of the magnetic field around any closed loop is proportional to the total current passing through that loop. We can express this mathematically as: $\oint B \cdot dl = \mu_0 I$.
What do the symbols mean?
Great question! $\oint B \cdot dl$ represents the line integral around the path, $\mu_0$ is the permeability of free space, and $I$ is the current that passes through the loop. It's an elegant way to connect magnetic fields to electrical currents.
Does that mean we can find the magnetic field's direction too?
Yes! The right-hand rule helps us determine the direction of the magnetic field induced by current. Remember, point your thumb in the direction of the current, and your fingers curl in the direction of the magnetic field lines.
To recap, Ampere's Law allows us to relate current and magnetic fields, demonstrating their intrinsic link in electromagnetism.
Application of Ampere's Circuital Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs consider how we can apply Ampere's Circuital Law in real situations. Can anyone give an example?
Can we use it to find the magnetic field of a straight wire?
Yes! For an infinitely long straight wire, Ampereβs Law simplifies to $B = \frac{\mu_0 I}{2\pi R}$, where $R$ is the distance from the center of the wire. This gives us a direct method to calculate the magnetic field created by a current-carrying wire.
And what about for a solenoid?
Good point, Student_2! For a long solenoid, the field inside is uniform and can be calculated using $B = \mu_0 n I$, where $n$ is the number of turns per unit length. This application is common in constructing electromagnets.
Is there a limit to where we can apply these formulas?
Ampere's Law holds best in symmetrical situations but can be more complex in irregular configurations. In such cases, we may need to revert to the Biot-Savart law.
To summarize, Ampereβs Circuital Law is a powerful tool in analyzing the magnetic effects of currents, especially in regular geometries like wires and solenoids.
Practical Calculations Using Ampere's Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's go over a practical example. Suppose we have a current of 5 A in a long straight wire. What would be the magnetic field at a distance of 10 cm from the wire?
Using $B = \frac{\mu_0 I}{2\pi R}$, I can substitute $I$ with 5 A and $R$ with 0.1 m, right?
Exactly, and whatβs the next step?
So I'd calculate $B = \frac{(4\pi \times 10^{-7}) \times 5}{2\pi \times 0.1}$. That simplifies to...
It calculates to 1.0 mT!
Great job! That is correct. Now, how about finding the field in the center of a tightly wound solenoid carrying the same current?
Using $B = \mu_0 n I$, we need to consider the number of turns per unit length.
Correct! Assume it has 100 turns per meter; what would the magnetic field be?
So $B = (4\pi \times 10^{-7}) \times 100 \times 5$, calculating gives me 6.28 mT.
Exactly! Keep practicing these calculations, as they reinforce how Ampere's Law can be utilized in various contexts.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Ampere's Circuital Law asserts that the integral of the magnetic field along a closed loop is proportional to the total current passing through the surface bounded by that loop. This law simplifies calculations for magnetic fields in cases of high symmetry and is central to understanding electromagnetism.
Detailed
Ampere's Circuital Law
Ampere's Circuital Law expresses a relationship between the magnetic field and the electrical current that produces it. The law can be summarized by the equation:
$$ B \cdot dl = \mu_0 I $$
where $B$ is the magnetic field, $dl$ is an infinitesimal segment of the closed loop, $\mu_0$ is the permeability of free space, and $I$ is the total current enclosed by the loop. The law highlights that the circulation of the magnetic field around a closed path is directly proportional to the current that passes through the surface enclosed by that path.
This section also discusses a simplified case acknowledging that for many symmetrical problems, one can derive the magnetic field with much more straightforward calculations using Ampere's law instead of Biot-Savart law. The discussion includes examples of using Ampereβs law for straight wires, solenoids, and enclosed currents.
In practice, Ampere's Circuital Law is crucial in electrical engineering and physics when calculating magnetic fields in symmetrical configurations, illustrating the intimate connection between electricity and magnetism.
Youtube Videos
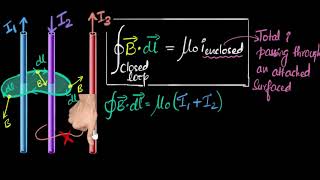
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Ampere's Circuital Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
There is an alternative and appealing way in which the Biot-Savart law may be expressed. Ampereβs circuital law considers an open surface with a boundary. The surface has current passing through it.
Detailed Explanation
Ampere's Circuital Law simplifies our understanding of magnetic fields created by electric currents. It considers a surface with a boundary (like a loop) where current flows through that surface. This law helps relate the magnetic field to the electric current effectively, providing a direct connection between current and the magnetic field generated around it.
Examples & Analogies
Think of a river (electric current) flowing and forming a boundary on a lake (the surface). The water level (magnetic field) along the boundary depends on how strong the river flows, similar to how the magnetic field strength is determined by the amount of current passing through the enclosed surface.
Mathematical Expression of Ampere's Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Ampereβs law states that this integral is equal to Β΅ times the total current passing through the surface, i.e., βB.dl = Β΅I, where I is the total current through the surface.
Detailed Explanation
The equation B.dl = Β΅I illustrates that when you take the integral of the magnetic field along a closed path, it is equal to the permeability (Β΅) multiplied by the total current (I) passing through the enclosed area. This reinforces how the magnetic field interacts with the current and emphasizes the magnetic influence of moving charges.
Examples & Analogies
Imagine walking along a circular track while carrying a baton. The path you walk (B.dl) signifies the magnetic influence, while the baton you hold represents the current (I). The more friends you have walking with you (higher I), the larger the influence on the track you create!
Special Cases and Simplifications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For several applications, a much simplified version of Ampereβs law proves sufficient. We shall assume that it is possible to choose the loop such that at each point of the loop, either (i) B is tangential to the loop and is a non-zero constant B, or (ii) B is normal to the loop, or (iii) B vanishes.
Detailed Explanation
In practical applications, we can often simplify the usage of Ampere's Law by assuming specific conditions regarding the arrangement of electric currents and the magnetic fields. This helps in straightforward calculations and ensures clarity in understanding the magnetic fieldβs properties in various common scenarios.
Examples & Analogies
Consider a bicycle wheel. If all spokes (the magnetic fields) point outward (are tangential) to the rim (the loop), moving around will feel uniform, just as uniform magnetic fields feel consistent when currents flow in predictable patterns. If the spokes donβt connect to the central hub (the loop), they disappear from influence, just like B may vanish in certain conditions.
Application of Ampere's Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When there is a system with symmetry such as for a straight infinite current-carrying wire, Ampereβs law enables an easy evaluation of the magnetic field.
Detailed Explanation
Utilizing symmetry in Ampere's Law can drastically simplify finding the magnetic field for certain setups, such as a long straight wire. By choosing a circular Amperian loop around the wire, we can easily calculate the magnetic field at a given distance using Ampereβs Law.
Examples & Analogies
Picture a straight rope (the wire) held taut in the center of a circular swimming pool (the Amperian loop). The water (magnetic field) flows uniformly around the rope, making it easy to determine how far the water will reach at any point. This analogy highlights how simple geometrical arrangements help in analyzing complex interactions.
Magnitude of the Magnetic Field due to a Long Straight Wire
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The boundary of the loop chosen is a circle and magnetic field is tangential to the circumference of the circle. The law gives the magnetic field at a distance r outside the wire as B = Β΅I/(2Οr).
Detailed Explanation
This formula indicates that the magnetic field (B) caused by a long straight current-carrying wire decreases in strength as we move further away from the wire. The immediate implication is that if we double the distance from the wire, we obtain a field half as strong, showcasing the inverse relationship with distance.
Examples & Analogies
Think of a flashlight beam. As you move away from the light source, the beam spreads out and the intensity diminishes. Similarly, the magnetic field from a wire spreads out, losing strength the further you are from it.
Right-Hand Rule for Magnetic Field Direction
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
There exists a simple rule to determine the direction of the magnetic field due to a long wire. This rule is called the right-hand rule: Grasp the wire in your right hand with your extended thumb pointing in the direction of the current. Your fingers will curl around in the direction of the magnetic field.
Detailed Explanation
The right-hand rule offers a simple way to visualize the direction of the magnetic field around a current-carrying wire. By curling your fingers around the wire in the direction of current flow, your thumb indicates the direction of the magnetic field lines, making it easy to determine their orientation.
Examples & Analogies
Envision holding onto a pipe (the wire) with your thumb pointing up (the current). As you grip the pipe, the direction your fingers naturally curl is similar to how the magnetic field wraps around it, helping to visualize this important connection in magnetism.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Ampere's Law: Relates the magnetic field in a loop to the current through it.
-
Magnetic Field (B): A field around electric currents.
-
Permeability of Free Space: A constant that measures the strength of magnetic fields.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
- For a straight wire carrying a current of 5 A, the magnetic field at a distance of 10 cm is approximately 1.0 mT.
-
- In a solenoid with 100 turns per meter and carrying 5 A, the magnetic field strength is 6.28 mT.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
In loops we find, currents lead, to magnetic fields that grow indeed.
π Fascinating Stories
-
Imagine a circuit party where every current is dancing around a magnetic loop; the more dancers, the stronger the music wavesβthis is how currents influence their magnetic field.
π§ Other Memory Gems
-
Remember: 'CIRCLES' - Current Induces Rotating Circular Loops of Electric Strongest magnetic fields.
π― Super Acronyms
BACON - 'B' for Magnetic field, 'A' for Ampereβs law, 'C' for Current, 'O' for the circle path, and 'N' for Loop.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Ampere's Circuital Law
Definition:
A law stating that the integral of the magnetic field around a closed loop is proportional to the total current passing through the surface bounded by the loop.
-
Term: Magnetic Field (B)
Definition:
A vector field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials.
-
Term: Permeability of Free Space (ΞΌβ)
Definition:
A physical constant that describes how magnetic fields interact with materials and is defined as ΞΌβ = 4Ο Γ 10^-7 TΒ·m/A.