Learn
Games

4.9.2 - Circular current loop as a magnetic dipole

Interactive Audio Lesson

Listen to a student-teacher conversation explaining the topic in a relatable way.

Understanding Magnetic Dipoles

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Today, we're discussing the concept of magnetic dipoles, particularly focusing on how a circular current loop can be considered a magnetic dipole. Can anyone remind me what a dipole is?

Student 1
Student 1

A dipole is a pair of equal and opposite charges or magnetic poles separated by distance.

Teacher
Teacher

Exactly! Now, how do you think a circular current loop behaves like a dipole?

Student 2
Student 2

Does it create a magnetic field similar to how electric dipoles create an electric field?

Teacher
Teacher

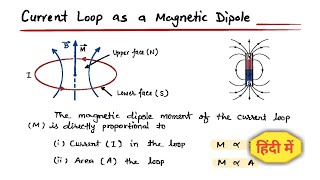
Great point! Let's explore that. The magnetic field produced by a current loop behaves similarly to the electric field of a dipole. The key is in the magnetic moment, denoted by **m**.

Student 3
Student 3

What is the formula for the magnetic moment of the loop?

Teacher
Teacher

Good question! The magnetic moment **m** is defined as **m = I × A**, where **I** is the current and **A** is the area of the loop. Can anyone calculate it for a loop with a radius of 2 cm and a current of 3 A?

Student 4
Student 4

The area would be π × (0.02 m)^2, which gives me approximately 0.00126 m².

Teacher
Teacher

Right! So what is the magnetic moment?

Student 1
Student 1

Multiplying 3 A by that area gives around 0.00378 A m².

Teacher
Teacher

Excellent! As we see, this magnetic dipole moment influences the magnetic field produced, similar to how charge influences an electric field.

Magnetic Field Around a Current Loop

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Now, let's delve into the specific formula for the magnetic field **B** produced by a circular current loop. What do you think is the formula for the magnetic field at a distance **x** along the axis?

Student 2
Student 2

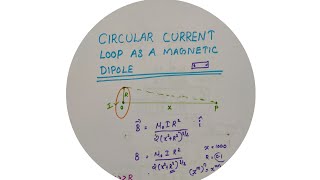
Isn't it supposed to be something like **B = \frac{µ_0 IR^2}{2(x^2 + R^2)^{3/2}}**?

Teacher
Teacher

Correct! As you can see, this equation takes into account both the radius of the loop and the distance from the center. Now, what happens when we consider a point far away from the loop? What does this suggest?

Student 3
Student 3

We can ignore the **R²** term in the denominator because **x** is much larger than **R**.

Teacher
Teacher

Precisely! So the magnetic field simplifies to **B ≈ \frac{µ_0 2m}{4πx^3}**. Why do you think this is significant?

Student 4
Student 4

It shows the magnetic field behaves like the electric field of a dipole at large distances.

Teacher
Teacher

Exactly! The similarities between electric and magnetic dipoles help us understand the nature of magnetism.

Differences Between Electric and Magnetic Dipoles

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

While we see similarities between magnetic and electric dipoles, there are also key differences. What do you think is the major difference?

Student 1
Student 1

An electric dipole consists of two charges, while a magnetic dipole is a single current loop.

Teacher
Teacher

Right! Moreover, magnetic monopoles are still hypothetical, whereas electric charges exist naturally. Does that clarify the concept?

Student 2
Student 2

Yes, and it makes me curious about how magnetism is influenced at the atomic level!

Teacher
Teacher

That's an insightful thought! Magnetism does arise from the intrinsic magnetic moments of particles like electrons and protons, independent of circulating currents!

Introduction & Overview

Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.

Quick Overview

The circular current loop behaves like a magnetic dipole, with a magnetic field that resembles that of an electric dipole at large distances.

Standard

This section focuses on the characteristics of a circular current loop as a magnetic dipole, specifically discussing how the magnetic field generated by the loop is similar to the electric field of an electric dipole. It outlines the formulae for the magnetic field produced by a circular loop and illustrates the analogy between magnetic and electric dipoles.

Detailed

Detailed Summary

In this section, we analyze the circular current loop as an elementary magnetic dipole. The core concept is recognizing that the magnetic field produced by a circular current loop at large distances mirrors the electric field of an electric dipole. The magnetic field

B due to a circular loop of radius R carrying a steady current I on its axis is given by the equation:

$$ B = \frac{µ_0 IR^2}{2(x^2 + R^2)^{3/2}} $$

where x is the distance from the center of the loop along the axis. For points far away from the loop, where x is much greater than R, the equation simplifies to:

$$ B \approx \frac{µ_0 2m}{4πx^3} $$

Here, m is the magnetic moment defined as m = I × A, where A is the area of the loop. This leads us to see that the loop operates similarly to an electric dipole, where the magnetic field behaves according to the same principles as the electric field of an electric dipole. Notably, while an electric dipole consists of two opposite charges, a magnetic dipole is represented solely by the current loop without magnetic monopoles known in nature.

This understanding is significant in the study of electromagnetism, showing the unified behavior of electric and magnetic phenomena through the analogous principles governing dipoles.

Youtube Videos

Current Loop as a Magnetic Dipole - Moving Charges and Magnetism | Class 12 Physics Ch 4 (2023-24)
Current Loop as a Magnetic Dipole - Moving Charges and Magnetism | Class 12 Physics Ch 4 (2023-24)
Circular current loop as a magnetic dipole - Class 12 Physics - Moving charges and magnetism
Circular current loop as a magnetic dipole - Class 12 Physics - Moving charges and magnetism
21) Circular current loop as a magnetic dipole| Moving charges and magnetism class 12 Physics #neet
21) Circular current loop as a magnetic dipole| Moving charges and magnetism class 12 Physics #neet
8. Current loop as a Magnetic Dipole | CBSE 12th | Physics handwritten notes #cbse
8. Current loop as a Magnetic Dipole | CBSE 12th | Physics handwritten notes #cbse
Class 12| 5.6: Current loop as a magnetic dipole
Class 12| 5.6: Current loop as a magnetic dipole
Circular Current Loop|Magnetic Dipole|NCERT|CBSE|Physics 12|Tamil|Muruga MP#murugamp#tamil#ncert
Circular Current Loop|Magnetic Dipole|NCERT|CBSE|Physics 12|Tamil|Muruga MP#murugamp#tamil#ncert
Magnetic dipole moment of current loop | Moving charges & magnetism | 12 Physics #cbse #umeshrajoria
Magnetic dipole moment of current loop | Moving charges & magnetism | 12 Physics #cbse #umeshrajoria
Circular Current Loop as Magnetic Dipole | Class 12 Physics Moving Charges and Magnetism
Circular Current Loop as Magnetic Dipole | Class 12 Physics Moving Charges and Magnetism
magnetic fields lines of solenoid #shorts #class10science #scienceexperiment
magnetic fields lines of solenoid #shorts #class10science #scienceexperiment
Moving Charges n Magnetism 14 : Magnetic Moment :Current Loop as Magnetic Dipole : JEE/NEET
Moving Charges n Magnetism 14 : Magnetic Moment :Current Loop as Magnetic Dipole : JEE/NEET

Audio Book

Dive deep into the subject with an immersive audiobook experience.

Magnetic Field of a Current Loop

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

In this section, we shall consider the elementary magnetic element: the current loop. We shall show that the magnetic field (at large distances) due to current in a circular current loop is very similar in behaviour to the electric field of an electric dipole. In Section 4.5, we have evaluated the magnetic field on the axis of a circular loop, of a radius R, carrying a steady current I. The magnitude of this field is

B = \frac{\mu_0 I R^2}{2(x^2 + R^2)^{3/2}}

and its direction is along the axis and given by the right-hand thumb rule. Here, x is the distance along the axis from the centre of the loop. For x >> R, we may drop the R^2 term in the denominator. Thus,

B = \frac{\mu_0 I R^2}{2x^3}

Note that the area of the loop A = \pi R^2. Thus,

B = \frac{\mu_0 I A}{2\pi x^3}

Detailed Explanation

This chunk explains how a circular current loop behaves like a small magnet, producing a magnetic field similar to that of an electric dipole. When a current flows through this loop, it generates a magnetic field that can be calculated based on its radius and the current's strength. At points far away from the loop (when the distance x is much greater than the radius R), the formula simplifies to show how the magnetic field diminishes with distance. Here, the area of the loop is also defined, which is crucial for calculating the magnetic moment.

Examples & Analogies

Imagine a hula hoop that represents our current loop. When you give it a spin (representing the current), a wind circulates around it. If you move far away from the hula hoop, the wind (magnetic field) feels less intense, similar to how the magnetic field of the loop decreases with distance. This is akin to the way an electric dipole decreases in strength from a distance, like how the effect of a battery weakens as you move it away from a light bulb.

Magnetic Moment and Its Significance

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

As earlier, we define the magnetic moment m to have a magnitude

m = I A.

Hence,

B \approx \frac{\mu_0 m}{4\pi x^3}.

Detailed Explanation

In this chunk, we introduce the concept of the magnetic moment, which quantifies the strength and direction of a magnetic source. The magnetic moment for a current loop is calculated as the product of the current (I) and the area (A) of the loop. This definition plays an essential role in how we describe and analyze the behavior of magnetic fields produced by loops compared to electric charges.

Examples & Analogies

Think of a spinning top. The faster it spins (analogous to a higher current), the more stable and prominent its spinning motion becomes (representing a stronger magnetic moment). A larger spinning top (representing a larger area) also shows a stronger spin compared to a small top. This analogy helps to understand how the magnetic moment encompasses both current and area: a larger loop with more current would create a stronger 'spin' in the magnetic field it produces.

Comparing Electric Dipoles and Magnetic Dipoles

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

The expression of Eq. [4.25(a)] is very similar to an expression obtained earlier for the electric field of a dipole. The similarity may be seen if we substitute,

µ → 1/ε₀.

Detailed Explanation

Here, the chunk draws a comparison between electric dipoles and magnetic dipoles, suggesting that both behave similarly in terms of the fields they produce at distances. By replacing the magnetic properties with electric ones, we see how their fields display a compatible mathematical structure. This is significant because it indicates that the behavior of electric and magnetic fields may share underlying principles despite their fundamental differences.

Examples & Analogies

Consider the way a pair of balloons can behave as dipoles when charged. They create an area of influence around them similar to electric and magnetic fields. Just as you can visualize electrical charges attracting or repelling, the way circulating currents in a magnetic dipole can be visualized shows that underlying these phenomena are similar concepts of field strengths, just manifesting in different physical forms.

Characteristics of Magnetic Monopoles

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

Note, however, a fundamental difference: an electric dipole is built up of two elementary units — the charges (or electric monopoles). In magnetism, a magnetic dipole (or a current loop) is the most elementary element. The equivalent of electric charges, i.e., magnetic monopoles, are not known to exist.

Detailed Explanation

This chunk highlights the essential distinction between electric and magnetic dipoles. While electric dipoles consist of two opposing charges (positive and negative), magnetic dipoles arise from loops of current which do not have individual magnetic 'monopole' charges. Instead, every magnetic field observed is a dipole field, spinning between two poles—not within one pole, which is unique to magnetism.

Examples & Analogies

Imagine a pair of dice (representing electric charges) where one is red (positive) and the other blue (negative), showing how they work together in pairs as monopoles. In contrast, a magnetic dipole is like a bar magnet: you can't isolate one end of it without losing its magnetic property—every time you cut a magnet, you end up with two smaller magnets instead of a 'north' or 'south' monopole, illustrating the lack of independent magnetic charges.

Definitions & Key Concepts

Learn essential terms and foundational ideas that form the basis of the topic.

Key Concepts

  • Magnetic Moment: The measure of the strength and direction of a magnetic source.

  • Magnetic Field of Current Loop: The magnetic field produced by a circular current loop resembles that of an electric dipole at large distances.

  • Dipole Analogy: Magnetic dipoles operate similarly to electric dipoles but consist solely of current loops without distinct positive or negative charges.

Examples & Real-Life Applications

See how the concepts apply in real-world scenarios to understand their practical implications.

Examples

  • Calculating the magnetic moment of a circular current loop with a radius of 0.1 m and a current of 5 A results in m = Ia = (5 A)(π(0.1 m)^2) = 0.0157 A m².

  • Using the magnetic field formula at a point on the axis of the loop, B = (µ₀IR²)/(2(R² + x²)^(3/2)), with R = 0.1 m and I = 1 A for x significantly larger than R yields results consistent with the electric dipole equation.

Memory Aids

Use mnemonics, acronyms, or visual cues to help remember key information more easily.

🎵 Rhymes Time

  • Dipole, dipole, with strength so fine, for loops of current, the field will align.

📖 Fascinating Stories

  • Picture a circle of dancers, each holding a spark of energy; as they move, their magnetic field twirls around, resembling an electric dipole's power.

🧠 Other Memory Gems

  • To remember the magnetic moment formula: 'I-A' -> Imagine an 'I' (current) holding hands with an 'A' (area) forming a magnetic alliance!

🎯 Super Acronyms

M.I.C. - Magnetic Moment = I × A (Current times Area).

Flash Cards

Review key concepts with flashcards.

Glossary of Terms

Review the Definitions for terms.

  • Term: Magnetic Dipole

    Definition:

    A magnetic dipole is a magnetic configuration with a north and south magnetic pole with no net magnetic charge, typically represented by a current loop.

  • Term: Magnetic Moment

    Definition:

    The magnetic moment is a measure of the strength and orientation of a magnetic source, defined as m = I × A.

  • Term: Magnetic Field (B)

    Definition:

    The magnetic field around a magnet or current-carrying wire, represented in teslas (T), that exerts a force on moving charges.

  • Term: Electric Dipole

    Definition:

    An electric dipole consists of two equal and opposite charges separated by distance, creating an electric field.