Learn
Games

4.4 - MAGNETIC FIELD DUE TO A CURRENT ELEMENT, BIOT-SAVART LAW

Interactive Audio Lesson

Listen to a student-teacher conversation explaining the topic in a relatable way.

Biot-Savart Law Introduction

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Today, we’re going to learn how electrical currents produce magnetic fields, which is captured beautifully by the Biot-Savart law.

Student 1
Student 1

What is the Biot-Savart law?

Teacher
Teacher

The Biot-Savart law tells us that the magnetic field `dB` created by a small segment of current is proportional to the current `I`, the length of that segment `|dl|`, and it’s inversely proportional to the square of the distance from the segment to the point where we measure the field.

Student 2
Student 2

Does that mean that if we move further away, the magnetic field gets weaker?

Teacher
Teacher

Exactly! The relationship is like gravity where force weakens with distance. Also, remember the angle θ between the direction of the current and the displacement vector affects the strength of the magnetic field.

Student 3
Student 3

How do we find the direction of the magnetic field?

Teacher
Teacher

You can use the right-hand rule! If you point your thumb in the direction of the current and curl your fingers, they will point in the direction of the magnetic field lines.

Student 4
Student 4

Could you give us a quick reminder of that rule?

Teacher
Teacher

Sure! The right-hand rule helps us determine the direction of the magnetic field due to a current element. Just remember: thumb = current, fingers = field direction.

Teacher
Teacher

To recap, the Biot-Savart law shows how current creates magnetic fields with strength diminishing with distance, and we can find the direction using the right-hand rule.

Comparing Magnetic and Electric Fields

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Now let’s compare how electric fields created by static charges differ from magnetic fields produced by currents.

Student 1
Student 1

What are some key differences?

Teacher
Teacher

Good question! The electric field results from scalar sources, while magnetic fields are generated from vector sources, specifically currents. Also, while both fields can be influenced by the principle of superposition, magnetic fields depend on the angle between the current direction and the position vector.

Student 2
Student 2

So, if the current and the position vector are aligned, does that mean the magnetic field is zero?

Teacher
Teacher

Precisely! If `θ` is 0 or 180 degrees, the magnetic field `dB` becomes zero since sine of those angles is zero. That's why orientation matters in this context.

Student 3
Student 3

How about the direction of the field lines; are they similar?

Teacher
Teacher

Magnetic field lines form closed loops, unlike electric field lines which originate from positive charges and terminate at negative charges. This is a fundamental characteristic of magnetism.

Teacher
Teacher

Great job today! Remember, electric fields originate from static charges, while magnetic fields arise from moving charges, and their field lines behave differently.

Applications and Implications

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Let’s conclude by discussing how the principles we learned can apply practically in technology.

Student 1
Student 1

What are some devices that rely on these principles?

Teacher
Teacher

Devices like electric motors and generators rely heavily on magnetic fields created by currents. The Biot-Savart law helps design these systems.

Student 3
Student 3

That means electromagnetism is really important in our daily lives!

Teacher
Teacher

Absolutely! Electromagnetic principles underpin much of modern technology. Understanding how these fields interact allows us to innovate and improve devices we use every day.

Student 4
Student 4

Are there everyday examples we should remember?

Teacher
Teacher

Yes, think about how speakers convert electrical signals into sound using magnets. Or how magnetic locks operate based on current flowing through a wire. Very cool applications!

Teacher
Teacher

To wrap up, we’ve seen the significance of magnetic fields in both theory and application. Electromagnetism shapes our technology and everyday life!

Introduction & Overview

Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.

Quick Overview

This section discusses the relationship between electrical currents and the magnetic fields they generate, particularly through the Biot-Savart law.

Standard

The section details how a current element produces a magnetic field around it, introduces the Biot-Savart law, and compares it to Coulomb's law for electric fields. It explains the direction of the magnetic field in relation to the current and the displacement vector, emphasizing the right-hand rule for determining field orientation.

Detailed

Detailed Summary

In this section, we explore the principles behind the generation of magnetic fields by current-carrying conductors. The fundamental relationship is illustrated through the Biot-Savart Law, which quantifies the magnetic field (dB) produced by an infinitesimal current element (Idl) at a point P, located at a distance r. According to the Biot-Savart Law, the magnetic field is directly proportional to the current I and the length of the element |dl|, and inversely proportional to the square of the distance r from the element, represented mathematically as:

Code Editor - markdown

Where the direction of dB is perpendicular to the plane formed by I * dl and the displacement vector r. The significance of this law parallels Coulomb's law, where the electric field is generated by static charges. Differences include the vector nature of the current element and the angular dependency observed in magnetic fields.

The law also implies that if the magnetic field's direction is zero due to the angle θ being zero or 180 degrees, meaning the current is aligned directly with the line connecting the charge to the field point. The section also introduces the concept of magnetic field lines created by current elements, helping visualize magnetic phenomena. The magnetic field is explained further through the context of various configurations of wires and how they affect the magnetic field in surrounding space.

Youtube Videos

Biot-Savart Law|| Magnetic Effects of Current and Magnetism|| Animated hindi explanation || Physics
Biot-Savart Law|| Magnetic Effects of Current and Magnetism|| Animated hindi explanation || Physics
Biot Savart law (vector form) | Moving charges & magnetism | Khan Academy
Biot Savart law (vector form) | Moving charges & magnetism | Khan Academy
Moving Charges and Magnetism 01 : Biot-Savart Law : Magnetic Field due to Straight Wire JEE/NEET
Moving Charges and Magnetism 01 : Biot-Savart Law : Magnetic Field due to Straight Wire JEE/NEET
Biot Savart Law - Moving Charges and Magnetism | Class 12 Physics Chapter 4 (2023-24)
Biot Savart Law - Moving Charges and Magnetism | Class 12 Physics Chapter 4 (2023-24)
ONE SHOT - MOVING CHARGES & MAGNETISM | All Concepts & PYQs covered for NEET 2025 SUCCESS
ONE SHOT - MOVING CHARGES & MAGNETISM | All Concepts & PYQs covered for NEET 2025 SUCCESS
Biot Savart's Law, Chapter 4, Moving Charges and Magnetism, Class 12 Physics
Biot Savart's Law, Chapter 4, Moving Charges and Magnetism, Class 12 Physics
magnetic fields lines of solenoid #shorts #class10science #scienceexperiment
magnetic fields lines of solenoid #shorts #class10science #scienceexperiment

Audio Book

Dive deep into the subject with an immersive audiobook experience.

Introduction to Magnetic Field from a Current Element

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

All magnetic fields that we know are due to currents (or moving charges) and due to intrinsic magnetic moments of particles.
Here, we shall study the relation between current and the magnetic field it produces. It is given by the Biot-Savart’s law.

Detailed Explanation

Magnetic fields are created whenever there are currents or moving charges. One of the fundamental principles that describe how currents generate magnetic fields is the Biot-Savart law. This law helps us understand the relationship between an electrical current and the resulting magnetic field. Essentially, it states that each small segment of the current-carrying wire (referred to as a current element) contributes to the overall magnetic field at a certain point in space.

Examples & Analogies

Think of a water hose. When you turn it on and point it in different directions, the flow of water creates splashes in specific areas. Similar to how the water moves through the hose, when electricity flows through a wire, it creates a magnetic field that radiates outwards from each part of the wire regardless of its shape.

Biot-Savart Law Explained

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

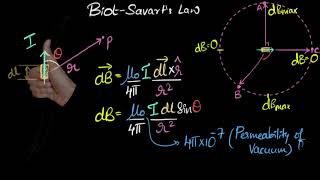
Fig. 4.7 shows a finite conductor XY carrying current I. Consider an infinitesimal element dl of the conductor. The magnetic field dB due to this element is to be determined at a point P which is at a distance r from it. Let θ be the angle between dl and the displacement vector r. According to Biot-Savart’s law, the magnitude of the magnetic field dB is proportional to the current I, the element length |dl|, and inversely proportional to the square of the distance r. Its direction is perpendicular to the plane containing dl and r. Thus, in vector notation, dB ∝ (I dl × r)/(r^3).

Detailed Explanation

The Biot-Savart law mathematically specifies how to calculate the magnetic field generated by a small section of current-carrying conductor. The strength of the magnetic field (dB) created depends on three factors: the amount of current (I) flowing through the wire segment, the length of that segment (dl), and the distance (r) from the segment to the point where the magnetic field is being measured. Additionally, the direction of the magnetic field is determined by the shape of the conductor segment and the angle between the segment and the observation point, making it a vector quantity.

Examples & Analogies

Imagine the way a fan generates airflow. The electric current runs through the wires of the fan motor, causing the blades to spin and generate wind. Here, you can visualize that each blade acts as a small current element contributing to the overall airflow, much like how each segment of wire contributes to the magnetic field.

Magnetic Field Characteristics

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

The magnitude of this field is, dB = (μ₀/4π) * (I dl sin θ)/r², where we have used the property of cross-product. The above expression holds when the medium is vacuum.

Detailed Explanation

This specific formulation of the Biot-Savart law indicates that the magnetic field due to a small wire segment directly relates to the current flowing, the length of that segment, and importantly, inversely to the square of the distance from that segment. This relationship is crucial in understanding how magnetic fields weaken with distance, similar to how light from a bulb becomes dimmer the farther you stand away.

Examples & Analogies

Think of a flashlight. When you shine it close to an object, the light is bright. But as you move away, the brightness diminishes quickly. Similarly, as we move further from a current-carrying wire, the influence of its magnetic field reduces significantly.

Permeability of Free Space

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

The proportionality constant in SI units has the exact value, μ₀ = 10⁻⁷ T m/A. We call μ₀ the permeability of free space (or vacuum).

Detailed Explanation

The permeability of free space, μ₀, is a fundamental constant in electromagnetism. It quantifies the ability of a vacuum to support the formation of magnetic fields. It's not just a fixed number; it is foundational to many equations in physics, particularly in relation to inductance and magnetic fields produced by various sources.

Examples & Analogies

Consider how a musical instrument uses air to create sound. The quality and speed of the sound depend heavily on the characteristics of the air in the room. Similarly, the constant μ₀ determines how magnetic fields behave in a vacuum and sets the stage for how they interact with materials and electric currents.

Comparison to Electrostatic Fields

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

The Biot-Savart law for the magnetic field has certain similarities, as well as, differences with the Coulomb’s law for the electrostatic field...

Detailed Explanation

The Biot-Savart law for magnetic fields is analogous to Coulomb's law for electric fields. Both laws describe how fields are created by source elements, but there are notable differences. Coulomb’s law is based on scalar quantities (charges), while the Biot-Savart law involves vector quantities (current elements). Additionally, magnetic fields are always perpendicular to the current direction, unlike electric fields.

Examples & Analogies

If we think of electrical charges as sources of light, those charges would create light radiating outwards as lines. In contrast, magnetic currents are like wind swirling around a point, always changing direction and interacting differently with objects in their path.

Definitions & Key Concepts

Learn essential terms and foundational ideas that form the basis of the topic.

Key Concepts

  • Biot-Savart Law: Describes how a current element produces a magnetic field in space.

  • Direction of Magnetic Field: Determined using the right-hand rule, where the thumb indicates current direction and fingers show field direction.

  • Comparison with Electric Fields: Magnetic fields arise from moving charges, whereas electric fields come from static charges.

Examples & Real-Life Applications

See how the concepts apply in real-world scenarios to understand their practical implications.

Examples

  • A straight wire carrying 5 A of current produces a magnetic field that can be calculated using the Biot-Savart law at any point around it.

  • Iron filings arranged in concentric circles around a current-carrying wire illustrate the magnetic field pattern visually.

Memory Aids

Use mnemonics, acronyms, or visual cues to help remember key information more easily.

🎵 Rhymes Time

  • When a wire carries current by day, the magnetic field comes out to play.

📖 Fascinating Stories

  • Imagine a small wire carrying current, like a tiny boat in a sea of magnetic fields, creating ripples in the water as it moves along.

🧠 Other Memory Gems

  • CIRCLES for Current Induces Right-handed Circles, Leading to Effective Strength.

🎯 Super Acronyms

MICE - Magnetic Influence from Current Elements.

Flash Cards

Review key concepts with flashcards.

Glossary of Terms

Review the Definitions for terms.

  • Term: BiotSavart Law

    Definition:

    A fundamental principle that explains how electric currents produce magnetic fields in space.

  • Term: Magnetic Field (B)

    Definition:

    A vector field that describes the magnetic influence exerted by electric charges or currents.

  • Term: Current Element (Idl)

    Definition:

    An infinitesimal segment of wire carrying current, used in calculations of magnetic fields.

  • Term: Sine of Angle (sinθ)

    Definition:

    A mathematical function relating the angle to the proportion of the opposite side over the hypotenuse in a right triangle; used in context with magnetic fields.