Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Torque
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will discuss how a rectangular current loop behaves when it is placed in a uniform magnetic field. Can anyone recall what happens to a current-carrying conductor in a magnetic field?
The current creates a magnetic field around it.
Correct! And when we have a loop, the forces acting on different sides can produce a torque. This torque is what enables the loop to rotate. Letβs explore how we can calculate this torque. What is torque, by the way?
Torque is a measure of how much a force acting on an object causes that object to rotate.
Exactly! The formula for torque is Ο = F Γ d, where F is the force and d is the distance from the pivot. In our case, however, we have a rectangular loop. Letβs delve deeper into how the forces on each side of the loop contribute to the overall torque.
Forces on the Loop
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
When the rectangular loop is in a magnetic field, forces F1 and F2 act on arms AB and CD, respectively, which are perpendicular to the magnetic field. How do you think this affects the loop?
Well, if the forces are unequal, they might cause the loop to rotate.
Right! However, in this case, the forces on sides AD and BC cancel each other out, resulting in a net zero force, but we still have a torque about the pivot. The magnitude of torque can be expressed as Ο = IABsinΞΈ. Why do we include the sine term?
The sine term accounts for the angle between the magnetic field and the area vector of the loop.
Exactly! As the angle changes, so does the torque on the loop. Now, what happens when the plane of the loop is aligned with the magnetic field?
Conditions for Maximum and Zero Torque
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
The torque on the loop is maximum when sinΞΈ equals 1, meaning the angle ΞΈ is 90 degrees. Conversely, what happens when the angle is 0 or 180 degrees?
Then sinΞΈ is zero, and so the torque is also zero.
Does that mean the loop won't rotate?
Precisely! When the magnetic moment is parallel or antiparallel to the magnetic field, there is no torque acting on the loop. This alignment is crucial to understand magnetic stability. Who can explain why the magnetic moment indicates the direction of the loop's rotation?
The magnetic moment points in the direction of the magnetic field, so the loop will try to align with it.
Excellent! You all are grasping these concepts well. Remember that the loop acts similarly to an electric dipole in an electric field. Understanding this analogy can help with future studies in electromagnetism.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explain how a rectangular current loop in a uniform magnetic field experiences torque due to the interaction of magnetic forces on its arms, while the net force remains zero. Additionally, the section draws parallels with electric dipoles and further explores the effects of varying angles between the loop and magnetic field.
Detailed
Torque on Current Loops in Magnetic Fields
The section begins by establishing that a rectangular loop carrying a steady current experiences a torque when placed in a uniform magnetic field. It highlights that the net force on the loop is zero due to equal and opposite forces acting on pairs of opposite sides, thus resulting in torque but no translational motion. The mathematical representation of torque, as well as its analogy to electric dipoles, is presented. The torque is calculated based on the product of the current, area of the loop, and the magnetic field, modulated by the sine of the angle between the magnetic field and the normal to the loop. Additionally, we see how the torque is affected by changing angles, with a focus on the conditions under which torque becomes zeroβnamely when the magnetic moment and magnetic field are aligned or anti-aligned. This section concludes by discussing the implications of these principles in understanding magnetic dipoles and their behavior in magnetic fields.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Torque on a Current Loop
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We now show that a rectangular loop carrying a steady current I and placed in a uniform magnetic field experiences a torque. It does not experience a net force. This behaviour is analogous to that of electric dipole in a uniform electric field.
Detailed Explanation
When a rectangular loop carrying current is placed in a uniform magnetic field, it experiences a force but no net linear force. This is because the forces acting on opposite sides of the loop cancel each other out. Instead of moving linearly, the loop attempts to rotate, which results in torque. Torque is essentially a twisting force that causes the loop to rotate around an axis. This behavior is similar to how an electric dipole behaves in an electric field.
Examples & Analogies
Think of a door that is pushed at one side. If you push at the hinge side, it wonβt move much sideways, but if you push at the opposite side, it will swing open. Similarly, the magnetic forces on the loop create a torque that attempts to rotate the loop rather than pushing it in a straight line.
Force on the Rectangular Loop
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We first consider the simple case when the rectangular loop is placed such that the uniform magnetic field B is in the plane of the loop. This is illustrated in Fig. 4.18(a). The field exerts no force on the two arms AD and BC of the loop. It is perpendicular to the arm AB of the loop and exerts a force F on it which is directed into the plane of the loop.
Detailed Explanation
In this specific arrangement, the uniform magnetic field does not exert any force on the arms of the loop parallel to the magnetic field (AD and BC), as thereβs no current perpendicular to those arms. However, for the arms perpendicular to the field (AB and CD), a magnetic force is exerted. The force on arm AB points into the plane, while the force on arm CD points out of the plane, creating a couple that results in torque around the axis of rotation.
Examples & Analogies
Imagine holding a paper clip in a uniform magnetic field. If the paper clip is oriented correctly, forces can cause it to either lift off the table or rotate depending on how the current runs through it, similar to the way these forces act on the rectangular loop. Each arm acts like a lever, causing it to spin rather than translate.
Calculating Torque Magnitude
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Thus, the net force on the loop is zero. There is a torque on the loop due to the pair of forces F and F. The torque is (in magnitude) t = IbB = I A B.
Detailed Explanation
The total force on the loop becomes zero as opposite forces negate each other, but the presence of a torque remains significant. The torque can be quantified by multiplying the current (I), the length of the loop (b), and the magnetic field strength (B). This results in the formula for torque: Ο = IAB, where A is the area of the loop. This formula quantifies how effective the loopβs current is at experiencing rotational motion within the magnetic field.
Examples & Analogies
Visualize helps to lift a heavy door by pushing on the handle. The further you push from the hinges (the axis), the easier it is to swing the door open. Likewise, in this case, the effectiveness of the current loop in generating torque increases with the area of the loop and the strength of the magnetic field.
Torque at an Angle
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
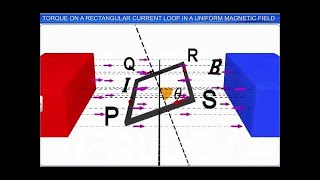
We next consider the case when the plane of the loop is not along the magnetic field, but makes an angle ΞΈ with it. The forces on the arms BC and DA are equal, opposite, and act along the axis of the coil, which connects the centres of mass of BC and DA.
Detailed Explanation
When the loop is tilted at an angle ΞΈ to the magnetic field, the calculation of torque changes as now the forces are no longer purely vertical or horizontal. The torque depends on the sine of the angle between the magnetic moment vector and the magnetic field, resulting in the formula: Ο = IAB sin(ΞΈ). As the angle changes from 0 to 90 degrees, the torque will also change, reaching a maximum when sin(ΞΈ) is maximized at ΞΈ = 90 degrees.
Examples & Analogies
This can be compared to a wind turbine. The blades catch the wind at an angle to be most effective. If the blades are aligned perfectly with the wind, they wonβt rotate at all. Similarly, aligning at the right angle to the magnetic field ensures the best torque effect on the current loop.
Definitions and Applications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We define the magnetic moment of the current loop as m = I A, where the direction of the area vector A is given by the right-hand thumb rule and is directed into the plane of the paper.
Detailed Explanation
The magnetic moment is a vector quantity that defines the strength and direction of a loop's ability to align in a magnetic field. It is calculated as the product of the current flowing in the loop (I) and the area of the loop (A). The direction of this vector follows the right-hand rule, which helps visualize the orientation of this magnetic moment in relation to the magnetic field.
Examples & Analogies
This is similar to how a compass needle behaves. The magnetic moment directs like the compass needle aligns with the Earth's magnetic field, pointing north. The strength of the needleβs alignment depends on how strong the magnetic field is, similar to how a current loop will orient itself in an external magnetic field.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Torque is generated by the forces acting on the arms of a rectangular current loop in a magnetic field.
-
The magnetic moment determines the direction and magnitude of torque experienced by a loop.
-
Torque becomes zero when the magnetic moment is aligned with the magnetic field.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A rectangular loop of wire carrying a current in a magnetic field will experience torque, causing it to rotate, while the forces acting on opposite arms balance out to maintain net-zero force.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
When loops in fields do sway, torque can guide their way.
π Fascinating Stories
-
Imagine a loop trying to stand tall in a magnetic field, sometimes twisting and turning as it tries to align perfectly. Torque helps it know when it's okay to stop and when to keep rotating!
π§ Other Memory Gems
-
For calculating torque: 'I Add B, Sine the Angle' - remember I, A, B, and the sine function!
π― Super Acronyms
TAP - Torque, Area, and Perpendicular Angle.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Torque (Ο)
Definition:
A measure of the rotational force acting on an object, causing it to rotate about an axis.
-
Term: Magnetic Moment (m)
Definition:
A vector quantity that determines the torque experienced by a current loop in a magnetic field.
-
Term: Current Loop
Definition:
A closed conducting path in which an electric current flows, creating a magnetic field.
-
Term: Uniform Magnetic Field
Definition:
A magnetic field that has the same strength and direction at all points in space.
-
Term: Angular Position (ΞΈ)
Definition:
The angle between the magnetic field direction and the normal to the plane of the loop.