Learn
Games

4.3 - MOTION IN A MAGNETIC FIELD

Interactive Audio Lesson

Listen to a student-teacher conversation explaining the topic in a relatable way.

Understanding Motion in Magnetic Fields

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Today, we're going to discuss how charged particles move in a magnetic field. Can anyone tell me what happens to a charged particle when it enters a magnetic field?

Student 1
Student 1

Does it change direction?

Teacher
Teacher

Exactly! The force exerted by the magnetic field is always perpendicular to the velocity of the particle, which changes its direction but not its speed. So, it moves in a curved path.

Student 2
Student 2

So it would make a circle if it goes directly into the field?

Teacher
Teacher

Correct! This perpendicular force acts as a centripetal force. We'll derive the equation for the radius of that circular path shortly. Remember the acronym 'RAMP' - Radius equals Affects of magnetic Particle charge.

Student 3
Student 3

Why doesn't the magnetic force do any work on the particle?

Teacher
Teacher

Great question! Because the magnetic force is perpendicular to the velocity, it doesn't change the kinetic energy of the particle, which means no work is done. Let's consider how this applies when a particle has a velocity component along the magnetic field, leading to helical motion.

Deriving Motion Parameters

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Now, let’s explore how we can calculate the radius of the circular path. We know that the required centripetal force is related to mass and velocity. How do we relate this with the magnetic force?

Student 3
Student 3

Is it because the magnetic force provides that necessary centripetal force?

Teacher
Teacher

Exactly! The equation we use is F = m(v^2/r), which equals qvB for magnetic force. Thus, combining these gives us the equation for radius, r = mv/(qB).

Student 2
Student 2

Does this mean that a faster particle will have a bigger radius?

Teacher
Teacher

That's right! As the speed increases, the radius of the circular path also increases. So just remember, a high velocity means a larger radius.

Student 1
Student 1

And if the charge increases, the radius also increases, right?

Teacher
Teacher

Exactly! The relationship is linear concerning mass and charge, which is essential to remember for future applications.

Helical Motion and Applications

Unlock Audio Lesson

Signup and Enroll to the course for listening the Audio Lesson

Teacher
Teacher

Let's talk about helical motion. When a charged particle moves with a component of its velocity parallel to the magnetic field, what kind of path does it take?

Student 4
Student 4

It would spiral around the direction of the field!

Teacher
Teacher

Exactly that! The particle combines circular motion perpendicular to the magnetic field with linear motion parallel to it, creating a helix. To summarize, as it rotates, we can also look at the pitch of this helix.

Student 1
Student 1

What do we calculate the pitch with?

Teacher
Teacher

Great question! The pitch 'p' is calculated as v_parallel × T, the time period of one rotation. So knowing the angular speed, we can compute it easily.

Student 3
Student 3

So we can apply this in cyclotron designs, right?

Teacher
Teacher

Absolutely! Understanding these dynamics is critical in designing particle accelerators like cyclotrons.

Introduction & Overview

Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.

Quick Overview

This section discusses the dynamics of charged particles moving in magnetic fields, focusing on the principles of motion and the effects of magnetic forces.

Standard

The section elaborates on how charged particles behave in the presence of magnetic fields, emphasizing that the magnetic force acts perpendicularly to their velocity, resulting in circular or helical motion. Key concepts include the derivation of the radius of circular motion and the roles of speed and magnetic field strength in determining particle dynamics.

Detailed

Motion in a Magnetic Field

In this section, we explore the impact of magnetic fields on moving charged particles. The magnetic force experienced by a charged particle is perpendicular to its velocity, which means that while the particle's speed remains constant, its direction changes, leading to circular or helical trajectories. For a particle moving perpendicular to a uniform magnetic field, the magnetic force acts as a centripetal force, and the radius of the circle can be derived from the balance between the centripetal force and the magnetic force.

When the velocity of the charged particle has a component along the magnetic field, this component remains unchanged, resulting in a helical path. The section also outlines the formulas derived for the radius of the circular motion and the frequency of rotation, emphasizing that the angular frequency depends only on the charge, mass, and magnetic field strength. These principles are crucial for understanding the application of magnetic fields in devices like cyclotrons.

Youtube Videos

Motion in a Magnetic Field - Moving Charges And Magnetism - Class 12 Science (Physics Part 1)
Motion in a Magnetic Field - Moving Charges And Magnetism - Class 12 Science (Physics Part 1)
Motion of charge in magnetic field | Moving charges and magnetism | 12 Physics #cbse
Motion of charge in magnetic field | Moving charges and magnetism | 12 Physics #cbse
Moving Charges n Magnetism 08 : Motion of a charged Particle in Magnetic Field : JEE /NEET
Moving Charges n Magnetism 08 : Motion of a charged Particle in Magnetic Field : JEE /NEET
Class 12 physics notes | Moving charges and magnetism | pdf link in the description | JEE | #shorts
Class 12 physics notes | Moving charges and magnetism | pdf link in the description | JEE | #shorts
12th class physics chapter 4 moving charges and magnesium one shot PW..
12th class physics chapter 4 moving charges and magnesium one shot PW..
Moving Charges and Magnetism || Complete chapter explanation || Class 12th physics ||
Moving Charges and Magnetism || Complete chapter explanation || Class 12th physics ||
Moving charge and magnetism #animation #short #movingchargesandmagnetism #physics #12thphysics
Moving charge and magnetism #animation #short #movingchargesandmagnetism #physics #12thphysics
Moving Charges and Magnetism Class 12 Physics: Motion of Charged Particle in Magnetic Field | BYJU'S
Moving Charges and Magnetism Class 12 Physics: Motion of Charged Particle in Magnetic Field | BYJU'S
Toroid Magnetic field Animation #3danimation #physic #12thphysics #fundamentalphysics #shorts
Toroid Magnetic field Animation #3danimation #physic #12thphysics #fundamentalphysics #shorts

Audio Book

Dive deep into the subject with an immersive audiobook experience.

Work Done by Magnetic Force

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

We will now consider, in greater detail, the motion of a charge moving in a magnetic field. We have learnt in Mechanics (see Class XI book, Chapter 5) that a force on a particle does work if the force has a component along (or opposed to) the direction of motion of the particle. In the case of motion of a charge in a magnetic field, the magnetic force is perpendicular to the velocity of the particle. So no work is done and no change in the magnitude of the velocity is produced (though the direction of momentum may be changed).

Detailed Explanation

When a charged particle moves in a magnetic field, the force exerted by the field acts perpendicular to the direction of the particle's motion. This means it doesn't work to change the speed of the particle but can change its direction. In mechanics, work is done when a force acts in the same direction as the motion. So the magnetic force doesn't contribute to work, meaning the kinetic energy (or speed) of the particle remains constant.

Examples & Analogies

Think about a car moving in a circular path on a flat surface. Although the car is constantly changing direction (hence, experiencing acceleration), its speed can stay the same if there is no gas pedal pushed or brake applied. The steering wheel directs the car, similarly to how a magnetic field can direct a charged particle.

Circular Motion of Charges

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

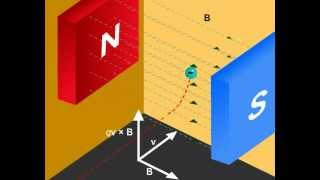
We shall consider motion of a charged particle in a uniform magnetic field. First, consider the case of v perpendicular to B. The perpendicular force, q v × B, acts as a centripetal force and produces a circular motion perpendicular to the magnetic field. The particle will describe a circle if v and B are perpendicular to each other.

Detailed Explanation

When a charged particle moves perpendicularly to a magnetic field, the magnetic force acts like centripetal force, pulling it toward the center of a circle. The particle thus follows a circular path due to this consistent force. This relationship is crucial in many devices, such as cyclotrons, designed to accelerate charged particles along circular paths.

Examples & Analogies

Imagine a child swinging a ball on a string around in a circle. The tension in the string acts as the centripetal force keeping the ball moving in its circular path. If the child lets go of the string, the ball will fly off in a straight line tangential to the circle. Similarly, a charged particle experiences circular motion in a magnetic field due to the magnetic force acting as the tension in the string.

Helical Motion of Charges

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

If velocity has a component along B, this component remains unchanged as the motion along the magnetic field will not be affected by the magnetic field. The motion in a plane perpendicular to B is as before a circular one, thereby producing a helical motion.

Detailed Explanation

When a charged particle has velocity both perpendicular and parallel to a magnetic field, it moves in a helix. The component of velocity parallel to the magnetic field remains unchanged, allowing the particle to move along the direction of the field while also circulating due to the perpendicular component. The resulting path is a spiral or helix independent of the speed of the particle.

Examples & Analogies

Consider a corkscrew moving through a piece of wood. As you turn the corkscrew, it moves both down into the wood and also rotates in circles. In the same way, a charged particle moves along a helical path, combining forward motion and circular motion.

Radius of Circular Motion

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

You have already learnt in earlier classes (See Class XI, Chapter 3) that if r is the radius of the circular path of a particle, then a force of m v² / r, acts perpendicular to the path towards the centre of the circle, and is called the centripetal force. If the velocity v is perpendicular to the magnetic field B, the magnetic force is perpendicular to both v and B and acts like a centripetal force. It has a magnitude q v B. Equating the two expressions for centripetal force, m v²/r = q v B, which gives r = m v / qB for the radius of the circle described by the charged particle.

Detailed Explanation

Understanding the balance between centripetal force and the magnetic force allows us to determine the radius of the circular path traveled by a charged particle in a magnetic field. The two forces being equal means that the mass of the particle, its speed, and the magnetic field strength will dictate how large or small the radius of motion will be.

Examples & Analogies

Think of the way a planet orbits a star. The gravity (centripetal force) keeps it in a circular path. If a planet were to move faster, it would need more gravitational pull to keep it in the same orbit. If it were lighter, it might spiral outwards. Similarly, for charged particles in a magnetic field, the strength of the magnetic field and the properties of the particle control how tightly it curves.

Cyclotron Frequency

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

If ω is the angular frequency, then v = ω r. So, ω = 2π ν = q B / m, which is independent of the velocity or energy. Here, ν is the frequency of rotation. The independence of ν from energy has important application in the design of a cyclotron.

Detailed Explanation

The angular frequency of a particle in a magnetic field is defined by the relationship between its charge, the strength of the magnetic field, and its mass. Notably, this frequency doesn't change with the energy of the particle, meaning that regardless of how fast or how much energy it acquires, the rate at which it spirals remains consistent. This principle is essential for devices like cyclotrons that manipulate charged particles for experiments or medical applications.

Examples & Analogies

Imagine a Ferris wheel. No matter how fast or slow you go on the Ferris wheel, the time it takes to complete one rotation depends on the wheel's size and the force used to turn it, similar to how the charge and magnetic field affect a charged particle's rotational frequency.

Pitch of Helical Motion

Unlock Audio Book

Signup and Enroll to the course for listening the Audio Book

The time taken for one revolution is T = 2π/ω. If there is a component of the velocity parallel to the magnetic field (denoted by v||), it will make the particle move along the field, and the path of the particle would be a helical one. The distance moved along the magnetic field in one rotation is called pitch p. Using the relation p = vT, we find that p = v|| (2πm / (qB)).

Detailed Explanation

The pitch refers to how far a charged particle moves along the direction of the magnetic field during one complete circular rotation. By understanding the relationship between the time of rotation and the component of velocity parallel to the field, we can quantify how quickly the charge moves away from its starting point along the field.

Examples & Analogies

Picture a screw going into a board. The pitch is like how far the screw penetrates the board with each full turn. Similarly, in the helical motion of a charged particle, the pitch indicates how far it moves parallel to the magnetic field with each circular orbit.

Definitions & Key Concepts

Learn essential terms and foundational ideas that form the basis of the topic.

Key Concepts

  • Charged Particles: Particles that carry an electric charge, which can be influenced by electric and magnetic fields.

  • Magnetic Force: The force acting on a charged particle in a magnetic field that is perpendicular to its velocity, resulting in circular motion.

  • Centripetal Force: The inward force necessary to keep an object in a circular path, provided by the magnetic force in this context.

  • Helical Motion: The motion of a charged particle that moves linearly along with its axial component, while revolving around the field lines.

Examples & Real-Life Applications

See how the concepts apply in real-world scenarios to understand their practical implications.

Examples

  • An electron moving perpendicular to a magnetic field describes a circular path due to the magnetic Lorentz force acting on it.

  • A proton moving at high speed in a magnetic field exhibits helical trajectory because it possesses a velocity component parallel to the field as well.

Memory Aids

Use mnemonics, acronyms, or visual cues to help remember key information more easily.

🎵 Rhymes Time

  • Magnetic motion is quite a show, with paths curving in a flowing flow.

📖 Fascinating Stories

  • Imagine a child on a merry-go-round. Though they change direction, their speed stays the same, just like a charged particle in a magnetic field.

🧠 Other Memory Gems

  • Remember 'CIRCLE': Charge In Radius Can Lead to Energy impact by B field.

🎯 Super Acronyms

Use 'HELO' for 'Helical Energy Leads Outward' to remember helical motion concepts.

Flash Cards

Review key concepts with flashcards.

Glossary of Terms

Review the Definitions for terms.

  • Term: Lorentz Force

    Definition:

    The total force experienced by a charged particle in electric and magnetic fields.

  • Term: Centipetal Force

    Definition:

    The net force required to keep an object moving in a circular path.

  • Term: Radius of Curvature

    Definition:

    The distance from the center of the circular path to the particle's path.

  • Term: Helical Motion

    Definition:

    A type of motion where an object moves in a spiral path around an axis.