Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Forces Between Currents
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will explore the interaction between two parallel currents. Can anyone tell me what happens when two wires carrying current are brought close together?
They either attract or repel each other, right?
Exactly! This phenomenon is due to the magnetic fields created by each current. Remember the right-hand rule to determine the direction of these fields. Can you explain how we use that rule?
We point our thumb in the direction of the current, and our fingers curl in the direction of the field.
Great! Remembering 'thumb points current, curl your fingers' can help you recall this easily. Now, let's look deeper into why the forces occur.
Attraction and Repulsion of Currents
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
If both currents flow in the same direction, they attract. What do you think happens if the currents flow in opposite directions?
They repel each other.
Correct! To visualize, think of how like magnetic poles interact. Both exact same situations cause different reactions. Can anyone summarize why this is so?
It\u2019s because the magnetic fields around them affect each other in opposite directions!
Exactly! This leads us to consider Ampere's law for calculating the force between these conductors.
Mathematical Expression of Force
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let\u2019s derive the expression for the force between two parallel wires. The force per unit length is given by the equation: F = \u03bc\u2080I\u2090I_b / (2\u03c0d). Who can define each term in this formula?
F is the force, \u03bc\u2080 is the permeability of free space, I\u2090 and I_b are the currents, and d is the distance between the wires.
Well done! This formula helps us quantify how strong the interaction is. Remembering, 'force depends on currents and distance' is a good way to recall it!
So, if the distance decreases, the force increases?
Exactly! As distance d decreases, the force increases due to the inverse relationship.
Applications and Implications
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Understanding these forces helps us in various applications. Can anyone mention an application of this knowledge?
Electromagnets, right?
Yes! Electromagnets use this principle to lift heavy objects. This knowledge is vital in designing electrical circuits too. Critical thinking here helps future engineers! Let\u2019s summarize our discussion.
So parallel currents attract, antiparallel repel, and their interaction can be calculated with a formula!
Exactly! That summarizes our key points, reinforcing the fundamental concepts. Well done, everyone!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore how two long parallel conductors carrying currents interact with each other. The section highlights Ampere's findings on the nature of these forces, explaining how parallel currents attract while antiparallel currents repel, solidifying the concepts through mathematical expressions and derivations.
Detailed
Detailed Summary\n\nIn this section, we examine the interactions between two long, parallel conductors that carry electric currents. According to Ampere's observations in the 1820s, each conductor produces a magnetic field that affects the other. The magnetic field created by conductor 'a' exerts a force on conductor 'b', and vice versa.\n\n## Key Points:\n- : When a current flows through a conductor, it generates a magnetic field around it. The direction of this field can be determined using the right-hand rule.\n- : If two currents in parallel conductors flow in the same direction, they attract each other. Conversely, if the currents flow in opposite directions, they repel each other. \n- : The force of interaction per unit length between two parallel currents, I_a and I_b, separated by a distance d, is given by the equation:\n \n $$ F = \frac{\mu_0 I_a I_b}{2\pi d} $$\n\n where \( \mu_0 \) is the permeability of free space.\n\nThese concepts illustrate how current-carrying conductors influence each other, laying the foundation for understanding electromagnetic forces.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Forces Between Currents
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We have learnt that there exists a magnetic field due to a conductor carrying a current which obeys the Biot-Savart law. Further, we have learnt that an external magnetic field will exert a force on a current-carrying conductor. This follows from the Lorentz force formula. Thus, it is logical to expect that two current-carrying conductors placed near each other will exert (magnetic) forces on each other. In the period 1820-25, Ampere studied the nature of this magnetic force and its dependence on the magnitude of the current, on the shape and size of the conductors, as well as, the distances between the conductors.
Detailed Explanation
In this chunk, we are introduced to the concept of magnetic forces acting between two parallel current-carrying conductors. The phenomenon arises from each conductor generating a magnetic field around it, and when they are placed near each other, these fields interact, causing forces. André-Marie Ampère conducted extensive studies during the early 1820s to explore these interactions, laying the groundwork for our understanding of electromagnetism. The interactions depend on several factors, including the current magnitudes in the conductors and their distances apart.
Examples & Analogies
Imagine two magnets with their north poles facing each other. Just like these magnets can either attract or repel based on their orientation, two parallel wires can either pull towards each other (attract) or push away from each other (repel) depending on the direction of the current flowing through them. This analogy helps illustrate how currents create forces similar to magnetic forces between magnets.
Magnetic Field Setup and Force Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
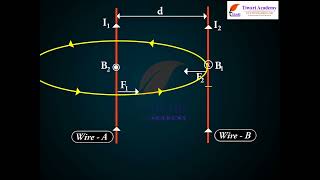
Figure 4.17 shows two long parallel conductors a and b separated by a distance d and carrying (parallel) currents I and I , respectively. The conductor βaβ produces the same magnetic field B at all points along the conductor βbβ. The right-hand rule tells us that the direction of this field is downwards (when the conductors are placed horizontally). Its magnitude is given by Eq. [4.15(a)] or from Ampereβs circuital law: m I B = 0 a 2p d. The conductor βbβ carrying a current I will experience a sideways force due to the field B . The direction of this force is towards the conductor βaβ. We label this force as F , the force on a segment L of βbβ due to βaβ. The magnitude of this force is given by Eq. (4.4), F = I LB.
Detailed Explanation
This portion discusses how two long parallel wires carrying currents interact with each other. As wire 'a' generates a magnetic field, wire 'b' feels this magnetic field and consequently experiences a force. The direction of the magnetic field can be determined using the right-hand rule: if you point your thumb in the direction of the current, your fingers will curl in the direction of the magnetic field. The force experienced by wire 'b' because of wire 'a' can be calculated using the formula for magnetic force, which is dependent on the current in both wires, their lengths, and the distance between them.
Examples & Analogies
Think of two long straight straws lying parallel to each other. If you blow air through one straw, it will create a moving air current. If you hold the other straw closely above the first straw, the air from the first straw can exert a pressure that either pushes the second straw away or pulls it closer depending on how you position them. Similarly, the moving electric charges create a magnetic force that can either attract or repel the wires.
Newtonβs Third Law and Current Interaction
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
It is of course possible to compute the force on βaβ due to βbβ. From considerations similar to above we can find the force F , on a segment of length L of βaβ due to the current in βbβ. It is equal in magnitude to F , and directed towards βbβ. Thus, F = βF . Note that this is consistent with Newtonβs third Law. Thus, at least for parallel conductors and steady currents, we have shown that the Biot-Savart law and the Lorentz force yield results in accordance with Newtonβs third Law.
Detailed Explanation
In this part, we explore the action-reaction pairs that arise when two currents interact. The force exerted by the current in wire 'a' on wire 'b' is equal in size and opposite in direction to the force exerted by wire 'b' on wire 'a'. This reflects Newton's Third Law, which states that for every action, there is an equal and opposite reaction. This reinforces the concept that magnetic interactions are reciprocal; the wires affect each other equally.
Examples & Analogies
Consider two people on skateboards pushing off each other: when one person pushes the other, they move away with an equal and opposite reaction. Just like in this scenario, the two wires exert forces on each other that are equal in strength but in opposite directions, demonstrating the same principle as Newton's law.
Attraction and Repulsion of Currents
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We have seen from above that currents flowing in the same direction attract each other. One can show that oppositely directed currents repel each other. Thus, Parallel currents attract, and antiparallel currents repel. This rule is the opposite of what we find in electrostatics. Like (same sign) charges repel each other, but like (parallel) currents attract each other.
Detailed Explanation
This chunk summarizes a pivotal concept in electrostatics and electromagnetism: the behavior of currents in terms of attraction and repulsion. When currents are in the same direction (parallel), they will attract each other due to the interaction of their magnetic fields. Conversely, when the currents flow in opposite directions (antiparallel), they will repel each other. This is very different from how electric charges interact, which tend to repel like charges and attract unlike charges.
Examples & Analogies
Imagine two people on a swing in a park. If both people are swinging towards each other, they are drawn to each other and can even collide (attraction). If one person swings towards, while the other swings away from them, it creates a push (repulsion). This captures the essence of how current behaves: the direction of the 'swing' determines whether they come together or move apart.
Definition of the Ampere
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let f represent the magnitude of the force F per unit length. Then, from Eq. (4.17), f = m I I 0 a b ba 2Οd. The above expression is used to define the ampere (A), which is one of the seven SI base units.
Detailed Explanation
In this final chunk, the force per unit length for the two parallel currents is mathematically defined, leading to the formal definition of the ampere, which is the base unit of electric current in the International System of Units (SI). The equation relates the force between two parallel conductors directly to the current flowing through them, which is a foundational principle in understanding how electricity is measured and how it behaves under magnetic influences.
Examples & Analogies
Think of the ampere like a standard weight you use when measuring ingredients in cooking. Just as you might define a cup as a specific measurement for flour, the ampere is the standardized measure for electric current based on the observable effects (forces) between two current-carrying wires, ensuring consistency in the measurement of electricity.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Magnetic Forces: Forces experienced between current-carrying conductors depend on their current directions.
-
Ampere's Law: A mathematical description of the magnetic forces between currents.
-
Magnetic Field Lines: The field lines created around a wire describe the direction of magnetic influence.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of two parallel wires carrying the same current attracting each other, demonstrating practical application in electromagnets.
-
Example calculation of the force between two conductors using Ampere's Law.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Parallel currents attract, opposite ones repel, a magnet's magic cast in a spell.
π Fascinating Stories
-
Two friends (currents) pulling together when side-by-side but pushing when they face apart, just like magnets going along in their parts.
π§ Other Memory Gems
-
Forces create paths: Alike attract, opposed distract.
π― Super Acronyms
FAP - For Attraction, Parallel; FIR - For Interaction, Reversals.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Ampere's Law
Definition:
A fundamental law describing the magnetic force generated around a conductor carrying current.
-
Term: Magnetic Field
Definition:
A field around a magnetic material or moving electric charge within which the force of magnetism acts.
-
Term: Force per Unit Length
Definition:
The force experienced by a conductor carrying current per unit length due to another conductor.
-
Term: RightHand Rule
Definition:
A mnemonic to determine the direction of the magnetic field created by current.
-
Term: Permeability of Free Space (\u03bc\u2080)
Definition:
A constant that describes how magnetic fields interact in a vacuum.