Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Solenoids
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will explore solenoids, which are essentially coils of wire. When current flows through them, they generate magnetic fields. Why do you think this might be useful?
Maybe for creating electromagnets?
Or in devices that need controlled magnetic fields?
Exactly! Solenoids have various applications, from electromechanical devices to scientific instruments. Now, letβs understand how they generate magnetic fields.
Deriving the Magnetic Field Inside a Solenoid
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
To find the magnetic field inside a solenoid, we can use Ampereβs circuital law. Can anyone tell me what that law states?
It relates the magnetic field around currents to the total current passing through a loop!
Great! So when we apply this law to a solenoid, we can derive that the magnetic field *B = ΞΌβnI*. How can we interpret this formula?
The *n* means the number of turns per unit length and does that mean more turns means a stronger field?
That's right! The more turns per unit length, the stronger the magnetic field. Letβs break down the significance of ΞΌβ and how it relates to the magnetic field strength.
Characteristics of Magnetic Fields Outside the Solenoid
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
What do you think happens to the magnetic field outside a long solenoid compared to inside it?
I think itβs weaker or maybe even zero?
Yeah, itβs like it doesnβt leak any field outside?
Exactly! The external field becomes negligible, especially as we increase the length of the solenoid, making it appear like a metal sheet. Now, letβs look at a quick example calculation.
Example Problem and Application
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Consider a solenoid with 500 turns and a current of 5 A. If it's 0.5 m long, how would we calculate the magnetic field inside it?
First, we calculate n, which is the total turns divided by the length, so n = 500/0.5.
Then we plug it into the formula B = ΞΌβnI and calculate the field!
Perfect! And this is how we can use solenoids for practical applications like electromagnets. Any questions left on solenoids?
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses the characteristics of a long solenoid, its properties in generating uniform magnetic fields, and applies Ampereβs law to derive the formula for the magnetic field inside it. Additionally, it illustrates the behavior of the magnetic field outside the solenoid and introduces examples to solidify understanding.
Detailed
Detailed Summary
In this section, we focus on the concept of a solenoid, which is essentially a long wire wound into a coil that produces a uniform magnetic field when an electric current flows through it. We define a long solenoid as one whose length is substantially greater than its radius, allowing for simplifications in analysis.
The magnetic field inside the solenoid can be derived using Ampere's circuital law, which states:
BL = ΞΌβI, where L is the length of the solenoid, ΞΌβ is the permeability of free space, and I is the current flowing through the solenoid.
From this relation, we can express the magnetic field B inside the solenoid as:
B = ΞΌβnI, where n is the number of turns per unit length of the solenoid.
The behavior of the magnetic field outside of the solenoid is characterized by a very weak or negligible field, which approaches zero as the solenoid becomes longer. This property makes solenoids particularly useful in applications needing uniform magnetic fields, such as electromagnets and inductors.
To further cement this understanding, examples illustrating the calculations of the magnetic field inside a solenoid and its applications are provided.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Solenoids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We shall discuss a long solenoid. By long solenoid we mean that the solenoidβs length is large compared to its radius. It consists of a long wire wound in the form of a helix where the neighbouring turns are closely spaced. So each turn can be regarded as a circular loop. The net magnetic field is the vector sum of the fields due to all the turns. Enamelled wires are used for winding so that turns are insulated from each other.
Detailed Explanation
A solenoid is essentially a coil of wire designed to create a magnetic field when an electric current passes through it. When we refer to a 'long solenoid,' we compare its length to its radius. In a long solenoid, this ratio is significant; thus, the magnetic field it produces can be considered uniform inside it. The wire is wound in a helical shape, and since each turn of wire contributes to the magnetic field, all these contributions need to be summed together. The use of enamelled wires ensures that the wire loops do not short-circuit each other, allowing the solenoid to function effectively.
Examples & Analogies
Think of a solenoid like a tightly wound spring; each coil of the spring is like a loop of wire. When you pass electricity through this 'spring,' it behaves like a magnet, similar to how wrapping a rubber band around a pencil makes it tighter. This concept is applied in many devices, such as electric door locks and MRI machines.
Magnetic Field in Solenoids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
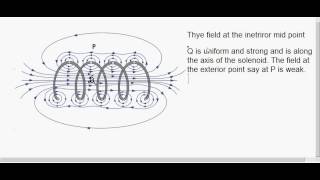
Figure 4.15 displays the magnetic field lines for a finite solenoid. We show a section of this solenoid in an enlarged manner in Fig. 4.15(a). Figure 4.15(b) shows the entire finite solenoid with its magnetic field. In Fig. 4.15(a), it is clear from the circular loops that the field between two neighbouring turns vanishes. In Fig. 4.15(b), we see that the field at the interior mid-point P is uniform, strong and along the axis of the solenoid. The field at the exterior mid-point Q is weak and moreover is along the axis of the solenoid with no perpendicular or normal component.
Detailed Explanation
The magnetic field lines inside a solenoid are parallel to each other and closely packed, indicating a strong and uniform magnetic field in that region. However, between each loop, the magnetic fields tend to cancel each other out, leading to a negligible field between the wires. Outside the solenoid, the magnetic field is much weaker and diminishes quickly as you move away from it. This pattern is crucial for applications needing focused magnetic fields, such as in electromagnets.
Examples & Analogies
Imagine turning on a flashlight. The beam of light is strong and focused when you press the button, similar to how the magnetic field in a solenoid is concentrated inside. However, once you shine that flashlight on a wall, the light spreads and weakens, much like how the magnetic field weakens as you move away from the solenoid.
Using Ampereβs Law for Solenoids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Consider a rectangular Amperian loop abcd. Along cd the field is zero as argued above. Along transverse sections bc and ad, the field component is zero. Thus, these two sections make no contribution. Let the field along ab be B. Thus, the relevant length of the Amperian loop is, L = h. Let n be the number of turns per unit length, then the total number of turns is nh. The enclosed current is, I = I (n h), where I is the current in the solenoid. From Ampereβs circuital law, BL = Β΅I , B h = Β΅I (n h) => B = Β΅nI.
Detailed Explanation
Using Ampereβs Law, we analyze how the current flowing through a solenoid results in a net magnetic field. The law states that the integral of the magnetic field along a closed loop is equal to the permeability of free space multiplied by the enclosed current. In a long solenoid, due to the uniform nature of the magnetic field in the core, we can conclude that the magnetic field inside a solenoid is proportional to the number of turns per unit length and the current flowing through it. The final equation shows how the magnetic field can be computed based on these factors.
Examples & Analogies
Imagine a traffic flow on a highway, where more lanes (similar to more turns in a solenoid) allow more cars (representing electrical current) to pass. The density of cars moving in the same direction (the crowd of cars) represents a stronger flow, which is analogous to the stronger magnetic field inside a solenoid. When we increase either the number of lanes or the speed limit, we see denser traffic, just like increasing the turns or current enhances the magnetic field.
Example of a Solenoid's Magnetic Field
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example 4.8 A solenoid of length 0.5 m has a radius of 1 cm and is made up of 500 turns. It carries a current of 5 A. What is the magnitude of the magnetic field inside the solenoid? Solution: The number of turns per unit length is, 500 / 0.5 = 1000 turns/m. B = Β΅nI = 4Ο Γ 10β7 Γ 1000 Γ 5 = 6.28 Γ 10β3 T.
Detailed Explanation
In this example, we calculate the magnetic field inside a solenoid by first determining the number of turns per unit length (n) and then applying the formula B = Β΅nI, where Β΅ is the permeability of free space. Plugging in the values from the problem gives us a specific strength of the magnetic field inside the solenoid, essential for understanding its behavior in practical applications.
Examples & Analogies
Think of the solenoid like a small, efficient factory assembly line. The more items (electric current) you put through the assembly line (the solenoidβs turns), the larger the output (magnetic field). Just like adding more workers would speed up production, increasing electric current or loops enhances the strength of the magnetic field.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Long Solenoid: A coil of wire producing a uniform magnetic field when current flows.
-
Ampere's Circuital Law: Used to derive the magnetic field inside the solenoid.
-
Magnetic Field Strength: Dependent on the number of turns per unit length and the current passing through the solenoid.
-
External Magnetic Field Behavior: The field outside the solenoid is negligible.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A solenoid with 500 turns carrying a current of 5 A produces a magnetic field calculated using B = ΞΌβnI.
-
Ampere's law allows us to derive the relationship between current, turns, and the resultant magnetic field.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
In a solenoid tight and round, a magnetic field can be found.
π Fascinating Stories
-
Imagine a coil wrapped neatly around a core, every time a switch flips, it opens the magic door creating fields that can lift and pullβsuch is the solenoid's rule.
π§ Other Memory Gems
-
S.O.L.E.N.O.I.D: Strong Organized Loops Engage Neatly On Inducing Direction (field lines)!
π― Super Acronyms
S=Solenoid, O=Organizes, L=Loops, E=Easily, N=Neatly, O=Outside, I=Induces, D=Direction.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Solenoid
Definition:
A coil of wire designed to create a magnetic field when an electric current passes through it.
-
Term: Ampereβs Law
Definition:
A law that relates the magnetic field around an electrical conductor to the electric current flowing through it.
-
Term: Magnetic Field (B)
Definition:
A vector field that represents the magnetic influence on moving electric charges, electric currents, and magnetic materials.
-
Term: Permeability (ΞΌβ)
Definition:
A physical constant that indicates how easily a magnetic field can penetrate a material.
-
Term: Turns per unit length (n)
Definition:
The number of complete coils of wire per unit length of the solenoid.