Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to CMOS XOR Gate
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're diving into the CMOS XOR gate. Does anyone know what an XOR gate does?
Isn't it a gate that gives a high output when inputs are different?
Exactly! The XOR gate outputs a high value when the inputs differ. Can someone give me an example of input combinations?
How about 0 and 1? That gives us an output of 1.
Right! And what about the case when both inputs are the same?
If both are 0 or both are 1, the output will be 0.
Perfect! Remember, this behavior is crucial for many digital applications. Letβs keep that in mind!
XOR Truth Table
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs analyze the truth table for the CMOS XOR gate. Can anyone summarize how itβs structured?
It shows all combinations of two inputs, A and B, and the resulting output!
Exactly! Hereβs what it looks like: when both inputs are 0, the output is 0; when they are different, the output is 1! Let's visualize it.
So, just to be sure, when A and B are both 1, the output is also 0?
Correct! Itβs like the gate is saying, 'I only care about different inputs!' Keep this table in mind as it has many applications in real-world circuits!
Applications of the XOR Gate
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs discuss the applications of the CMOS XOR gate. Any thoughts?
I think it's used in arithmetic operations, right?
Absolutely! The XOR gate is essential for binary addition. It helps in determining whether there's a carry or not. Any other applications?
I heard itβs also used for parity checks in error detection.
Great point! The exclusivity of the XOR gate makes it ideal for checking parity. It can help ensure data integrity. Fantastic connections to real-world systems!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The truth table for the CMOS XOR gate reveals its operational characteristics, where the output is high only when the inputs differ. A detailed exploration of this truth table is essential for understanding its role in digital logic.
Detailed
Detailed Summary of CMOS XOR Gate Truth Table
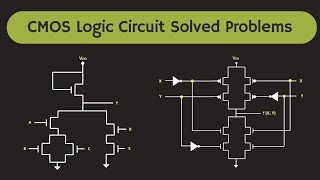
The CMOS XOR gate, or Exclusive OR gate, is a vital component in digital circuits utilized for various applications, including arithmetic operations and parity checks. The essence of an XOR gate lies in its ability to produce a high output (
1
) when an odd number of its inputs are high. In this case, with two inputs, the output will be high only when one input is high (1) while the other is low (0).
Truth Table of the CMOS XOR Gate
The truth table for a CMOS XOR gate can be defined as follows:
| Input A | Input B | Output (Vout) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Key Points:
- Output Characteristics: The output is high (1) for inputs that differ (0,1) or (1,0), showing the exclusive nature of the gate.
- Significance: XOR gates are crucial in digital systems where operations require differentiation between states, such as in arithmetic functions like addition.
Understanding this truth table is fundamental in analyzing the performance and application of CMOS technology in digital logic design.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Input Combinations for the XOR Gate
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
| Input | Input | Output |
|---|---|---|
| A | B | Vout |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Detailed Explanation
This table represents the behavior of the XOR gate. The XOR gate has two inputs, A and B, and produces an output Vout based on the values of these inputs. The table shows all the possible combinations of A and B and the corresponding output:
- When both inputs A and B are 0, the output Vout is also 0.
- When A is 0 and B is 1, Vout becomes 1.
- When A is 1 and B is 0, Vout is again 1.
- When both inputs are 1, the output Vout returns to 0.
Examples & Analogies
Think of the XOR gate like a light switch controlled by two different people. If they both want the light off (both are 0), the light is off (0). If only one person turns their switch on (one is 1 and the other is 0), the light turns on (1). But if both decide to turn it on (both are 1), the light is off (0) again. This scenario shows how XOR outputs high (1) only when the inputs are different.
Behavior of the XOR Gate
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The output of the XOR gate behaves as follows:
- It produces a high output (1) when an odd number of inputs are high.
- It produces a low output (0) when the inputs are the same.
Detailed Explanation
The XOR gate is unique because it outputs a high signal only when the inputs differ. In simpler terms:
- If one input is high (1) and the other is low (0), the output is high (1).
- If both inputs are the same (both high or both low), the output is low (0). This characteristic makes the XOR gate very useful in digital circuits, particularly in operations like error detection and odd parity checking.
Examples & Analogies
Imagine a voting system where two friends can vote for pizza toppings. If one votes for pineapple and the other for pepperoni, they agree on a topping (output is high). But if both vote for pineapple or both vote for pepperoni, they cannot agree on a unique topping (output is low). This reflects how the XOR gate operates with its inputs.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
XOR Gate: Outputs high when one input is high, and the other is low.
-
Truth Table: Represents all possible inputs and the corresponding outputs for a logic gate.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example: With inputs A=1 and B=0, the output of the XOR gate is 1, illustrating the gate's exclusivity.
-
Example: In a parity check, an XOR gate compares bits and determines if the number of ones in the input is odd.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
XOR is quite a clever gate, it only likes to differentiate.
π Fascinating Stories
-
Think of two friends at a party. If one is dancing and the other is not, they're having fun; if both stay still or both dance, it's a quiet night.
π§ Other Memory Gems
-
For XOR, think 'Odd one out': it turns on for the odd combination.
π― Super Acronyms
XOR
- 'Xcept One's Right' signifies the exclusivity of the gate.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: CMOS
Definition:
Complementary Metal-Oxide-Semiconductor, a technology for constructing integrated circuits.
-
Term: XOR Gate
Definition:
A digital logic gate that outputs true or high only when an odd number of inputs are true.
-
Term: Truth Table
Definition:
A mathematical table used to represent the output of a logic gate for all possible input combinations.