Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Valves and Flow Control
Unlock Audio Lesson
Today, we're exploring how valves can control fluid flow in a system. Can anyone tell me why valves are crucial in engineering?
They help stop or regulate the flow of fluids.
Exactly! Valves like gate and globe valves can significantly impact flow dynamics. For example, when a gate valve is fully closed, what happens to the flow?
The flow gets completely stopped.
Right! And if it’s only half open? What happens to the streamlines?
The flow might not be smooth, and there can be more turbulence and energy loss.
Correct! Remember: turbulent flow involves more energy loss due to friction. We can use the acronym **V.E.L.O.C.I.T.Y** to remember: *V*alves, *E*nergy, *L*oss, *O*bservation, *C*ontrol, *I*nteraction, *T*urbulence, *Y*ielding flows. Let’s summarize what we learned.
"1. Valves regulate flow, and different configurations lead to different flow characteristics.
Applying Linear Momentum Equations
Unlock Audio Lesson
Now, let's shift our focus to linear momentum equations. What do you think is meant by a control volume in fluid mechanics?
It's a specific volume within which we analyze fluid flow and forces.
Exactly! When applying linear momentum equations, we consider forces and pressure changes. What happens to shear stress in some cases?
We can often neglect it because it's much smaller than pressure forces.
Good! Remember the equation we derive from momentum flux and pressure force difference. Can anyone summarize the relationship?
The rate of change of momentum flux equals the pressure force difference!
Perfect! To reinforce this, we'll use the mnemonic **M.O.M.E.N.T**: *M*omentum, *O*utflow, *M*ass, *E*quation, *N*eglect, *T*hrough volume. Now, can someone recap why this is essential in engineering?
It helps us predict how fluids behave under different conditions!
Energy Loss through Bernoulli’s Equation
Unlock Audio Lesson
Let’s discuss Bernoulli’s equation, especially how we modify it to include head losses. What factors contribute to energy loss?
Friction and fittings, like valves or elbows.
Correct! When we apply modified Bernoulli’s equation, we can calculate these losses. What format does this equation take?
It equates the energy at one section to the energy at another, minus the losses.
Very good! Remember the formula: pressure head plus velocity head should equal the other section's equivalent, minus losses. We can use the acronym **H.E.A.D**: *H*ead, *E*nvironment, *A*nalysis, *D*ifferentials to remember this. Finally, summarize today's key concepts.
"1. Modified Bernoulli’s equation quantifies energy losses.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section outlines how to apply linear momentum equations along with mass conservation principles to analyze fluid flow. It explores different valve types and how they impact flow dynamics, including vortex formation and energy losses in pipe systems.
Detailed
Application of Linear Momentum Equations
In this section, we delve into the application of linear momentum equations essential for solving fluid flow problems involving valves and pipes. The foundational understanding lies in recognizing that solving a majority of flow-related issues hinges on the application of mass conservation and momentum principles.
Key Points:
- Valves and Flow Control: The discussion includes different types of valves, such as gate and globe valves, and how their configurations affect fluid dynamics. The valve's position influences flow rates, leading to varying pressure distributions and energy losses.
- Streamline Behavior: The movement of streamlines and the behavior of vortices in fluid flow are analyzed, especially under conditions such as fully closed, half-open, and fully open valves. Each position affects energy dissipation differently.
- Control Volume Analysis: The concept of control volumes is introduced, with a focus on applying linear momentum equations to analyze forces acting within these volumes. The shear stress component may be neglected under certain conditions, simplifying calculations.
- Bernoulli’s Equation: The modified Bernoulli equation is presented, incorporating head loss due to friction and fittings, providing a quantitative approach to analyzing energy changes between different sections of a pipeline.
- Calculating Energy Losses: The section details methods to compute energy loss through various components like elbows and tees, emphasizing the need for understanding K-factors for different geometries.
This comprehensive overview of applying momentum equations illustrates their significant role in fluid mechanics, integral to engineering applications, particularly in designing and analyzing piping systems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Control Volume and Flow Regulation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look it that most of the times also we have a valve to control the flow okay which is a gate valve okay, it is a gate type of systems. If you rotate it this valve closes the waters okay. And it can have a total open or half closed and all these conditions to regulate the flow to regulate the flow we have a these systems. Now if you look it if I am to draw the streamlines, how it happens it.
Detailed Explanation
In fluid dynamics, controlling flow is essential. A gate valve is a common tool used to manage the flow of fluids in a pipeline. By opening or closing this valve, we can regulate how much fluid passes through. When the valve is completely open, maximum fluid flow occurs. However, if it is partially opened, the flow becomes turbulent, which can complicate the flow patterns. Drawing the streamlines gives a visual representation of how fluid flows around obstacles, which is crucial for understanding fluid movement.
Examples & Analogies
Think of the gate valve like a faucet. When you open the faucet fully, water rushes out quickly, similar to a fully open valve. If you turn the faucet just halfway, the water flow slows down, causing changes in how the water spouts and splashes. This change in flow helps us understand how valves influence pipeline systems.
Valve Types and Energy Losses
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look it similar way we have a the globe valve which is more control valve systems. The flow comes here, then rotate it and this valve it goes off and flow goes like this. So we can look it now in terms of vortex formations here, the vortex formations here, and once flow goes it also could have the vortex formations also here.
Detailed Explanation
A globe valve functions as a more intricate control mechanism compared to a gate valve. As the globe valve is adjusted, it modifies how the fluid flows, potentially causing vortex formations. These vortices indicate turbulent flow patterns, which can lead to energy losses within the system. Understanding the differences between valve types allows engineers to select the appropriate valve based on specific applications and the required control over fluid motion.
Examples & Analogies
Imagine running your hand through water; the way your hand swirls the water mimics how vortex formations occur in fluid systems. If your hand (representing a valve) is moved or rotated, it changes the flow, creating eddies or swirls that demonstrate how vortices can form, leading to energy losses in pipelines.
Applying Linear Momentum Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
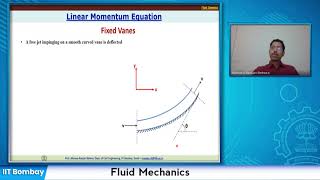
Now coming to this, I am just applying the linear momentum equations for these control volumes okay. So if you have this is the control volumes. So you may have the shear stress is acting on this okay, this the shear stress part, okay. But we are neglecting this part, we are neglecting the shear stress part.
Detailed Explanation
Linear momentum equations help in calculating the forces that act upon a control volume in a fluid system, focusing primarily on pressure differences rather than shear stresses. As the shear stress is usually negligible in such equations, the task becomes simpler by equating pressure force differences with momentum fluxes. This simplification makes it easier to analyze and predict how fluids behave under various configurations and conditions.
Examples & Analogies
Think of pushing a swing; your push relates to your momentum, which affects how high the swing goes. Similarly, linear momentum equations relate the forces acting on a control volume to how the fluid moves within that volume, making management of fluid systems (like swings in motion) easier.
Bernoulli's Equation Application
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now I will applying Bernoulli’s equations along the straight line, okay I am just applying the Bernoulli’s equation along the straight line. When you apply the Bernoulli’s equations, this line is horizontal. This streamline is horizontal, so you do not have a z components.
Detailed Explanation
Bernoulli's equation relates pressure, velocity, and height in fluid flows. When we apply it along a streamline, particularly in horizontal flows, we focus only on pressure and velocity head, ignoring elevation changes. Understanding how energy losses are quantified in this manner aids engineers in evaluating flow efficiency and predicting pressure variations throughout a system.
Examples & Analogies
Imagine a water slide: when a person goes down, they may speed up (increasing velocity) while losing potential height. Keeping track of the speed and pressure felt at different points relates to how we use Bernoulli’s equations to evaluate the energy and behavior of fluid flow.
Energy Loss Calculations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is what we have derived lot. So this is a rate of change of the momentum flux is equal to the, the pressure difference between the, the pressure force difference between this p and p and that what if you rearrange it you will get it this part okay.
Detailed Explanation
Calculating energy losses in a fluid system requires understanding how momentum flux changes with pressure differences. By rearranging equations concerning pressure and momentum flux, engineers can derive essential relationships that help predict how energy dissipates through valves and fittings in a system, which is critical for effective design and efficiency.
Examples & Analogies
Think of the energy loss while pouring syrup onto pancakes. The pressure you exert to pour the syrup will determine how fast and how far it goes—similar to how changes in pressure affect fluid flow through pipelines and the accompanying energy losses.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Momentum: The product of mass and velocity critical to the movement of fluids.
-
Streamlines: Path lines that fluid particles follow, crucial for analyzing flow behavior.
-
Bernoulli's Equation: Fundamental equation in fluid dynamics that relates pressure, velocity, and elevation.
-
Control Volume: A system boundary through which mass and energy conservation laws are applied.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of using Bernoulli's equation to calculate pressure differences at two points in a pipe system.
-
Illustration of how different valve types affect energy losses in fluid flow.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluid flow, momentum's key, keeps the liquid moving free.
📖 Fascinating Stories
-
Imagine a river with various gates controlling how much flows; each valve influences the current and energy loss.
🧠 Other Memory Gems
-
Use the mnemonic M.O.M.E.N.T to remember the flow control principles.
🎯 Super Acronyms
H.E.A.D helps recall Bernoulli's modifications
- Energy calculations that head through losses.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Momentum
Definition:
A physical quantity defined as the product of mass and velocity.
-
Term: Streamlines
Definition:
Imaginary lines that indicate the flow direction of fluid particles.
-
Term: Bernoulli's Equation
Definition:
An equation that describes the conservation of energy in fluid dynamics.
-
Term: Control Volume
Definition:
A defined region in space across which mass and momentum balances are applied.
-
Term: Valves
Definition:
Devices that regulate the flow of fluids in a system.
-
Term: Energy Loss
Definition:
The dissipation of energy, often resulting from friction and turbulence in fluid flow.