Gradual and Sudden Contractions
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Flow Types and Their Impacts
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will explore how different flow types, like laminar and turbulent, affect energy in fluid systems. Can anyone tell me what laminar flow is?

I think laminar flow is smooth and orderly, with layers of fluid sliding past each other.

Exactly! And what about turbulent flow?

Turbulent flow is chaotic, with mixing and fluctuations in speed.

Correct! Remember, laminar flow has less energy loss compared to turbulent flow. We can remember this with the mnemonic 'L for Less loss.'
Understanding Valves and Flow Regulation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Moving on, let's discuss gate valves and globe valves. Who can explain how a gate valve operates?

A gate valve either completely opens or closes the flow.

Exactly! And what about globe valves? How do they differ?

Globe valves control the flow more precisely since you can adjust them partially.

Great job! They can lead to more energy loss if not used correctly. A simple rhyme could help: 'Gate for great flow, Globe slows down the go!'
Application of Bernoulli’s Principle
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's relate our discussion to Bernoulli’s equation. How can we express energy losses in fluid systems?

We can use modified Bernoulli’s equation to account for head losses.

That's right! The equation helps visualize the energy change from one section of flow to another due to friction losses. Can someone memorize the modified equation for energy losses?

Sure! It's like saying: Energy in = Energy out - Energy loss!

Excellent summary! Remember the acronym: 'E = E - L' for easier recall.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section explores flow characteristics through various types of valves and the resulting changes in energy distributions and momentum. It explains how to apply mass conservation and linear momentum equations to model the flow process accurately.
Detailed
Detailed Summary
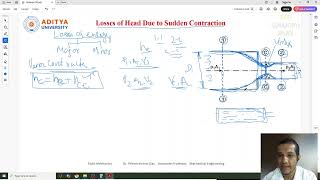
In this section, we delve into the effects of gradual and sudden contractions in fluid dynamics, particularly focusing on their implications for energy losses and pressure distributions. The discussion begins by highlighting the importance of understanding flow control mechanisms, such as gate and globe valves, which regulate flow rates and can induce vortex formations that impact energy losses. The section emphasizes the strategic application of mass conservation, linear momentum, and Bernoulli’s equations to analyze flow behaviors.
Key concepts include:
1. Streamline Patterns: The arrangement of flow lines around valves varies based on their opening positions, leading to different vortex formations.
2. Energy Losses: It is noted that energy losses differ substantially between gradual and sudden contractions in pipes, and the equations governing these losses are derived.
3. Flow Types: The section distinguishes between laminar and turbulent flows, explaining how their characteristics affect velocity distributions and resultant energy losses. The use of control volumes allows for a systematic approach in applying conservation principles for incompressible flows. Finally, the section introduces a modified Bernoulli’s equation to account for energy losses in both gradual and sudden contractions, clarifying how these losses can be measured through parameters associated with the type of valve and flow conditions.
This understanding is crucial for students as it lays the foundation for effective fluid system designs and the application of hydraulics in engineering.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Flow Control with Valves
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If you look it that most of the times also we have a valve to control the flow okay which is a gate valve okay, it is a gate type of systems. If you rotate it this valve closes the waters okay. And it can have a total open or half closed and all these conditions to regulate the flow to regulate the flow we have a these systems.
Detailed Explanation
In fluid systems, valves are crucial components used to manage the flow of fluids. A gate valve, for example, can either be fully open, partially open, or fully closed. When fully open, the valve allows maximum flow. If closed, it stops the flow completely. In its half-open condition, it regulates the flow, which can create complex flow patterns downstream, including changes in pressure and velocity. Understanding how these valves work is essential to effectively control fluid systems in various applications.
Examples & Analogies
Imagine a garden hose with a nozzle. When you turn the nozzle to fully open, water gushes out. If you turn it halfway, the flow is reduced to a trickle, which illustrates how a valve regulates flow. Just like with the nozzle, adjusting the valve in a fluid system can significantly change the flow characteristics and behavior.
Streamline Patterns with Valve Adjustments
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now if you look it if I am to draw the streamlines, how it happens it. So streamlines will come like this okay. There could be the vortex formations. And if you try to understand it, that I have not this open or the totally close, if the half open your flow distributions you can understand it how the streamlines patterns will come, how the vortex formations will have.
Detailed Explanation
Streamlines represent the path that fluid particles follow in a flow. Depending on the position of the valve (open, half open, or closed), these streamlines will change. In a fully closed valve, no fluid passes, while an open valve allows for a straight flow, producing distinct streamlines. When the valve is half open, it can cause changes in pressure, leading to vortex formations. These vortices are swirling actions of the fluid that occur when flow turns or changes direction sharply. Understanding these behaviors is crucial for effective fluid management in engineering systems.
Examples & Analogies
Think of a river with a bend. When the water flows straight, the current is directed and smooth (like an open valve). However, if there’s an obstacle or if the river narrows, the water may swirl around it and create eddies (similar to vortex formations when the valve is half open). This visualization helps to understand how obstacles and openings affect fluid dynamics.
Energy Losses in Valves
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If you look it that way and just compare to valves one is globe valve and the gate valve this require for different type of discharge conditions. So if you look at these conditions you can easily interpret it we will have a more energy losses for this case as compared to this ones.
Detailed Explanation
Different types of valves, like gate valves and globe valves, have different energy characteristics. For instance, globe valves generally cause more energy loss than gate valves due to their design and how they restrict flow. This restriction leads to turbulence and energy dissipation as fluid passes through. In hydraulic systems, it is crucial to select the right type of valve to minimize energy losses and optimize performance.
Examples & Analogies
Think of driving a car on a road with different surfaces. Driving on a smooth highway (like a gate valve) feels easier and maintains speed better compared to driving over a rough, bumpy road (like a globe valve), where you constantly slow down. Similarly, the design of valves affects how smoothly fluid can flow through a system.
Deriving Energy Losses and Pressure Distributions
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let us come for derivations of energy losses and the pressure and velocity distributions of having a systems where two pipes we are enlarging it from the smaller diameter to bigger diameters. If you have that conditions and you can draw the velocity distributions. The velocity distribution it depends upon the type of the flow. If I have a laminar flow, the velocity distribution is different. If I have a turbulent flow velocity distributions is different.
Detailed Explanation
When fluids move through pipes, especially when transitioning from a smaller diameter to a larger one, the velocity distribution is affected by the type of flow—laminar or turbulent. In laminar flow, fluid moves in parallel layers with minimal disruption, resulting in a smooth velocity profile. Conversely, turbulent flow is characterized by chaotic movements and mixing, leading to a more complex velocity profile. Knowing how these different types of flow affect velocity is vital for predicting performance in fluid systems.
Examples & Analogies
Imagine pouring syrup into a wide bowl versus a narrow slot. In the narrow slot (laminar flow), the syrup flows smoothly in one direction. In the wide bowl (turbulent flow), the syrup swirls around and mixes, illustrating how changes in pipe diameter can lead to different flow behaviors in fluid systems.
Applying Bernoulli’s Equation
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now I will applying Bernoulli’s equations along the straight line, okay I am just applying the Bernoulli’s equation along the straight line. When you apply the Bernoulli’s equations, this line is horizontal. This streamline is horizontal, so you do not have a z components. You have pressure head component and the velocity head component.
Detailed Explanation
Bernoulli's equation is a fundamental principle in fluid dynamics that relates pressure, velocity, and height in a flowing fluid. When applying this equation along a streamline that remains parallel to the ground, we can ignore potential energy due to height differences. Thus, we focus on pressure and velocity heads. This simplification allows engineers to calculate how changes in velocity affect fluid pressure at different points in a system, illustrating the trade-off between these two energy forms.
Examples & Analogies
Consider a garden hose with water flowing through. As you partially cover the end of the hose with your thumb (reducing the cross-sectional area), the water speeds up (increased velocity), causing a drop in pressure at that point (it may spray out further). This scenario demonstrates how Bernoulli’s principles apply in everyday fluid movement.
Key Concepts
-
Mass Conservation: Keeps fluid mass constant across flow sections.
-
Momentum: Describes how motion is transferred through momentum flux.
-
Energy Losses: Result from friction in flow control devices like valves.
Examples & Applications
Example of gradual contraction: A pipe narrowing from a diameter of 4 inches to 2 inches will experience gradual changes in velocity and pressure.
Example of sudden contraction: A sudden change in the pipe diameter from 4 inches to 1 inch can lead to an abrupt drop in pressure and increased energy loss.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In smooth laminar flow, the layers glide, while turbulent chaos likes to hide.
Stories
Imagine a river flowing peacefully: that's laminar. Now picture a storm causing whirlpools: that's turbulent.
Memory Tools
For Bernoulli: Energy = Pressure + Velocity + Height (E = P + V + H).
Acronyms
G.E.A.R for Gate Valve
for Great flow control
for Efficient
for All or nothing
for Regulated.
Flash Cards
Glossary
- Laminar Flow
A smooth, orderly flow characterized by layers of fluid moving parallel to each other.
- Turbulent Flow
A chaotic flow pattern characterized by mixing and fluctuations in fluid velocity.
- Bernoulli’s Equation
An equation that relates the pressure, velocity, and height in a flowing fluid, allowing for calculation of energy losses.
- Control Volume
A specified region in fluid mechanics where mass and energy balances are applied.
- Gate Valve
A valve that fully opens or closes fluid flow without adjustment.
- Globe Valve
A valve that regulates fluid flow precisely through partial opening.
Reference links
Supplementary resources to enhance your learning experience.
