Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Bernoulli's Equations
Unlock Audio Lesson
Today, we're diving into Bernoulli's equations, which play a crucial role in fluid dynamics. Can anyone tell me what Bernoulli's principle states?
Is it about the relationship between pressure and velocity in a fluid?
Excellent! Bernoulli's principle states that for an incompressible, non-viscous fluid in a steady flow, the total mechanical energy along a streamline is constant. We can remember this with the acronym 'PE + KE = TE', where PE stands for pressure energy, KE for kinetic energy, and TE for total energy.
So, how does this apply in real-world scenarios?
Good question! Bernoulli’s equation can help us analyze systems like pipelines or airfoils to predict how flow will change with different pressures and velocities.
Application of Bernoulli’s Equation with Valves
Unlock Audio Lesson
Now let’s shift our focus to how flow control devices, such as valves, utilize Bernoulli's principles. Can anyone name a type of valve and describe how it might affect flow?
A gate valve can control the flow by completely opening or closing, right?
Exactly! However, when partially opened, it can create turbulence and energy losses. Remember the term 'minor losses' that we classify based on these conditions.
What about globe valves?
Great point! Globe valves offer better control over flow than gate valves but generally incur higher energy losses due to their design.
Energy Losses and Flow Characteristics
Unlock Audio Lesson
Let's discuss energy losses in fluid flow. What are the two primary types of flow characterized by energy distribution?
Laminar and turbulent flow!
Correct! Laminar flow has smooth and orderly lines, while turbulent flow is chaotic. The energy losses are impacted considerably by these flow characteristics.
How do we quantify these losses?
We quantify energy losses using head loss coefficients related to valves and fittings, and we calculate them using Bernoulli's modified equations.
Hydraulic and Energy Gradient Lines
Unlock Audio Lesson
Finally, let’s visualize the effects of energy losses using energy gradient lines. Who can explain the difference between energy gradient and hydraulic gradient lines?
The energy gradient line shows the total energy per unit weight of fluid, while the hydraulic gradient only shows the energy due to pressure.
Exactly! The hydraulic gradient line typically lies below the energy gradient line, assuming there are energy losses due to friction.
Can these lines help us design better fluid systems?
Yes! Understanding these lines can greatly improve the effectiveness of piping systems. The better you visualize energy losses, the more efficient your designs will be.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section dives into the principles of Bernoulli's equations along with the concepts of mass conservation and linear momentum. It highlights how these principles can be applied to control flow through devices such as valves and explores energy losses in various flow scenarios, including laminar and turbulent flows.
Detailed
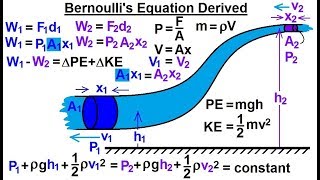
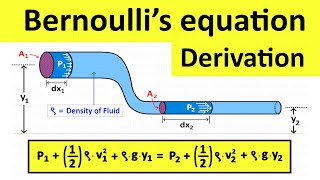
Bernoulli's Equations
The section provides an extensive overview of Bernoulli's equations and their significant role in fluid dynamics. It starts by emphasizing the critical need to master concepts like mass conservation equations and linear momentum equations to effectively utilize Bernoulli’s equations.
The discussion transitions to practical applications involving flow control valves, such as gate and globe valves, elucidating how they affect flow characteristics and energy losses. The section elaborates on the conditions for flow distributions, including laminar and turbulent flows that dictate different velocity distributions.
Further, by applying linear momentum equations to control volumes, the section outlines the derivation of energy losses due to pressure and velocity distributions across varying pipe diameters and flow conditions. The modified Bernoulli's equation is presented, which incorporates energy losses during flow and solidifies the foundational connection between pressure, velocity, and energy in fluid systems.
Finally, the section addresses various methods of calculating energy losses, introduces head loss coefficients, and touches on the graphical interpretation of hydraulic and energy gradient lines, all essential for designing efficient hydraulic systems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Bernoulli's Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you try to understand that or try to draw that sketch you solve the 20% of the problems, another 20 I can say not the 20% maybe 50% of problems. Another 50% is that how to apply mass conservations equations, linear momentum equations and the Bernoulli’s equations which it is not that difficult to apply it. So the basically the strategy is that you should try to understand these ones.
Detailed Explanation
This section emphasizes the importance of understanding Bernoulli's equations along with mass and momentum conservation equations as a key strategy in solving related problems. By grasping these principles, a significant proportion of the challenges encountered can be tackled effectively.
Examples & Analogies
Think of Bernoulli's equation as a toolbox. When you learn how to use it alongside other tools like mass conservation, it simplifies complex problems in fluid dynamics, just like knowing how to assemble a furniture piece becomes easier when you understand how all the tools fit together.
Flow Control Using Valves
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look it that most of the times also we have a valve to control the flow okay which is a gate valve okay, it is a gate type of systems. If you rotate it this valve closes the waters okay. And it can have a total open or half closed and all these conditions to regulate the flow to regulate the flow we have a these systems.
Detailed Explanation
This chunk describes the use of valves, particularly gate valves, to control water flow. By adjusting the position of a valve (fully open, half-closed, etc.), the flow can be regulated effectively. Understanding how these devices alter flow dynamics is crucial in applying Bernoulli's principles.
Examples & Analogies
Imagine you're watering a garden with a hose that has a nozzle. When you twist the nozzle to open it wide, a strong stream of water flows out. When you partially close it, the flow decreases, and the direction of water changes, similar to how valves control the flow in plumbing systems.
Streamlines and Flow Patterns
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look it similar way we have a the globe valve which is more control valve systems. The flow comes here, then rotate it and this valve it goes off and flow goes like this. So we can look it now in terms of vortex formations here, the vortex formations here, and once flow goes it also could have the vortex formations also here.
Detailed Explanation
This section transitions to discussing globe valves and their role in controlling flow. It emphasizes the significance of understanding streamlines and vortex formations which occur in fluid flow as it interacts with these valves. The way flow patterns change significantly impacts the energy loss in the system.
Examples & Analogies
Consider a river flowing around a rock. As water encounters the obstacle, it forms whirlpools or vortices. Similarly, when flow passes through a globe valve, it can create unexpected turbulence. Realizing this can help in designing systems that minimize energy losses.
Energy Loss in Pipe Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us come for derivations of energy losses and the pressure and velocity distributions of having a systems where two pipes we are enlarging it from the smaller diameter to bigger diameters.
Detailed Explanation
Here, the discussion shifts to analyzing energy losses as fluid moves through pipes of varying diameters. The concept is that as the pipe diameter increases, the velocity changes, impacting the system's pressure and energy. This is crucial in designing efficient fluid systems.
Examples & Analogies
Think of a funnel where a wide end lets liquid flow rapidly. In a narrow section, the liquid slows. Similarly, pipes with varying diameters experience similar behavior in fluid speed and energy loss. Understanding this helps in designing smoother flow systems.
Application of Linear Momentum Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if you have this control volumes. So you may have the shear stress is acting on this okay, this the shear stress part, okay. But we are neglecting this part, we are neglecting the shear stress part.
Detailed Explanation
This chunk focuses on the application of linear momentum equations within control volumes in fluid mechanics. It highlights the simplifying assumption of neglecting shear stress in favor of emphasizing pressure forces, which are more significant in most scenarios.
Examples & Analogies
Consider a boat floating on water. The push from the water (pressure) allows it to move more so than the tiny friction between the hull and water (shear stress). Just as you ignore minor forces when considering the boat's motion, engineers simplify fluid calculations by sometimes neglecting shear stress.
Applying Bernoulli’s Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
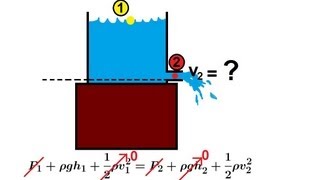
Now I will applying Bernoulli’s equations along the straight line, okay I am just applying the Bernoulli’s equation along the straight line. When you apply the Bernoulli’s equations, this line is horizontal.
Detailed Explanation
In this section, Bernoulli’s equation is applied to a horizontal streamline. The absence of potential energy (z component) simplifies calculations, allowing for a direct relationship between pressure head and velocity head, which quantifies energy losses.
Examples & Analogies
Imagine a slide at a playground. When a child slides down, their potential energy converts to speed (kinetic energy). Similarly, Bernoulli’s equation shows how energy transitions in flowing fluids, simplifying complex calculations like a straight-down slide lets you predict speed without friction.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Bernoulli's Principle: Describes the relationship between velocity and pressure in fluid flow.
-
Flow Control Devices: Explain how valves control flow and lead to energy losses.
-
Energy Losses: The impact of pipe diameter, flow type, and other factors on energy losses in systems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The use of a gate valve reduces the flow area, affecting pressure and velocity according to Bernoulli’s principle.
-
In a turbulent flow, energy losses can be significantly higher compared to laminar flow due to chaotic movement.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluid flows of varying speed, pressure falls where velocity's freed.
📖 Fascinating Stories
-
Imagine a river with turns; where it narrows, the water runs fast, creating whirlpools—a reminder of how flow resistance increases energy loss.
🧠 Other Memory Gems
-
PE + KE = TE helps you see, how pressure, velocity, and height agree!
🎯 Super Acronyms
Remember 'K' for 'K-factor', which shows losses in flow with a reactor.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Bernoulli’s Equation
Definition:
A formula that describes the conservation of energy in fluid flow, relating pressure, velocity, and height.
-
Term: Incompressible Flow
Definition:
A flow in which the fluid density remains constant.
-
Term: Mass Conservation
Definition:
Principle stating that mass cannot be created or destroyed in an isolated system.
-
Term: Minor Losses
Definition:
Energy losses due to fittings, valves, and other components in a flow system.
-
Term: Laminar Flow
Definition:
A type of flow characterized by smooth and orderly movement of fluid.
-
Term: Turbulent Flow
Definition:
A type of flow characterized by chaotic property changes, leading to energy losses.