Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Convolution
Unlock Audio Lesson
Today, we're going to start our session with convolution, a fundamental operation in system response theory. Convolution allows us to determine how the output of a system reacts to inputs over time. Can anyone tell me what they think convolution means?
Isn't convolution just combining two functions together somehow?
That's a good start! Convolution involves an integration process that combines two functions, usually to find the output of linear time-invariant systems. To make this clearer, imagine you have a signal and a system response. You want to see how that signal gets transformed by the system.
So, we are basically seeing how a function changes with a certain input?
Exactly! When we convolve a function with a delta function, the output should be the same as the input function. This brings us to the identity property of the delta function in convolution.
How does that work?
Great question! Mathematically, we represent this as $$f * δ = f(t)$$. It preserves the form of the function. Would anyone like to summarize what we just discussed?
Convolution combines functions, and using a delta function keeps the original function's shape intact.
Well done! Now, let's delve into applications of this property.
Practical Applications in Engineering
Unlock Audio Lesson
Now that we understand the basics, let's look at where this is used, especially in civil engineering applications.
Are we talking about how structures respond to loads?
Precisely! In structural vibration analysis, we need to know how structures react to different loadings over time. By using convolution with a delta function, we can effectively model and predict these responses.
What about control systems? How does this apply there?
In control systems, feedback is crucial. By utilizing convolution, we ensure that the system reacts appropriately to instantaneous inputs, maintaining stability and desired responses.
So, convolution helps us understand dynamic systems?
Exactly! That's key in analyzing the behavior of systems with varying conditions and in designing reliable systems. Let's do a quick recap.
Convolution helps analyze system responses and applies notably in structural and control systems.
Very good! Let's proceed to exercises to reinforce our understanding!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section details how convolution with the Dirac delta function acts as an identity operation for functions, preserving their shape. It discusses the mathematical implications of this property and its practical applications in fields like structural vibration analysis and real-time control systems.
Detailed
Convolution with the Delta Function
In this section, we explore the concept of convolution involving the Dirac delta function, denoted as δ(t). Convolution is a crucial operation in system response theory, particularly in signal processing and linear time-invariant (LTI) systems. The delta function serves as an identity element in convolution operations, which can be mathematically expressed as:
$$
(f * δ)(t) = \
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Convolution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Convolution is a key operation in system response theory.
Detailed Explanation
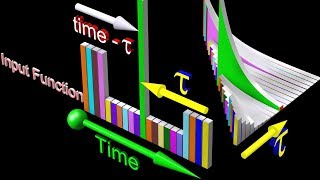
Convolution is a mathematical operation used to combine two functions. It describes how the shape of one function is modified by another. In system response theory, this helps us understand how a system reacts to various inputs over time. Specifically, we often deal with inputs (like forces or signals) and want to know how the system will respond to these inputs. The convolution operation allows us to calculate this response accurately.
Examples & Analogies
Imagine a sponge soaking up different colors of dye. The sponge represents the system, while the dye colors are the different inputs. The way the sponge changes color as it absorbs the dye can be thought of as convolution. Each color affects how the sponge looks after absorption, just like inputs affect system responses.
The Role of the Delta Function in Convolution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
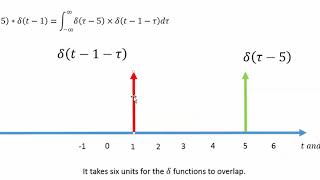
The delta function acts as an identity in convolution: Z ∞ (f ∗δ)(t)= f(τ)δ(t−τ)dτ =f(t) −∞
Detailed Explanation
In convolution, the Dirac delta function, denoted as δ(t), acts as an identity element. When you convolve any function f(t) with the delta function, the result is the function itself. This is due to the unique properties of the delta function, which effectively 'samples' the function at a certain point. The equation shows that when the delta function is involved in convolution, the output retrieves the value of the input function at the specific time of interest.
Examples & Analogies
Consider you have a light switch (the delta function) controlling a lamp (the function f(t)). When you flip the switch at a certain moment, the lamp lights up exactly at that moment, representing the value of f(t) at that time. Just like how the switch immediately affects the lamp, the delta function immediately retrieves the value of f(t).
Applications in Civil Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In civil engineering: • Convolution is used in structural vibration analysis, • To determine response functions to arbitrary loading, • To model real-time feedback in control systems.
Detailed Explanation
In civil engineering, convolution is crucial for analyzing how structures react to different loads and vibrations. For example, when a building is subjected to an earthquake, engineers can use convolution to predict how the building will respond over time, based on the initial forces applied. This is also essential in control systems that require continuous feedback adjusting to real-time changes in the environment.
Examples & Analogies
Think of a bridge that bounces up and down when cars drive over it. Engineers need to predict how much the bridge will sway (or vibrate) as cars pass. By using convolution, they can model these vibrations based on various traffic patterns, ensuring the bridge remains safe and functional, just like how a music conductor adapts their rhythm to match the tempo of the orchestra while ensuring the performance’s quality.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Convolution: A mathematical operation for combining two functions.
-
Delta Function: An idealized function that acts as an identity in convolution.
-
Linear Time-Invariant Systems: Systems that maintain constant behavior over time.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Modeling the response of a structural system to an impulsive load using convolution with the delta function.
-
Applying real-time feedback in control systems through convolution to enhance system stability.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In convolution, when we play, the delta keeps the shape at bay.
📖 Fascinating Stories
-
Imagine a friend throwing a ball (the function) at the wall (the delta function). The ball bounces right back, just like the original function after convolution.
🧠 Other Memory Gems
-
D for Delta, C for Convolution - Remember that convolution returns the original!
🎯 Super Acronyms
D.F.I. - Delta Function Identity - helps to remember that delta returns a function unchanged.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Convolution
Definition:
A mathematical operation that combines two functions to produce a third function, representing how the shape of one is modified by the other.
-
Term: Delta Function
Definition:
A generalized function that represents an idealized point mass or impulse; it acts as an identity element in convolution.
-
Term: Linear TimeInvariant System
Definition:
A system where the output is linearly responsive to input over time, and its behavior does not change with time.