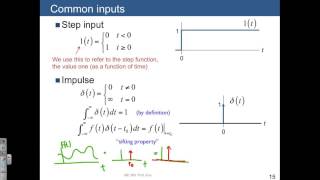
Sifting Property
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Sifting Property
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will explore the sifting property of the Dirac delta function. Can anyone tell me what they think this property does?

Is it related to how the delta function picks values from a function?

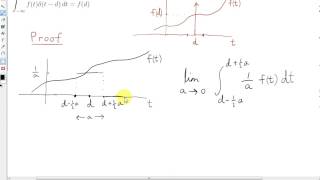
Exactly! The sifting property allows the delta function to 'sift' through a function and extract its value at a particular point. This is represented mathematically as \( \int_{-\infty}^{\infty} f(x) \delta(x - a) dx = f(a) \).

So, it basically means if I have a function and I multiply it by the delta function, I can find its value at a specific point?

That's correct! Think of the delta function as a filter that highlights one specific value, effectively simplifying complex calculations.
Applications of the Sifting Property
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's delve into how this property is used in civil engineering. Why do you think it's important in analyzing point loads?

Because point loads can affect structures at specific locations, right?

Exactly! When we apply a point load at a location, the sifting property allows us to determine how that load influences other areas of a structure, keeping our analyses accurate.

Can you give an example of where this would apply?

Sure! When analyzing a simply supported beam with a concentrated load, we can use the sifting property to simplify the governing differential equations, making it easier to calculate deflections.
Mathematical Breakdown of the Sifting Property
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s break down the integral. What happens to the value of the function f(x) when multiplied by the delta function?

It only matters where the delta function is non-zero, right?

Exactly. The delta function is zero everywhere except at x = a. Thus, the entire integral collapses to just f(a) since all other values contribute nothing.

So if f(x) were a complicated function, I could still just evaluate it at one point?

Precisely! The sifting property simplifies many calculations across engineering disciplines.
Visualizing the Sifting Property
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s visualize the sifting property. Imagine f(x) as a curve and δ(x-a) as a spike at point a. What would you visualize happening during integration?

The spike probably highlights the value of f(a) while the rest of the curve doesn't matter?

Exactly! The delta function only shines a light on f(a), and when we integrate, only that peak counts. This visualization is crucial for understanding how delta functions simplify real-world phenomena.

And that’s why we can model point loads so effectively in structures!

Right you are! Integrating with the delta function allows us to make precise and practical evaluations in engineering.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section elaborates on the sifting property of the Dirac delta function, which states that the integral of a function multiplied by the delta function at a shifted position equals the function's value at that position. This property is vital for evaluating impacts of point loads and other concentrated effects in civil engineering.
Detailed
Detailed Summary of the Sifting Property
The sifting property is one of the most important characteristics of the Dirac delta function, denoted as δ(x - a). This property is defined mathematically as:
\[ \int_{-\infty}^{\infty} f(x) \delta(x - a) dx = f(a) \]
This equation emphasizes that the integral of a function f(x) multiplied by a delta function centered at point a effectively 'sifts out' the value of the function at that point. In civil engineering, this property is particularly useful for analyzing systems subjected to point loads or impulses, allowing engineers to simplify the evaluation of loads and ensure accurate assessments of structural effects and responses. Thus, the sifting property enables effective assessments and solutions in structural analysis, facilitating the modeling of real-world applications.
Youtube Videos

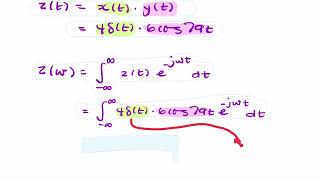




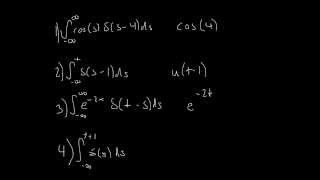

Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the Sifting Property
Chapter 1 of 1
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
One of the most important properties of the Dirac delta function is its sifting or sampling property:
\[ \int_{-\infty}^{\infty} f(x) \delta(x - a) dx = f(a) \]
This means \( \delta(x - a) \) “picks out” the value of \( f(x) \) at \( x = a \). This is useful in civil engineering when evaluating the effect of a point load or impulse at a specific location.
Detailed Explanation
The sifting property of the Dirac delta function states that when we integrate a function multiplied by the delta function, the result is simply the value of that function at the specific point where the delta function is centered. Essentially, it's like using the delta function to 'sample' the value of another function at a certain location. This property is crucial in applications such as civil engineering, where we often deal with point loads or other concentrated effects that need to be considered at specific points.
Examples & Analogies
Imagine you're a teacher using a laser pointer to indicate a particular student in a classroom filled with many students. When you point the laser to a specific student, their attention is drawn, and they are singled out from the rest. Similarly, the Dirac delta function, when integrated, 'points' to a specific value of a function, isolating it for evaluation.
Key Concepts
-
Sifting Property: Enables extraction of function values at specific points during integration.
-
Point Loads: The application of loads at specific points modeled effectively using the delta function.
Examples & Applications
Using the delta function to model a point load on a structure allows engineers to simplify differential equations in structural analysis.
Evaluating how a pulse load impacts a dynamic system can be efficiently analyzed through the sifting property.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
A delta's peak, the values speak, at point a, their truth we seek.
Stories
Imagine a librarian who only finds and highlights the best book at each location on the shelves; that's what the delta function does when it evaluates a function!
Memory Tools
D.E.L.T.A – Delta Extracts a Location's True Answer.
Acronyms
SIFT – Sifting Integral for Function's Truth at a specific point.
Flash Cards
Glossary
- Dirac Delta Function
A mathematical function defined such that it is zero everywhere except at zero, where its integral over the entire real line is equal to one.
- Sifting Property
A property of the Dirac delta function that allows the extraction of the value of a function at a specific point through integration.
Reference links
Supplementary resources to enhance your learning experience.
