Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Laplace Transform
Unlock Audio Lesson
Today, we'll discuss the Laplace transform, particularly in relation to the Dirac delta function. Can anyone tell me why the Laplace transform is important in engineering?
It helps in solving differential equations?
Exactly! The Laplace transform is very useful in converting differential equations into algebraic equations. Now, let's link this with the Dirac delta function. What do you know about it?
It models point loads, right?
Correct! The Dirac delta function can model idealized point effects. Now, remember this, the Laplace transform of the delta function is key in dynamics.
Transform of the Dirac Delta Function
Unlock Audio Lesson
Let's focus on the specific transformation we discussed. Can anyone tell me what L{δ(t−a)} equals?
It's e^(-as) if a is greater than or equal to zero!
Great job! This is crucial as it indicates how the delta function behaves at different times. This is particularly useful when modeling sudden forces.
Can you give an example of that?
Sure! Imagine an impulse from a falling object. This transformation helps us analyze the system's response in terms of displacement or stress.
Applications of the Transform
Unlock Audio Lesson
Now, let's look into applications. How can we use the Laplace transform of the Dirac delta function in dynamic analysis?
It could help us model things like sudden impacts or loads on a structure.
Precisely! This allows us to simplify complex models of structural behavior. Any other examples?
What about a mechanical load switch?
Exactly! Switching on a mechanical load can be modeled using this property. Let’s summarize our key points: Laplace transform provides mathematical simplicity and helps model instantaneous effects.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section covers the Laplace transform of the Dirac delta function, presenting it as L{δ(t−a)}=e^(-as) for a≥0. It illustrates the significance of this property in civil engineering contexts, especially in dynamic analysis involving instantaneous loads or forces.
Detailed
The Laplace transform is a crucial tool in solving time-dependent differential equations in civil engineering. This section elaborates on how the Dirac delta function transforms under Laplace operation, specifically L{δ(t−a)}=e^(-as) for a≥0. This result is integral to modeling instantaneous effects like impulses from falling objects, mechanical load switches, or sudden impacts in structures. The Dirac delta function's behavior under the Laplace transformation allows engineers to simplify complex dynamic problems and derive solutions for systems subjected to idealized point loads.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Laplace Transforms in Civil Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In civil engineering, Laplace transforms are used for solving time-dependent differential equations.
Detailed Explanation
This chunk introduces the context of Laplace transforms specifically within the field of civil engineering. A Laplace transform is a mathematical tool that changes a function of time into a function of a complex variable, typically to make solving differential equations easier. Engineers often encounter time-dependent problems when designing or analyzing structures, and the Laplace transform helps convert these problems into a more manageable algebraic form.
Examples & Analogies
Consider a civil engineer designing a bridge. They need to analyze how the bridge will respond over time to various forces like traffic loads or wind. By using Laplace transforms, they can convert their time-based equations into simpler algebraic equations, making it easier to predict the bridge's behavior without complex calculations in time domain.
Laplace Transform of the Dirac Delta Function
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Laplace transform of the delta function is: L{δ(t−a)}=e−as, a≥0.
Detailed Explanation
This segment specifies how the Dirac delta function is transformed under the Laplace transform. Specifically, when the delta function is shifted to a point 'a', its transform becomes an exponential function, e^(-as). This result is particularly powerful because it shows that the delta function, which models an instantaneous impulse, translates to an exponential decay in the Laplace domain, reflecting the instantaneous action of a force applied at time 'a'.
Examples & Analogies
Imagine a scenario where a heavy object falls and strikes a bridge at a specific moment. The impact can be modeled using the Dirac delta function to represent the sudden force applied. When using Laplace transforms, this instantaneous force becomes an exponential decay function. This allows engineers to analyze the subsequent effects of that force on the bridge over time, facilitating their understanding of the bridge's response.
Applications of Laplace Transform in Dynamic Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
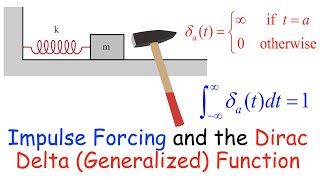
This property allows the modeling of instantaneous forcing terms in dynamic analysis of civil systems, such as: • An impulse from a falling object on a structure, • Switching on a mechanical load, • Sudden impact or blast effects.
Detailed Explanation
In this chunk, the utility of the Laplace transform of the delta function in dynamic analysis is discussed. Because the transform captures the essence of an instantaneous force, it is particularly useful for modeling various scenarios where forces are applied suddenly in civil engineering, such as impacts from falling objects, mechanical loading switches, or explosive forces. The ability to mathematically represent these events enables engineers to simulate and predict system behaviors accurately.
Examples & Analogies
Think of dynamiting a section of a road to clear the way for construction. Such a blast exerts a sudden force on the surrounding structures. By using the Laplace transform of the delta function, engineers can model the effects of this blast on nearby buildings, allowing them to assess potential damage before performing the actual operation.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Laplace Transform of δ(t-a): e^(-as) for a ≥ 0
-
Modeling instantaneous forces in civil engineering
-
Use in dynamic analysis
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Modeling an impulse from a falling object on a structure.
-
Using the Laplace transform to analyze sudden mechanical load switching.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
If forces strike in a flash, the delta shows their dash.
📖 Fascinating Stories
-
Imagine a ball dropped from a height, the moment it hits is modeled tight, that's where the delta shines so bright.
🧠 Other Memory Gems
-
D for Dirac, I for Instantaneous effect, E for e^(-as).
🎯 Super Acronyms
DIP
- Delta
- Instantaneous
- Pulse.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Laplace Transform
Definition:
A mathematical operation that transforms a time-domain function into a complex frequency-domain representation.
-
Term: Dirac Delta Function
Definition:
A generalized function used to model point sources or instantaneous effects.
-
Term: Instantaneous Force
Definition:
A force that is applied for a very short duration or instantaneously.
-
Term: Dynamic Analysis
Definition:
The study of structures or systems that change over time, typically in response to loads.