Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Dirac Delta Function
Unlock Audio Lesson
Today, we're exploring the Dirac delta function, a tool that may not be a function in the classical sense but is critical in engineering. Can anyone tell me what they understand about point loads?
Point loads are loads that are applied at a specific point on a structure.
Exactly! The Dirac delta function is essential in modeling these point loads. It has a unique property: it is zero everywhere except at the origin, where it is infinite. This allows it to mathematically represent a concentrated effect.
But how can something be zero yet infinite at the same time?
Great question! Think of it as having a total 'magnitude' of 1 when integrated across the real line, despite being infinitely peaked at one point. This is what makes it so useful.
So it's like a mathematical abstraction for completely concentrated forces?
Yes, very well put! This function is used extensively in civil engineering applications, which we'll dive into next.
What about its practical uses?
We'll cover those in detail shortly. To remember its properties, think of the acronym 'ZIN' – Zero everywhere except the origin, Infinite at the origin, and Neat integration to 1. Let's keep building on this understanding.
Properties of the Dirac Delta Function
Unlock Audio Lesson
Now that we know about the Dirac delta function, let's discuss some of its specific properties. Can anyone explain why the sifting property is important?
Isn't it used to pick values from other functions? Like if you have f(x) and multiply it by δ(x-a), you can get f(a)?
Exactly! The sifting property allows us to evaluate f at a specific point, which simplifies many complex equations. Can anyone think of a scenario where we might need this?
In structural analysis, when assessing how a point load affects a beam?
Right! We will use it to solve differential equations concerning deflection due to point loads. Remember to visualize δ(x) as a sharp spike at x = a, concentrating all its effect there.
And what about scaling and shifting properties? Those sound interesting too.
Good catch! The scaling property maintains the area under the curve, and shifting just relocates the spike. Remember these features when using delta functions in applications.
Applications in Civil Engineering
Unlock Audio Lesson
Let's move on to practical applications of the Dirac delta function in civil engineering. How might we use it in structural analysis?
Maybe to model concentrated loads on beams?
Absolutely! For instance, if we have a load P at position x = a on a beam, we might express the distributed load as q(x) = P * δ(x-a). What's the benefit of doing this?
It simplifies the equation we need to solve for deflection, right?
Exactly! It leads to simpler forms of equations to analyze the system’s response. Can someone describe an example using impulsive forces?
Like modeling a sudden impact or force in dynamics?
Precisely! This is how structures respond to dynamic loads, such as during an earthquake or blast. Keep thinking about real-life applications; they help solidify our understanding.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section introduces the Dirac delta function, defining its properties, explaining its sifting property, and discussing its applications in civil engineering, physics, and beyond. It emphasizes how it serves as a generalized function useful for simplifying complex problems involving impulses or point loads.
Detailed
Dirac Delta Function
The Dirac delta function, denoted by δ(x), is a mathematical construct employed primarily in fields such as engineering and physics for modeling point loads, impulses, or concentrated effects. While it is not a function in the traditional sense, it possesses distinct properties that facilitate the analysis of systems described by differential equations, particularly in civil engineering contexts.
Key Properties:
- Zero everywhere except at the origin: δ(x) is 0 for x ≠ 0.
- Infinite at the origin: δ(0) is considered to be infinite.
- Integral equals one: The integral over the real line is equal to one.
Heuristic Interpretation:
The function can be approximated by sequences of functions that become increasingly narrow and tall while maintaining a constant area under the curve of 1. Common approximations include rectangular and Gaussian functions.
Application of Sifting Property:
The sifting property allows users to extract function values at specific points, crucial for evaluating the influence of point loads in structural engineering. This section also explores the generalized treatment of the Dirac delta function, showcasing its applications in various engineering scenarios such as structural dynamics, fluid mechanics, and finite element analysis.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Dirac Delta Function
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Dirac delta function, though not a function in the classical sense, is a powerful mathematical tool widely used in engineering, physics, and particularly in civil engineering applications involving differential equations, structural analysis, and signal processing. It is employed to model idealized point loads, impulses, or concentrated effects, enabling the formulation and solution of problems involving such phenomena. This chapter delves into the definition, properties, and applications of the Dirac delta function, providing a rigorous understanding tailored for civil engineering contexts.
Detailed Explanation
The Dirac delta function is not a traditional function like those you may have encountered; instead, it is referred to as a 'generalized function' or a 'distribution.' This means that it cannot be defined simply by a formula but has specific properties that make it extremely useful in various fields, especially civil engineering. Essentially, this function helps in modeling scenarios where loads or effects are concentrated at a single point, allowing engineers to formulate and solve complex problems efficiently.
Examples & Analogies
Imagine dropping a small pebble into a still pond. The point where the pebble hits the water is like a point load. However, the ripples that spread out represent the effect of that load on the surrounding water. The Dirac delta function acts like the pebble: it helps engineers identify the precise impact of concentrated forces or moments in their analyses, without having to deal with complex distributions.
Concept and Informal Definition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Dirac delta function, denoted by δ(x), is not a conventional function but a generalized function or distribution. It is defined informally by the following properties:
• Zero everywhere except at the origin:
δ(x) = 0 for x ≠ 0
• Infinite at the origin:
δ(0) = ∞
• Integral over the real line equals one:
∫_{-∞}^{∞} δ(x) dx = 1
These properties make δ(x) useful for modeling idealized point effects.
Detailed Explanation
The Dirac delta function has three key properties that define it:
1. Zero everywhere except at the origin: This means that the function doesn't have any value, or effect, for any point other than zero.
2. Infinite at the origin: At the point where x equals zero, the function assumes an infinite value, which is not possible for regular functions but is meaningful in the distribution context.
3. Integral over the real line equals one: If you were to integrate the Dirac delta function over the entire real line, the area under the curve would equal one. This represents the total accumulated effect of the delta function as a point load, further emphasizing its role in modeling concentrated loads.
Examples & Analogies
Think of a very sharp spike—it's like a needle that has a very narrow tip but is infinitely tall at that tip. When you put that spike on a surface, it exerts a significant force at that very point, but nowhere else around it. The Dirac delta function captures this concept by being 'zero' everywhere except at the point of interest.
Heuristic Interpretation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Dirac delta function can be thought of as the limit of a sequence of functions that become increasingly narrow and tall, while keeping the area under the curve constant at 1. Some common approximations include:
12.2.1 Rectangular Approximation
δ(x) = { 1, |x| < ϵ; ϵ² as ϵ→0; 0, otherwise }
12.2.2 Gaussian Approximation
δ(x) = { (1/(√(ϵπ))) e^{-x²/ϵ} as ϵ→0 }
These are not the delta function itself but converge to it in the sense of distributions.
Detailed Explanation
To understand the Dirac delta function, you can think of it as an idealized version of a sequence of shapes that get progressively sharper while maintaining a constant area of 1. The rectangular approximation represents this with bars that get thinner (ϵ approaching 0) and taller. Similarly, a Gaussian approximation shows how a bell curve flattens and narrows, focusing its area at the center. While these approximations aren't perfect representations of the delta function, they help visualize how it behaves mathematically.
Examples & Analogies
Consider a concert where the singer's microphone captures the sound. If the singer holds the microphone very close to their mouth (similar to the Dirac delta function), the sound from that one point is much louder than sounds from other distances. As you gradually pull the microphone away, the sound becomes quieter and diffuses over an area, echoing the idea of approximations creating a broader effect while focusing on the single note at the center.
Sifting Property
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
One of the most important properties of the Dirac delta function is its sifting or sampling property:
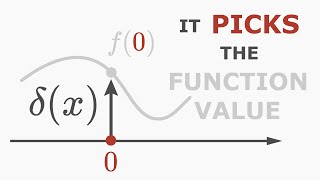
∫_{-∞}^{∞} f(x)δ(x−a) dx = f(a)
This means δ(x−a) 'picks out' the value of f(x) at x = a. This is useful in civil engineering when evaluating the effect of a point load or impulse at a specific location.
Detailed Explanation
The sifting property is crucial for applications involving the Dirac delta function. It states that when you integrate a function f(x) multiplied by δ(x - a), you get the value of f(x) at x equal to a. Essentially, the delta function acts like a spotlight that highlights a specific point, allowing engineers to evaluate forces, effects, or responses precisely where they occur. This property simplifies the analysis of systems affected by point loads or impulses.
Examples & Analogies
Imagine you're at a library and your friend is looking for a specific book in a vast collection. If your friend uses a powerful magnifying glass (analogous to the Dirac delta function), they can easily find that specific book without getting distracted by all the surrounding books. Similarly, the sifting property allows engineers to hone in on specific values when analyzing effects in structural systems.
Properties of Dirac Delta Function
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
12.4.1 Even Function
δ(−x) = δ(x)
12.4.2 Scaling Property
δ(ax) = (1/|a|) δ(x), a ∈ R, a ≠ 0
12.4.3 Shifting Property
δ(x−a): concentrated at x=a
12.4.4 Multiplication by a Function
f(x)δ(x−a) = f(a)δ(x−a)
12.4.5 Integration Involving Delta Function
∫_a^b f(x)δ(x−c) dx = { f(c), if a < c < b; 0, otherwise }
Detailed Explanation
The Dirac delta function has several important properties that make it versatile in applications:
- Even Function: This means it has symmetry, so δ(−x) is equal to δ(x).
- Scaling Property: If you scale the argument, the function adjusts its height accordingly while keeping its integral constant.
- Shifting Property: When you shift the argument, the peak of the delta function moves, allowing you to model point loads at any specified location.
- Multiplication by a Function: This property states that when multiplying a function by the delta function, it evaluates the function at the peak of the delta function.
- Integration Involving Delta Function: This shows how the delta function behaves when integrated, focusing on specific points that are part of the limits of integration. These properties simplify numerous analyses, especially in engineering contexts.
Examples & Analogies
Think of the Dirac delta function as a highly adaptable spotlight that can change its position and width based on the context. Whether it’s shining just on a specific point (shifting property) or adjusting its brightness (scaling property), it makes abstract concepts tangible. When multiple lights (functions) converge at one point (with multiplication), the spotlight ensures only the pertinent information is highlighted during a performance (integration).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Dirac Delta Function: A fundamental tool for modeling point loads and impulses.
-
Sifting Property: Key property allowing the extraction of values from functions.
-
Applications: Significant in civil engineering for structural analysis involving point loads.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Modeling a point load on a beam as a function q(x) = P * δ(x-a) simplifies solving differential equations for deflection.
-
In dynamics, applying an impulsive force F at a specific time can be represented as F(t) = F₀ * δ(t-t₀).
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
The Dirac delta, tall and steep, models loads that are not deep.
📖 Fascinating Stories
-
Imagine a spike at a point, representing a force acting at that exact location. This spike captures the whole effect of the point load.
🧠 Other Memory Gems
-
C.U.R.V.E. – Concentrated (point effect), Unique integral (equals 1), Really sharp (spike behavior), Values isolate (sifting), Everywhere else zero.
🎯 Super Acronyms
ZIN – Zero outside, Infinite at point, Neat integration to 1.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Dirac Delta Function
Definition:
A mathematical function that models idealized point loads, impulses, or concentrated effects.
-
Term: Sifting Property
Definition:
The property of the Dirac delta function that allows it to extract values from other functions.
-
Term: Point Load
Definition:
A load applied at a specific point on a structure.
-
Term: Impulse
Definition:
A sudden force applied over a brief duration of time.