Even Function
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Even Function Property
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we are going to explore an important property of the Dirac delta function, which is that it is classified as an even function. Can anyone tell me what it means for a function to be even?

Isn't it something about symmetry? Like if you fold the graph along the y-axis?

Exactly! An even function is symmetric about the y-axis. This means that for any input x, the output is the same for both x and -x. For the Dirac delta function, we have the property δ(-x) = δ(x).

So, are there practical applications for this symmetry in engineering?

Great question! This property is particularly useful in modeling symmetric distributions or point loads in civil engineering. When analyzing systems, we can simplify calculations using this evenness.

Does that mean it helps in integration processes?

Precisely! When integrating an even function over symmetric limits, you can reduce your calculations significantly. Remember this concept as we proceed in our studies.
Application of Even Functions in Engineering
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s dive into how the even property of the Dirac delta function helps us in practical scenarios. Can anyone think of an example?

How about using it in structural analysis, like in beams?

That's a perfect example! When calculating the effects of a point load on a beam, the symmetry of the even function allows for simplified equations and solutions. It makes things much easier.

What about other areas like signal processing?

Yes! In signal processing, the symmetry characteristics assist in determining signal distributions and responses. The evenness can help identify issues such as noise more efficiently.

Could you explain how we would apply it during calculations?

Certainly! When integrating an even function, if you know the value at x, you automatically know the value at -x. This simplifies your calculations significantly, especially when dealing with limits.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore the property of the Dirac delta function, highlighting its classification as an even function. This characteristic signifies that the value of the function at negative inputs is equal to its value at positive inputs, which is vital for its application in engineering and physics.
Detailed
Detailed Explanation of Even Function
The Dirac delta function, denoted as δ(x), possesses unique characteristics that make it highly useful in various scientific and engineering fields. One of these properties is that the delta function is classified as an even function, which can be mathematically expressed as:
$$ δ(-x) = δ(x) $$
This property indicates that the Dirac delta function maintains its value regardless of the sign of its input; thus, it is symmetric about the y-axis.
Significance
This evenness is particularly crucial when analyzing systems involving symmetric constructs, such as point loads in civil engineering. Being an even function, the Dirac delta function simplifies many operations in mathematical modeling, including integrals and derivatives, allowing for elegant solutions in structural analysis and signal processing.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Even Function Property
Chapter 1 of 1
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
δ(−x)=δ(x)
Detailed Explanation
An even function is defined by the property that it is symmetric with respect to the y-axis. In the context of the Dirac delta function, the property δ(−x)=δ(x) means that the value of the Dirac delta function at a negative input is the same as that at its positive counterpart. This indicates its symmetry, which is crucial for many applications in physics and engineering.
Examples & Analogies
Imagine a perfectly balanced seesaw. If a weight is placed on one side, the seesaw tips to one side, but if you were to place an equal weight on the opposite side, the seesaw would balance out again. In this analogy, the Dirac delta function behaves like those weights: it acts the same at positive and negative inputs, maintaining a balance in calculations.
Key Concepts
-
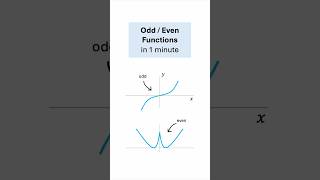
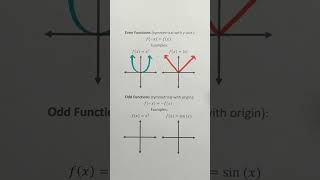
Even Function: A function f(x) is called even if f(-x) = f(x). This property implies symmetry about the y-axis.
-
Dirac Delta Function: A mathematical construct that is used for modeling point loads or impulses in engineering.
Examples & Applications
The Dirac delta function δ(x) = δ(-x) illustrates the symmetry property essential in many physical applications.
In structural engineering, when calculating the deflection of a beam under a symmetrical load, the Dirac delta function can simplify the analysis.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Even and odd, in math they play; symmetry is what keeps them at bay.
Stories
Imagine a bridge where cars drive equally from both sides, showcasing perfect symmetry, just like even functions.
Memory Tools
EAVE (Even functions Are Very Exact) to remember the properties of even functions.
Acronyms
EFS (Even Function Symmetry) can help recall the essence of even functions.
Flash Cards
Glossary
- Even Function
A function that satisfies the condition f(-x) = f(x) for all x, meaning it is symmetric about the y-axis.
- Dirac Delta Function
A distribution that is zero everywhere except at the origin, where it is infinite, and whose integral over the entire real line is equal to one.
Reference links
Supplementary resources to enhance your learning experience.
