Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Dirac Delta as a Distribution
Unlock Audio Lesson
Today, we will explore the concept of the Dirac delta function as a distribution. Who can tell me what a distribution is?
Is it a generalized function that can take different forms depending on the context?
Exactly! Distributions allow us to work with functions that are not strictly functions in the classical sense. The Dirac delta, δ(x), is a prime example. It interacts with other functions—what do you think that means?
Does it mean that it can 'pick' values from those functions?
Very well put! This 'picking' action is often referred to as the sifting property. Now, let’s define the interaction: it's expressed as ⟨δ(x-a), ϕ(x)⟩ = ϕ(a). What does this notation represent?
It shows that when you apply the delta function to a test function, it evaluates that function at the point a.
Precisely! This is what allows us to integrate and differentiate generalized functions effectively.
Sifting Property and Its Significance
Unlock Audio Lesson
Now that we've established the sifting property, can someone explain why this is useful in engineering terms?
It helps us model point loads, right? Like how the delta function represents a load applied at a precise spot!
Correct! This representation is fundamental in areas such as structural analysis. Can anyone think of a specific application?
In beam theory, where we analyze the deflection under a point load!
Great example! And how do we mathematically express that?
We use q(x) = Pδ(x-a) to show that load.
Fantastic! This formulation simplifies many calculations in engineering.
Differentiating and Integrating the Dirac Delta
Unlock Audio Lesson
Let’s dive deeper: how do we differentiate the Dirac delta function?
We can define its derivative with respect to a test function as well!
Yes, exactly! And what’s the outcome when we differentiate δ(x-a)?
It results in -f'(a) when we apply it to a test function f(x).
Correct! This is particularly useful in dynamics. Can anyone give me an example of what kind of changes we might model with this?
It could represent a sudden change in velocity or force!
Excellent! You all are grasping these advanced concepts really well.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on the Dirac delta function treated as a distribution, stating that it interacts with smooth test functions through a defined operation. This approach formalizes properties such as the sifting property, allowing for differentiation and integration of generalized functions crucial in engineering applications.
Detailed
Dirac Delta as a Distribution (Advanced View)
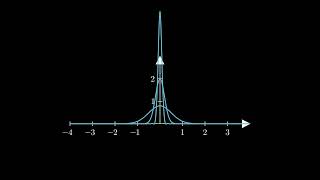
The Dirac delta function, denoted as δ(x), transcends traditional definitions of functions by acting as a distribution. In this context, it interacts with test functions, which are typically smooth (infinitely differentiable) and ensure that operations involving δ(x) yield meaningful mathematical results.
This section presents the formalization of the sifting property:
$$\langle \delta(x-a), \phi(x) \rangle = \phi(a)$$
This states that when the delta function δ(x-a) is applied to a test function ϕ(x), it evaluates ϕ at the point a, thus “sifting” through the function. This elegant representation is not merely theoretical; it allows for operations like differentiation and integration of generalized functions, cultivating a comprehensive understanding essential for its applications in fields such as civil engineering. By treating the Dirac delta function as a distribution, we enable precise modeling of phenomena such as point loads, impulses, and other concentrated effects, which are integral considerations in engineering analyses.
Youtube Videos
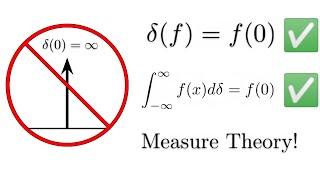
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Dirac Delta as a Distribution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To handle the delta function rigorously, it is treated as a distribution that acts on test functions:
Detailed Explanation
The Dirac delta function, denoted as δ(x), is not treated like ordinary functions due to its unique properties. Instead, it is defined in the realm of distributions. This means that it interacts with other functions in a specific way, notably with 'test functions' — smooth and well-behaved functions that are easy to work with in mathematical analysis. By treating the delta function as a distribution, we gain a framework for using it in calculus and other mathematical operations.
Examples & Analogies
Think of test functions like the instruments in an orchestra. Each instrument (test function) is essential for producing music (results), and the delta function is like the conductor that directs which instrument should play when, highlighting specific notes in a piece (function evaluation at a point). Just as the conductor uses the instruments to create beautiful music, we use test functions to interact with the delta function and extract useful information.
Sifting Property Formalization
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let ϕ(x) be a smooth test function. Then, ⟨δ(x−a),ϕ(x)⟩=ϕ(a)
Detailed Explanation
The notation ⟨δ(x−a),ϕ(x)⟩ signifies the action of the delta function δ located at point 'a' on the test function ϕ. Essentially, when you apply (or 'evaluate') the delta function on a test function, it retrieves the value of that function specifically at point 'a'. This behavior encapsulates the sifting property of the delta function, which states that it can 'pick out' the value of functions at specific points.
Examples & Analogies
Consider a fisherman casting a net. The test function ϕ(x) represents fish in a pond, while the delta function at point 'a' is like a spotlight shining on one spot in the water. When the fisherman shines his spotlight (the delta function) over the pond (the test function), he only sees the fish that are right under the beam at that specific point. This is how the delta function helps gather crucial values from continuous functions.
Differentiation and Integration of Generalized Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This formalizes the sifting property and allows differentiation and integration of generalized functions.
Detailed Explanation
By treating the Dirac delta function as a distribution, we extend traditional calculus concepts such as differentiation and integration to include generalized sequences of functions. For example, differentiating a delta function involves the concept that it can represent 'sudden changes' in adjacent test functions. Thus, it allows more complex analyses in physics and engineering where sudden impulses or load conditions are modeled.
Examples & Analogies
Imagine a switch that is turned on instantly and affects a light (test function) in a room. When the switch flips (representing the delta function), the light does not gradually start shining; it turns on immediately. Differentiation in this context helps us understand how quickly the light changes from off to on, akin to analyzing how point loads or impulses suddenly affect structures.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Dirac Delta Function: A generalized function used to model point sources.
-
Distributions: Tools for working with non-standard functions through formal definitions.
-
Differentiation of Dirac Delta: Enables mathematical manipulation for modeling dynamic changes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using the Dirac delta function to model an instantaneous point load in beam analysis.
-
Representing sudden changes in fluid dynamics using the derivative of the Dirac delta function.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To find the value, just sift right through, δ picks what's true at a point for you!
📖 Fascinating Stories
-
Imagine a scientist uses a magic sieve that only allows one grain at a time. This sieve is like the Dirac delta, which lets through only the value at a specific point.
🧠 Other Memory Gems
-
When thinking of the sifting property, remember 'D' for delta, 'S' for sifting: DS – it 'Sifts' the value.
🎯 Super Acronyms
SD = 'Sift and Determine' – representing how the Dirac delta function interacts with other functions.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Distribution
Definition:
A mathematical construct that generalizes functions, allowing for operations like differentiation and integration on non-standard functions.
-
Term: Sifting Property
Definition:
A fundamental property of the Dirac delta function where it picks the value of a function at a specific point.
-
Term: Test Function
Definition:
A smooth and well-behaved function that is used to interact with distributions.