Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Representation of Discontinuous Functions
Unlock Audio Lesson
Today we're going to explore how we can represent discontinuous functions using the Dirac delta function. To start, what is a discontinuous function?
Isn't that a function that doesn't have a well-defined value at some points?
Exactly! A common example would be a step function. Now, can anyone think of a situation where we might see a discontinuity in real-life applications?
How about in structural engineering, like when there’s a sudden change in shear force in a beam?
Great example, Student_2! We can use the Dirac delta function to model that jump mathematically. Let's look at the formula.
Mathematical Representation of Discontinuities
Unlock Audio Lesson
The representation of a discontinuous function can be expressed as: f′(x) = regular derivative + [f(a+) - f(a−)]δ(x − a). Student_3, can you explain what the terms in this formula mean?
I think f(a+) and f(a−) refer to the values of the function just after and just before the point of discontinuity, right?
Exactly! The delta function models the effect of this jump in the function value. Can anyone think of another example that might illustrate this concept?
Perfect! Such modeling is crucial in fluid mechanics and hydrology.
Applications of Discontinuous Functions in Engineering
Unlock Audio Lesson
Now, let's talk about how this representation is applied in engineering. Why do you think it's useful for our field, Student_1?
Because it simplifies the analysis of systems with sudden changes?
Exactly! By allowing us to model these abrupt changes, we can better analyze and design structures and systems. Can anyone give an example of where we might model a crack or joint in materials using this concept?
In a bridge, for instance, there might be discontinuities where materials are joined together.
Spot on! Understanding these representations helps engineers assess the integrity and safety of structures.
Review and Summary of Key Concepts
Unlock Audio Lesson
As we wrap up, can someone summarize how we can represent a discontinuous function?
We can use the formula f′(x) = regular derivative + [f(a+) - f(a−)]δ(x − a) to express sudden changes.
Excellent! What are some applications we've discussed regarding this representation?
We talked about structural changes like shear forces, pressure drops in fluids, and cracks in materials.
Great job, everyone! By using the Dirac delta function, we can simplify complex behaviors in our mathematical models.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
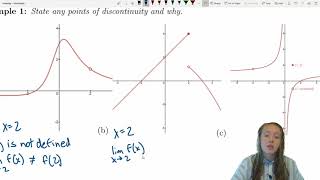
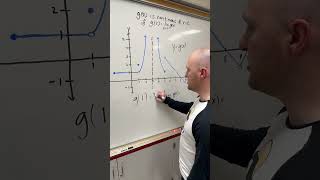
Functions that exhibit discontinuities at particular points can be expressed utilizing the Dirac delta function. This representation is crucial for describing abrupt changes in physical systems like shear forces in beams, pressure drops in fluids, and discontinuities in materials. The section outlines the mathematical expression used for these representations and their engineering significance.
Detailed
Representation of Discontinuous Functions
In the context of the Dirac delta function, this section elucidates the representation of functions that have discontinuities at specific points, typically denoted by x=a. The mathematical formulation is as follows:
f′(x) = regular derivative + [f(a+) - f(a−)]δ(x − a)
This representation is not merely theoretical; it holds significant relevance in various engineering applications. By including the Dirac delta function, one can effectively model sudden changes in system behavior, which can be observed in scenarios such as:
- A sudden jump in shear force within a beam structure.
- A sudden drop in pressure within a fluid system.
- Discontinuous transitions like cracks or joints in engineering materials.
The use of the delta function allows engineers to simplify complex models involving discontinuities into more manageable forms while still capturing essential details about the systems they are studying.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Discontinuous Functions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A function with a discontinuity at a point x=a can be expressed in terms of the delta function:
Detailed Explanation
Discontinuous functions are functions that have a sudden change in value at a specific point. For instance, a function might be smooth and continuous everywhere but suddenly jump from one value to another at a specific location. The delta function (δ) provides a mathematical way to express this sudden change. This relationship is expressed as follows: f′(x) = regular derivative + [f(a+) − f(a−)] δ(x−a). Here, 'f(a+)' represents the value of the function just after the jump and 'f(a−)' represents the value just before the jump.
Examples & Analogies
Imagine a light switch that is off but suddenly gets turned on. The function representing the light level is continuous when the light is off, but immediately changes when the switch is flipped, causing a 'jump' in brightness. The delta function captures the concept of how abrupt this change is at the moment the switch is activated.
Applications of Delta Function for Discontinuous Changes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This concept is used to describe sudden changes in system behavior, such as:
• A sudden jump in shear force in a beam,
• A pressure drop in a fluid system,
• A crack or joint in materials.
Detailed Explanation
The delta function's ability to model discontinuities has several applications in engineering. These include sudden changes in shear force within beams, where forces can change abruptly due to loads or supports. Another example is a pressure drop in a fluid system, where an instant change can occur at a certain point, like when a valve opens or closes. Additionally, physical structures may experience cracks or joints that create discontinuities, which can be mathematically modeled using delta functions to analyze stresses or strains experienced by the material.
Examples & Analogies
Consider a seesaw at the playground. When a heavy child jumps on one end, there might be a sudden shift in the angle and tension along different parts of the seesaw; this abrupt change in force can be modeled as a discontinuity. Similarly, if there’s a joint in a metal beam that fractures, the stress distribution immediately changes at the point of the fracture, which can be expressed with a delta function.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Representation of Functions: Functions with discontinuities can be represented using the Dirac delta function.
-
Formulation: The mathematical expression involves regular derivatives and delta functions to indicate sudden changes.
-
Engineering Relevance: This representation is particularly important in analyzing structures and dynamic systems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Modeling a sudden jump in shear force in a beam with the Dirac delta function.
-
Describing a pressure drop in a fluid system through its mathematical representation using discontinuous functions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When forces suddenly change in a beam, the delta function reflects the scene.
📖 Fascinating Stories
-
Imagine an engineer working on a bridge. One day, they notice a sudden crack; using the delta function, they can model this instant change precisely.
🧠 Other Memory Gems
-
Dare to model changes: Delta function helps describe abrupt shifts.
🎯 Super Acronyms
DIC = Delta, Impulse, Change
- Key concepts when thinking of jumps in functions.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Discontinuous Function
Definition:
A function that is not continuous at a certain point, exhibiting a sudden change in value.
-
Term: Dirac Delta Function
Definition:
A mathematical construct that models an idealized point load or impulse, defined to be zero everywhere except at the origin where it is infinite, with an integral of one over the entire real line.
-
Term: Shear Force
Definition:
The force in a beam or structural member that acts perpendicular to its longitudinal axis.
-
Term: Pressure Drop
Definition:
A reduction in pressure between two points in a fluid system.
-
Term: Jump Discontinuity
Definition:
A type of discontinuity where the function makes a sudden leap from one value to another.