Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Integration with Delta Function
Unlock Audio Lesson
Today, we will learn about integrating functions involving the Dirac delta function. Can anyone remind me what the Dirac delta function is?
It's a generalized function that is zero everywhere except at one point!
Correct! Now, when we integrate a function multiplied by the delta function, we leverage what's known as the sifting property. How do you think that works?
Uh, does it mean we only care about the value of the function at the point where the delta function is centered?
Exactly! When integrating within defined limits, we only evaluate the function at that particular location. Let’s look at the integration formula together.
The integration is represented as \[ \int_a^b f(x) \delta(x-c) \, dx = \begin{cases} f(c) & \text{if } a < c < b \0 & \text{otherwise} \end{cases} \]. Can anyone summarize what this means?
So if c is within the limits, we just find f(c)? But if c is outside, it equals zero!
Exactly! That's the sifting property in action. Let’s remember it with the acronym 'SIFT' – Sift It Fast to find the value!
Application of Delta Function in Engineering
Unlock Audio Lesson
Now, can anyone think of a scenario in engineering where the delta function might be useful?
Maybe in structural analysis? Like when we deal with point loads?
Bingo! The delta function is often used to model point loads on structures. So, when we integrate to find reactions in beams, the delta function simplifies our calculations significantly. Who can tell me what happens if the load is placed outside our limits?
Then the integral would just be zero, since c isn't in the limits!
Correct! As we move forward, you’ll find that this property makes the Dirac delta function a powerful tool in engineering. Remember the acronym 'LOAD' for your studies – Loads Often are evaluated using the Delta function!
Real-Life Examples of Integration
Unlock Audio Lesson
Let's summarize what we’ve learned today. Why might we use the delta function in for instance, analyzing traffic loads on highways?
We could represent the moment a vehicle enters the road as an impulse with the delta function.
Exactly! And you could integrate that to determine effects on overall traffic flow. Just remember: SIFT is how to evaluate it, and LOAD is your guiding acronym for practical scenarios.
So, we’re able to make sense of complex behaviors in systems using this concept!
That’s right! Always keep in mind where the delta function helps pinpoint values in real-world applications. Great job today, everyone!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The integration involving the Dirac delta function illustrates how to compute integrals that include the delta function, simplifying the integration process through its unique sifting property. This is crucial in many applications across engineering and physics.
Detailed
In this section, we delve into the integration properties of the Dirac delta function, specifically how it operates when integrated with another function. The key formula presented is:
\[ \int_a^b f(x) \delta(x-c) \, dx = \begin{cases} f(c) & \text{if } a < c < b \, \0 & \text{otherwise} \end{cases} \]
This equation emphasizes the 'sifting property' of the delta function, allowing us to evaluate an integral effectively by confirming whether the point of interest (c) lies within the limits of integration (a and b). The practical implications of such integrals are significant in fields such as civil engineering, where point forces or impulses at specific locations are modeled mathematically.
Youtube Videos
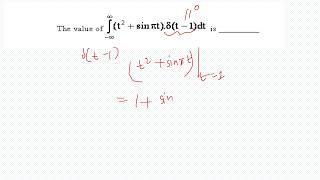
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Integration Definition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Z b (cid:26) f(c), if a<c<b
f(x)δ(x−c)dx=
0, otherwise
a
Detailed Explanation
This statement is an equation that describes how to perform integration involving the Dirac delta function, δ(x−c). The integral is evaluated over the interval from 'a' to 'b'. If the point 'c' lies strictly between 'a' and 'b' (i.e., a < c < b), the integral evaluates to the value of the function f at the point 'c'. However, if 'c' is outside this range, the integral equals zero. This property allows the delta function to 'pick out' specific values from other functions during integration.
Examples & Analogies
Think of the Dirac delta function like a spotlight on a stage. Imagine 'a' and 'b' as the edges of a stage, and 'c' as the location of a singer. When the spotlight is on the singer (c is between a and b), we see them clearly (the integral gives us f(c)), but if the spotlight is off the stage (c is outside of a and b), we don’t see anything (the integral gives us zero).
Conditions for Integration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The integral evaluates to f(c) if a < c < b, otherwise it is zero.
Detailed Explanation
In this chunk, we highlight key conditions that dictate the outcome of the integral involving the Dirac delta function. The central part of this concept is the range in which 'c' must lie for the integral to yield a non-zero result. If 'c' is sandwiched between 'a' and 'b', the integral will point to the value of the function f at 'c'. If 'c' lies anywhere outside this interval, the function does not contribute to the integral, leading to a result of zero.
Examples & Analogies
Consider a game of hide and seek. The area between 'a' and 'b' represents the safe zones where players can hide. If the 'seeker' (the integral) looks between 'a' and 'b' and finds someone (c is between a and b), they get to see who it is (the result is f(c)). However, if the hiders are outside of that safe zone, the seeker finds no one (the result is zero).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Sifting Property: The ability of the delta function to 'select' the value of a function at a specific point during integration.
-
Integration Limits: The conditions under which the delta function can effectively be integrated.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of a point load applied at x=c in beam theory modeled using Dirac delta function.
-
Impulse response of a traffic system when a vehicle enters at a specific point in time.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To find f(c), think of SIFT, where limits align, it's the integral gift.
📖 Fascinating Stories
-
Imagine a gate (the delta function) that only opens at c, letting only the values at that point through for evaluation.
🎯 Super Acronyms
SIFT - Select the Integrable by Finding Target point.
LOAD - Loads Often utilize the Delta function.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Dirac Delta Function
Definition:
A generalized function that models idealized point forces or impulses.
-
Term: Sifting Property
Definition:
The property that allows the delta function to 'select' a specific value of a function at a certain point during integration.