Derivative of the Dirac Delta Function
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Derivative of the Dirac Delta Function
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to dive into the derivative of the Dirac delta function, denoted as δ′(x). Does anyone know what the Dirac delta function is?

Isn't it a mathematical tool that represents point loads or impulses?

Exactly! δ(x) is used widely to model idealized point effects. Now, what do we think the derivative of this function might represent?

Maybe it models changes in those point effects? Like how a load suddenly affects a structure?

Yes! The derivative captures sudden changes in a system—much like how a sharp increase in force would affect a structure in engineering. Let's see how we mathematically express this.
Mathematical Definition
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Mathematically, we define δ′(x) as acting on a test function f(x) like this: $$\int_{-\infty}^{\infty} f(x) δ′(x−a) dx = -f′(a)$$. Who can tell me what this means?

It implies that the derivative δ′(x) gives us the negative value of the derivative of f(x) at point a! This means it tells us about the change of f at that point.

Well put! The action of the delta function's derivative allows us to analyze how sudden impulses affect different engineering systems.
Applications in Engineering
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's see where δ′(x) finds usefulness in engineering. Why might we care about sudden changes?

They can represent things like impulse forces that structures might experience, right?

Absolutely! In dynamics, for example, a sudden force could be modeled with δ′(t) to represent something like an impact. How important do you think understanding these concepts is?

It's crucial for designing safe structures that can withstand sudden loads!

Exactly! Understanding the implications of forces is essential for civil engineering applications.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section explains the derivative of the Dirac delta function, δ′(x), its mathematical definition, significant properties, and application in modeling phenomena like sudden impulse changes in dynamics. The section serves as a foundation for understanding how this derivative interacts with test functions in various engineering scenarios.
Detailed
Derivative of the Dirac Delta Function
The derivative of the Dirac delta function, denoted as δ′(x), is a distribution crucial for modeling instantaneous changes in physical systems. Unlike standard functions, δ′(x) is defined through its action on a test function f(x), represented mathematically as:
$$
\int_{-\infty}^{\infty} f(x) δ′(x−a) dx = -f′(a)
$$
This definition showcases how the derivative extracts information about the rate of change of the test function at the point a. This mathematical tool is particularly useful in civil engineering applications that involve sudden shifts, such as an impulse force in dynamics, where it helps characterize sudden changes in systems.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of the Derivative of Dirac Delta Function
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The derivative of the delta function δ′(x) is also a distribution, defined through its action on a test function f(x):
Z ∞
f(x)δ′(x−a)dx=−f′(a)
−∞
Detailed Explanation
In this chunk, we learn about the derivative of the Dirac delta function, which is denoted as δ′(x). Rather than behaving like a regular function, the derivative is defined in terms of how it interacts with other functions, which are referred to as test functions. To understand this definition, we look at the equation provided. The integral of the product of a test function f(x) and the derivative of the delta function δ′(x−a) is equal to the negative derivative of the test function evaluated at the point a (where the delta function is centered). This means that δ′(x) captures how rapidly a function changes at a certain point when influenced by impulse-like effects.
Examples & Analogies
Imagine you are at a concert, and someone suddenly turns up the volume very abruptly (like the Dirac delta function). Now, if we consider how your reaction changes to the music's loudness at that moment, this reaction can represent the test function f(x). The abrupt change in volume doesn't just affect the volume itself but changes how you perceive the music - this relationship illustrates the notion of the derivative of the delta function. Just like your immediate reaction is influenced by this sudden change at a specific moment, the derivative of the delta function captures how functions respond to impulse-like changes.
Applications of the Derivative of Dirac Delta Function
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This is useful in modeling sudden changes in systems (e.g., velocity jumps from an impulse in dynamics).
Detailed Explanation
The result obtained from the definition of the derivative of the Dirac delta function is particularly useful in various fields, including engineering and physics. A common application is in dynamics, where systems can experience sudden changes due to an impulse. For example, when a force is applied suddenly to a mass, it can result in an instantaneous change in velocity. The delta function derivative allows engineers to model these sudden shifts effectively, capturing the instant change without treating it as a continuous process.
Examples & Analogies
Think of a car that suddenly brakes hard. The moment the brake is applied, there's an instantaneous change in speed - from driving forward to going to a complete stop. This rapid change can be modeled using the derivative of the delta function, similar to how we would account for the impulsive force of braking. Like the derivative captures the immediate rate of change, your perception of stopping suddenly reflects this impulse, making the mathematical representation relatable to real-life experiences.
Key Concepts
-
Derivative of the Dirac Delta Function: A mathematical tool used to model sudden changes in systems.
-
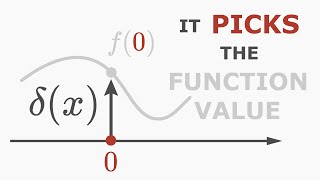
Sifting Property: The ability of the delta function to 'pick out' values from other functions at specific points.
Examples & Applications
Using δ′(x) to model a sudden impact on a structure in dynamics.
Applying the derivative in determining shear force changes in structural analysis.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Delta derivative, swift like a dive, models quick changes, helps us survive.
Stories
Imagine a bridge where a load suddenly falls. The delta derivative captures this action, predicting structural response.
Memory Tools
Remember D for Delta and D for Derivative—both describe sudden changes!
Acronyms
D2C - Derivative 2 Change; represents δ′(x) bringing sudden shifts.
Flash Cards
Glossary
- Dirac Delta Function
A generalized function representing an idealized point load or impulse.
- Distribution
A mathematical object that generalizes functions and can be used in differential equations.
- Test Function
A smooth function used to probe distributions in mathematical analysis.
- Impulse Force
A force applied over a very short duration, resulting in sudden changes in system response.
Reference links
Supplementary resources to enhance your learning experience.
