Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Even Function Property
Unlock Audio Lesson
Today, we'll discuss the first property of the Dirac delta function: it is an even function. Can anyone tell me what that means?
Does it mean it looks the same on both sides of the y-axis?
Exactly! This means δ(-x) = δ(x). It behaves symmetrically. Can someone suggest why this might be useful in applications?
It might simplify calculations if the function is symmetric!
Right! Symmetry can lead to simplified equations, especially in structural analysis.
So, remember: Even functions play a key role in making our mathematical tools more efficient.
Scaling Property
Unlock Audio Lesson
Next, let's talk about the scaling property of the Dirac delta function. Can anyone explain it?
I think it says δ(ax) = (1/|a|)δ(x) if a is not zero?
That's right! This property is crucial when we need to manipulate the delta function mathematically. Why do you think the scaling factor is 1/|a|?
So that the area under the curve remains 1, right?
Correct! Always think about the area under the curve — it’s fundamental to the concept of the Dirac delta function.
Shifting Property
Unlock Audio Lesson
Now, can someone explain the shifting property of the Dirac delta function?
It focuses on a specific point, like δ(x - a) is concentrated at x = a.
Exactly! This is pivotal in civil engineering for modeling point loads at specific locations. What might be an application of this in real life?
Would it be used to model a load on a beam?
Yes! This property helps us precisely locate where the load is applied, improving our analysis significantly.
Multiplication by a Function
Unlock Audio Lesson
Let's move to how the Dirac delta function interacts with other functions. Who can recall the formula?
I remember: f(x)δ(x - a) = f(a)δ(x - a).
Right! This shows how δ(x - a) picks out the value of f at a. What does this mean for us as engineers?
We can simplify complex functions' behavior around load points!
Exactly! It allows us to evaluate the effect of loads effectively.
Integration Involving Delta Function
Unlock Audio Lesson
Finally, let’s discuss integration involving the Dirac delta function. Can someone formulate it for us?
It's \[ \int_{a}^{b} f(x)δ(x-c)dx = f(c) \] if a < c < b.
Correct! This means we can isolate the effect of a function at a certain point. How might this be useful in real-world scenarios?
It helps determine specific responses in systems during analysis!
Very good! This property is powerful in analyzing systems and understanding their behavior under specific conditions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The properties of the Dirac delta function, including its nature as an even function, scaling, shifting, and its behavior in integration, form the foundation for applying this mathematical tool in engineering scenarios. These properties allow for modeling concentrated loads and point effects effectively.
Detailed
Properties of Dirac Delta Function
The Dirac delta function, denoted as δ(x), possesses unique properties that make it indispensable in various mathematical applications, particularly in engineering. Here are its core properties:
1. Even Function
The Dirac delta function is an even function, meaning:
- Property: δ(-x) = δ(x)
This symmetry means the function looks the same when reflected across the y-axis.
2. Scaling Property
The scaling property helps manipulate the delta function when it is subjected to a scaling transformation:
- Property: δ(ax) = (1/|a|)δ(x) for a ≠ 0
This property demonstrates how the delta function scales when its argument is multiplied by a nonzero scalar.
3. Shifting Property
This property is crucial for localized point effects in differential equations:
- Property: δ(x - a)
Here, δ(x - a) indicates the function's concentration at a specific point x = a, essential for modeling point loads or impulses at specific locations.
4. Multiplication by a Function
When multiplied by a function, this property highlights how the Dirac delta function can extract value from another function:
- Property: f(x)δ(x - a) = f(a)δ(x - a)
This property emphasizes the ability to "pick out" the function's value at the point a, useful in engineering analyses.
5. Integration Involving Delta Function
In integration, the delta function plays a pivotal role in sampling:
- Property: \[ \int_{a}^{b} f(x)δ(x - c)dx = \begin{cases} f(c), & a < c < b \ 0, & \text{otherwise} \end{cases} \]
This highlights the delta function’s capability to isolate specific values in integral form. Understanding these properties allows civil engineers to efficiently solve problems involving loads and impulses, ensuring accurate modeling of complex systems.
Youtube Videos
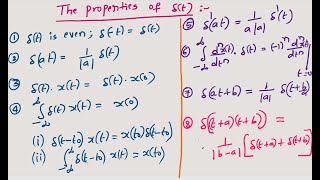
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Even Function Property
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
12.4.1 Even Function
δ(−x)=δ(x)
Detailed Explanation
The Dirac delta function exhibits a property called 'evenness', meaning it is symmetrical around the origin. This is expressed mathematically as δ(−x) = δ(x). In simpler terms, if you flip the function over the y-axis (like looking in a mirror), it looks the same. This property is important because it allows us to analyze systems where the effects are symmetrical, such as forces applied equally from both sides of a point.
Examples & Analogies
Consider a seesaw that is perfectly balanced. If you apply equal weights on both sides at equal distances from the center, the seesaw remains balanced regardless of the direction you approach from. The even function property of the delta function is similar—it doesn't matter from which side you look at it; the outcome remains unchanged.
Scaling Property
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
12.4.2 Scaling Property
δ(ax)= δ(x), a∈R,a̸=0
|a|
Detailed Explanation
The scaling property of the Dirac delta function states that if you scale its argument by a non-zero factor 'a', the result is proportional to the original function, divided by the absolute value of that scaling factor. Mathematically, this is represented as δ(ax) = (1/|a|)δ(x). This property is vital when analyzing systems with varying magnitudes of inputs, as it shows that the delta function can adapt to changes in scale while maintaining its core characteristics.
Examples & Analogies
Think about resizing an image. If you enlarge an image by a factor of two, it appears larger, but the essence of the image remains the same. The scaling property illustrates that the delta function behaves similarly; it maintains its identity regardless of whether we are examining a large or small version.
Shifting Property
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
12.4.3 Shifting Property
d δ(x−a): concentrated at x=a
Detailed Explanation
The shifting property indicates that the Dirac delta function can be moved along the x-axis without changing its fundamental nature. When we write δ(x−a), it shows that the delta function is now 'concentrated' at the point x = a. This property is especially useful in engineering when considering point loads or impulses that occur at specific locations, as it allows us to model such concentrated effects in a straightforward manner.
Examples & Analogies
Imagine a spotlight that can be directed to shine only on a specific point on a stage. Regardless of where you move the spotlight, it still focuses light at just one specific location at a time. Similarly, the shifting property of the delta function allows us to pinpoint effects to specific locations in our analyses.
Multiplication by a Function
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
12.4.4 Multiplication by a Function
f(x)δ(x−a)=f(a)δ(x−a)
Detailed Explanation
This property states that when the Dirac delta function is multiplied by another function f(x), the result extracts the value of that function at the specific point where the delta function is concentrated. Thus, f(x)δ(x−a) simplifies to f(a)δ(x−a). This feature is highly useful in resolving effects induced by forces or impulses that occur at defined points in a system, allowing for direct evaluation of the influence at that point.
Examples & Analogies
Think about using a magnifying glass to focus on a specific part of a flower. If the flower represents the entire function f(x), the magnifying glass lets you see just the details at a certain spot, which corresponds to f(a) in our multiplication property. This illustrates how the delta function helps focus on specific impacts in a broader context.
Integration Involving Delta Function
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
12.4.5 Integration Involving Delta Function
Z b (cid:26) f(c), if a<c<b
f(x)δ(x−c)dx=
0, otherwise
a
Detailed Explanation
This property outlines how to integrate the product of a function with the Dirac delta function. When integrating f(x)δ(x−c) over a range from a to b, the integral evaluates to f(c) if the point c lies within the limits of integration (a < c < b). If c is outside this range, the integral evaluates to zero. This behavior showcases the delta function's role in 'picking out' specific values of the function at pre-defined points, facilitating calculations in varied applications.
Examples & Analogies
Consider a vending machine that only dispenses a drink if you correctly input the right code. If the code (point c) is entered correctly while the machine is active (within limits a and b), you get your drink (f(c)). If the code is outside the acceptable range, nothing happens (integral equals zero). This demonstrates how the delta function only impacts results under specific conditions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Even Function: The Dirac delta function is symmetric around the y-axis.
-
Scaling Property: Describes how the delta function behaves when its input is scaled.
-
Shifting Property: Indicates where the delta function is concentrated.
-
Multiplication by a Function: Explains how it allows extraction of a specific function's value.
-
Integration: Establishes how the delta function simplifies calculating integrals.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The delta function δ(2x) would be scaled as (1/2)δ(x).
-
When you integrate h(x)δ(x-3), it will yield h(3) if 1 < 3 < 2.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Delta's a point, not a line, when zero's the place it shines.
📖 Fascinating Stories
-
Imagine a laser pointer: it 'hits' a wall precisely at one spot much like the delta function pinpoints its influence at the origin. Every force resembles the concentrated beam striking a target.
🧠 Other Memory Gems
-
Remember 'SES' for the properties: Symmetrical, Even, Scaling.
🎯 Super Acronyms
SHIM - Shifting, Integration, Multiplication help remember the key operations of the delta function.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Dirac Delta Function
Definition:
An idealized function used to model point loads or impulses, denoted as δ(x), characterized by being zero everywhere except at the origin.
-
Term: Even Function
Definition:
A function that satisfies the property f(-x) = f(x) for all x in its domain.
-
Term: Scaling Property
Definition:
Refers to the behavior of the Dirac delta function under multiplication by a non-zero scalar.
-
Term: Shifting Property
Definition:
A characteristic of the Dirac delta function whereby δ(x - a) is concentrated at the point x = a.
-
Term: Multiplication by a Function
Definition:
Refers to the property of the Dirac delta function being able to extract the value of a function at a specific point.
-
Term: Integration
Definition:
A mathematical operation that involves summing the values of a function over a range, crucial when working with Dirac delta function.