Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fourier Transforms
Unlock Audio Lesson
Today, we will discuss how the Dirac delta function is used in Fourier transforms. Can anyone tell me what they understand by Fourier transforms?
Isn't it a method to convert a signal from the time domain to the frequency domain?
Exactly! Fourier transforms help us analyze different frequency components of a signal. Now, let's connect this to the Dirac delta function. What are some properties of the delta function?
It is zero everywhere except at the origin, where it is infinite.
Excellent! And the integral over the entire real line equals one. This unique property allows us to use it effectively in system analysis. Let's dive deeper into how it appears in transforms.
Fourier Transform of the Delta Function
Unlock Audio Lesson
One key relationship is that the Fourier transform of the Dirac delta function is equal to one: F{δ(x)} = 1. Could someone explain what this means in practical terms?
It means that a delta function at the time domain represents a constant signal across all frequencies.
Correct! It establishes that the delta function does not bias frequency—to stress this, think of it as an impulse that influences every frequency equally.
So, it acts like a reference point in frequency analysis?
Precisely! Now, let's see the inverse relationship.
Inverse Transform and System Responses
Unlock Audio Lesson
The inverse transform can be expressed as Z ∞ eiωx dω = 2πδ(x). What does this mean?
It means that when we convert back, we are reconstructing the delta function from a continuous sum of waves.
Excellent observation! This illustrates how an impulse in the time domain corresponds to all frequencies combined together. In engineering, how does this help us?
It aids in analyzing how systems respond to sudden changes or impacts.
Exactly, and that's a recurring theme in civil engineering and signal processing!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The Dirac delta function plays a significant role in Fourier transforms, acting as both a function and a mathematical tool that simplifies the analysis of signals and systems. Its transformations reveal fundamental properties, such as the Fourier transform of the delta function being unity and its representation as an impulse in frequency space.
Detailed
Delta Function in Fourier Transforms
In signal processing and structural vibration analysis, the Dirac delta function, denoted as δ(x), emerges prominently within the context of Fourier transforms. The properties of delta functions become particularly useful because they allow one to represent point sources or impulses in signal analysis effectively.
12.9.1 Fourier Transform of Delta Function
The Fourier transform of a Dirac delta function is a remarkable property:
- F{δ(x)} = 1: This indicates that the delta function converts into a uniform constant across frequency space.
12.9.2 Delta Function from Inverse Transform
An important relation is derived from the inverse transform:
- Z ∞ eiωx dω = 2πδ(x)
This equation highlights how the delta function effectively describes the sum of exponential functions over all frequencies, tying back to the concept of impulse representation across the time domain. This identity sees extensive application in calculations of system responses, confirming the delta function's utility in practical engineering problems and theoretical analyses.
Youtube Videos
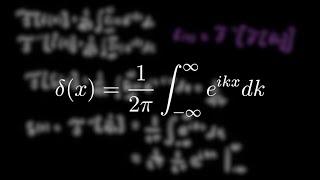
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Fourier Transform of Delta Function
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
F{δ(x)}=1, and F−1{1}=δ(x)
Detailed Explanation
This statement captures the essence of the Fourier transform of the delta function. The notation F{δ(x)}=1 indicates that when you take the Fourier transform of the delta function, you obtain a constant value of 1. Conversely, taking the inverse Fourier transform of the constant function 1 will give you the delta function, represented as F−1{1}=δ(x). This fundamental relationship illustrates how delta functions behave in the frequency domain, serving as a building block in signal processing.
Examples & Analogies
Think of the delta function as a precise moment in time, like a single clap of hands. When you capture that clap (the delta function) in an audio recording, it’s a specific sound that reverberates (transforms) into all parts of the frequency spectrum (the transform yields 1). If you want to recreate the perfect clap from the sound spectrum (inverse transform), you essentially bring back that original short, exact moment of sound—that's the delta function again.
Delta Function from Inverse Transform
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For example:
Z ∞
eiωxdω =2πδ(x)
−∞
Detailed Explanation
This equation shows the result of the inverse Fourier transform for a particular expression. When you take the integral of e^(iωx) across all frequencies (from negative to positive infinity), you arrive at 2π times the delta function δ(x). This emphasizes how the delta function is not just a singular value but serves as a bridge connecting the time and frequency domains, representing a perfect impulse at the origin. This integral is a fundamental principle in system response calculations, helping to analyze how systems respond to inputs defined in the frequency domain.
Examples & Analogies
Consider a scenario where you are throwing a stone into a calm pond. The act of throwing the stone creates ripples in the water—this is akin to an impulse at one point in time and space. Now, if you think of the ripples as a range of frequencies generated by the stone entering the water, the delta function captures that initial point of impact (the throw) which represents the strong and sudden force applied. The integral here tells us how all those ripples (the various frequencies) can be combined to effectively recreate the moment of the splash—much like we derive the delta function from the frequency spectrum.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Dirac Delta Function: A distribution that acts as an identity in linear time-invariant systems.
-
Fourier Transform: A mathematical technique to analyze signals by converting them from the time domain to the frequency domain.
-
Sifting Property: The ability of the delta function to 'pick out' values from other functions during integration.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The Fourier transform of a delta function being unity represents a constant signal over all frequencies, confirming its use in system analyses.
-
The inverse transform showing that a sum of oscillating functions results in a delta function signifies the impulse response of dynamic systems.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Delta function, oh so rare, in signals it’s everywhere!
📖 Fascinating Stories
-
Imagine a spark in a still pond, it sends ripples—just like the delta influences all frequencies in signal analysis.
🧠 Other Memory Gems
-
Remember DFP: Delta Function = Fourier Transform = Peak response at all frequencies.
🎯 Super Acronyms
DTP
- Delta
- Transform
- Peak—understanding the essential links in signal processing.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Dirac Delta Function
Definition:
A generalized function or distribution that is zero everywhere except at the origin, where it is infinite, and integrates to one.
-
Term: Fourier Transform
Definition:
A mathematical transform that decomposes a function (signal) into its constituent frequencies.
-
Term: Impulse Response
Definition:
The output of a system when it is subjected to a Dirac delta function input.