Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Fourier Transform of Delta Function
Unlock Audio Lesson
Today, we are diving into the Fourier transform of the delta function. This concept is vital for understanding signals in engineering.
What does the Fourier transform of the delta function even mean?
Great question! The Fourier transform of δ(x) results in 1. This means if you take an impulse in the time domain, it will appear constant at all frequencies in the frequency domain.
So, δ(x) essentially has information across all frequencies?
Exactly! It's like a signal that contains all frequency components equally. This leads us to look at its inverse transform.
What does the inverse transform tell us?
The inverse Fourier transform of a constant function 1 gives us the delta function itself: δ(x). This is fundamental in solving engineering problems with point loads.
Can you summarize the key points?
Of course! The Fourier transform of δ(x) is 1, and the inverse of 1 is δ(x). These results are critical for engineering analyses involving impulses.
Practical Applications of Fourier Transform in Engineering
Unlock Audio Lesson
Let’s discuss how these transforms relate to real-world applications. In structural analysis, how do we use the Fourier transform of the delta function?
It might help in analyzing responses to point loads?
Yes! When we have a concentrated load at a point, the delta function characterizes that load's effect, and its Fourier transform simplifies our calculations.
Can you give an example?
Sure! Using the delta function in dynamic analysis allows us to model impulses and understand system behavior under sudden loads. Its transform shows how these loads affect the frequency response of the system.
So, it helps predict how structures will react over time?
Exactly! By analyzing the delta function in the frequency domain, we can anticipate structural responses effectively.
Could you summarize what we learned?
Certainly! The Fourier transform of the delta function is crucial for engineering, particularly in analyzing point loads and predicting dynamic responses accurately.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section highlights the Fourier transform properties of the Dirac delta function, showing that its transform simplifies to a constant function, while its inverse indicates the delta function itself. This reveals the critical connection between the delta function and frequency domain analysis.
Detailed
Fourier Transform of Delta Function
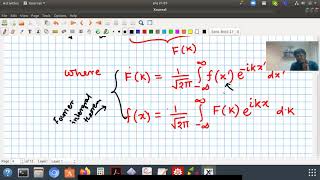
The Fourier transform is a pivotal tool in signal processing and engineering, aiding in the analysis of frequencies in a given signal. The Dirac delta function, denoted as δ(x), plays a significant role in this context. This section establishes two key identities for the delta function in the Fourier domain:
- Forward Transform: The Fourier transform of the delta function results in:
$$ F\{\delta(x)\} = 1 $$
This indicates that the frequency representation of an impulse (the delta function) is constant across all frequencies.
- Inverse Transform: Conversely, an inverse Fourier transform of a constant function gives rise to the delta function:
$$ F^{-1}\{1\} = \delta(x) $$
This relationship is crucial in various engineering applications, particularly in system response calculations, where the delta function effectively denotes instantaneous impulses or point loads.
The identities in this section elegantly underline the inherent connection between time-domain signals and their frequency-domain counterparts, thereby facilitating advanced analysis techniques in civil engineering contexts.
Youtube Videos
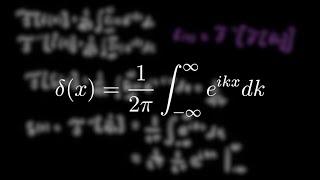
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Fourier Transform of the Delta Function
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
F{δ(x)}=1, and F−1{1}=δ(x)
Detailed Explanation
The notation F{δ(x)}=1 indicates that the Fourier transform of the delta function δ(x) results in a constant value of 1. Similarly, the inverse transform, denoted as F−1{1}=δ(x), shows that the inverse Fourier transform of a constant (1) produces the delta function. This implies that in the frequency domain, the delta function represents a constant signal across all frequencies.
Examples & Analogies
Think of the delta function as a super bright light beam shining at a single point. When we view this light in a different perspective (the Fourier transform), we see that this single point of light illuminates the whole area equally, thus representing a constant intensity over the entire space (which is why it translates to 1 in the frequency domain). When we try to reconstruct this light from its constant intensity, we find it peaks back at that same point of brightness (the delta function).
Delta Function from Inverse Transform
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For example:
Z ∞
eiωxdω =2πδ(x)
−∞
Detailed Explanation
This equation states that the integral of e^(iωx) over all frequencies (ω) yields 2π multiplied by the delta function δ(x). This implies that the delta function plays a key role in capturing all frequencies when integrated. In essence, when we consider the whole spectrum of frequencies, the outcome collapses back to a specific point in time or space (where x=0). The factor 2π is a scaling factor resultant from the properties of Fourier transforms.
Examples & Analogies
Imagine you are dropping a stone into a still pond. The sound wave created when the stone hits the water can be seen as the integral of all the waves (frequencies) produced by that impact. When we analyze these waves (like our integral), we can identify the moment of impact precisely at the spot where the stone entered the water (the delta function represents this specific event). Similarly, just like we can identify that moment with the delta function, we can reconstruct signals back to their source in signal processing.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Fourier Transform of Delta Function: The Fourier transform of δ(x) is 1, indicating it has constant frequency representation.
-
Inverse Fourier Transform: The inverse transform of the constant function 1 returns the delta function δ(x), linking time and frequency domains.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The delta function models a point load in structural engineering, simplifying calculations involving differential equations.
-
In vibration analysis, the impulse load is represented as a delta function, which helps predict the system's frequency response.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Delta in time is a point so fine, transforms to one, across all the line.
📖 Fascinating Stories
-
Imagine a landscape where every sound is constant; this is like the Fourier transform of δ(x), where every frequency has equal weight, symbolizing a perfect impulse.
🧠 Other Memory Gems
-
F1 - Function transforms to 1 shows how impulse shapes with the delta sun.
🎯 Super Acronyms
DFT
- Delta Function = 1 in Fourier Transform.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Dirac Delta Function
Definition:
A mathematical function that models an idealized point load or impulse, defined by properties such as being zero everywhere except at a specific point where it is infinite.
-
Term: Fourier Transform
Definition:
A mathematical operation that transforms a time-domain signal into its frequency components, providing insights into the signal's characteristics in the frequency domain.
-
Term: Impulse
Definition:
A sudden force or load applied over a very short time period, modeled in engineering using the delta function.