Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Differential Equations
Unlock Audio Lesson
Today, we will explore differential equations, which are equations that involve unknown functions and their derivatives. Can anyone tell me why they might be important in engineering?
I think they help in predicting how things change over time, like structures under loads.
Exactly! Differential equations allow engineers to model various physical phenomena, like fluid flow and heat conduction. Now, what do we mean by the order of a differential equation?
Is it the highest derivative in the equation?
Correct! The order is indeed the highest derivative present. And what about the degree?
It's the power of the highest derivative, right?
Precisely! Great job, everyone. Remember, understanding these definitions is the foundation for tackling more complex equations later on.
Linear Differential Equations
Unlock Audio Lesson
Let’s now look at linear differential equations. These are equations where the dependent variable and its derivatives appear only to the first power and are not multiplied together. Can someone give me an example of a first-order linear differential equation?
Is it dy/dx + P(x)y = Q(x)?
Yes! That’s a perfect example. In this equation, P(x) and Q(x) are functions of x. Now, who can remind us of the general form for second-order linear differential equations?
It's d²y/dx² + P(x)d(y)/dx + Q(x)y = R(x).
Spot on! These equations can also be classified as homogeneous or non-homogeneous. Well done, team!
Applications of Differential Equations
Unlock Audio Lesson
Let’s discuss how differential equations apply specifically in civil engineering now. What applications do you think are prevalent in this field?
We could use them for beam deflection and analyzing loads.
And fluid flow in pipelines!
Absolutely! Applications like beam deflection, fluid mechanics, and even environmental engineering are rooted in differential equations, making them essential for solving real-world problems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explores the definition of differential equations, their classification based on order and degree, and the characteristics of linear differential equations, emphasizing their significance in modeling and engineering problems.
Detailed
In this section, we delve into the definition of differential equations, which are equations involving an unknown function and its derivatives. Key concepts include 'order'—the highest derivative present in the equation—and 'degree'—the power of the highest derivative, given that the equation is polynomial in derivatives. Additionally, we define linear differential equations, where the dependent variable and its derivatives appear to the first power without being multiplied together. The examples provided illustrate both first-order and second-order linear differential equations, setting the stage for understanding their applications in civil engineering contexts.
Youtube Videos
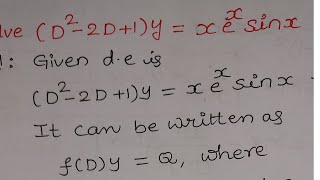
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of a Differential Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A differential equation is an equation that involves an unknown function and its derivatives.
Detailed Explanation
A differential equation is a mathematical statement that relates a function, which we usually don't know, to its rates of change (derivatives). This means that the equation has a function whose behavior we want to understand, alongside expressions that describe how this function changes. For example, if we have a function that represents the position of an object over time, its derivative would represent its velocity.
Examples & Analogies
Think of a differential equation like a recipe. Just as a recipe tells you not only what ingredients to use but also how they interact with each other to create a dish, a differential equation describes how a particular quantity (the ingredient) is interrelated with its rate of change over a certain time (how it's cooked or prepared).
Components of a Differential Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A differential equation includes an unknown function and its derivatives.
Detailed Explanation
The key components of a differential equation are the unknown function (often denoted as y or f(x)) that we want to solve for, and its derivatives, which represent the rates at which the function is changing. These derivatives provide insight into the dynamics of the function's behavior; for example, the first derivative gives us the slope of the function at any point, and higher derivatives provide information about the curvature and other properties.
Examples & Analogies
Imagine you are monitoring the growth of a plant. The height of the plant can be considered the function. The rate of growth at any moment is the first derivative (how fast it's growing at that moment), while how the rate of growth itself changes over time is the second derivative. A differential equation allows you to relate all these characteristics mathematically.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Differential Equations: Equations involving unknown functions and their derivatives.
-
Order: The highest derivative present in a differential equation.
-
Degree: The power of the highest derivative in a polynomial equation.
-
Linear Differential Equations: Differential equations where the variable and its derivatives are in the first power.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
dy/dx + 2y = e^(-x) is a first-order linear differential equation.
-
d²y/dx² + 3(dy/dx) + 2y = 0 is a second-order linear differential equation.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In every differential equation's dance, derivatives show their change in advance.
📖 Fascinating Stories
-
Imagine a bridge. As loads change, so do its forces; differential equations tell engineers how it sways and bends.
🧠 Other Memory Gems
-
O.L.D. - Order, Linear, Degree - remember the steps when drafting differential equations.
🎯 Super Acronyms
L.E.D. - Linear equations use Exponents simply in Degree; remember L.E.D. for understanding.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Differential Equation
Definition:
An equation that involves an unknown function and its derivatives.
-
Term: Order
Definition:
The highest derivative present in the equation.
-
Term: Degree
Definition:
The power of the highest derivative, provided the equation is polynomial in derivatives.
-
Term: Linear Differential Equation
Definition:
A differential equation where the dependent variable and its derivatives appear to the first power and are not multiplied together.