Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fourier Transforms
Unlock Audio Lesson
Today, we’re going to discuss Fourier Transforms. Can anyone tell me what they think the term means?
Is it about transforming signals or something similar?
Exactly! Fourier Transforms help us convert signals from the time domain to the frequency domain. This is important because it simplifies the solution of differential equations. Remember the concept of transforming; think of it like translating a complex language into something simpler to understand.
What kind of problems do these transforms help solve?
Great question! They're especially useful in heat conduction, signal processing, and structural analysis. By turning differential equations into algebraic ones, we can analyze more complex systems efficiently.
Are there specific conditions we need to remember for these transforms?
Yes! You will learn about boundary conditions later, which are essential when applying these transforms. So keep that in mind!
So it’s like changing the form of an equation to make it easier?
Exactly. It’s all about simplification and efficiency in solving engineering problems.
Applications of Fourier Transforms in Engineering
Unlock Audio Lesson
Now that we understand what Fourier Transforms are, let’s talk about where they are used in engineering.
Can we get some examples?
Certainly! In heat conduction problems, we can model how heat distributes in a material over time. Fourier Transforms help in simplifying the equations involved.
What about signal processing?
Signal processing is another key area! It analyzes the frequency components of signals, which can help in filtering and signal reconstruction.
And structural analysis?
Yes! Engineers use Fourier Transforms to analyze dynamic responses in structures, which helps in understanding vibrations and stability.
Sounds like it covers a lot of ground!
Absolutely! Understanding these applications will help you in your future engineering endeavors.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section introduces the concept of Fourier Transforms and their critical role in simplifying the solution of differential equations, particularly in engineering contexts such as heat conduction, signal processing, and structural analysis.
Detailed
Fourier Transform (Overview in Engineering Context)
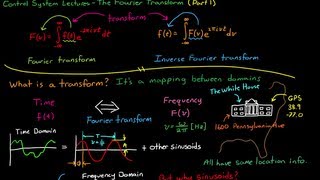
The Fourier Transform is a fundamental mathematical tool used in engineering that allows the conversion of complex differential equations into simpler algebraic equations. This process is particularly significant in scenarios involving boundary conditions, facilitating the analysis of systems in various fields such as heat conduction, signal processing, and structural analysis. By using Fourier transforms, engineers can derive solutions that are often easier to analyze and interpret, leading to more efficient design and problem-solving strategies in engineering applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Fourier Transforms
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In later chapters, you will learn about Fourier transforms used to solve differential equations with boundary conditions—useful in heat conduction, signal processing, and structural analysis.
Detailed Explanation
Fourier transforms are mathematical techniques that break down functions or signals into their constituent frequencies. In engineering contexts, particularly in solving differential equations, this method becomes handy. For example, when tackling problems related to heat conduction, engineers often deal with complex equations that describe how heat spreads through materials. Fourier transforms simplify these equations, allowing engineers to find solutions more easily.
Examples & Analogies
Imagine trying to understand a piece of music. The Fourier transform is like a tool that helps you separate the music into different notes and rhythms. Just as understanding each note can help you appreciate the full song, breaking down a complex differential equation into simpler parts through a Fourier transform allows engineers to analyze and solve it more effectively.
Transformation of Differential Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For now, understand that these tools help convert differential equations into algebraic equations, simplifying their solution.
Detailed Explanation
Differential equations describe how quantities change and are often complex and difficult to solve directly. However, by using Fourier transforms, these equations can be converted into algebraic equations, which are generally easier to handle. Algebraic equations have straightforward operations like addition, subtraction, multiplication, and division, making them significantly simpler to work with than their differential counterparts.
Examples & Analogies
Consider trying to solve a complicated puzzle. A differential equation is like having all the puzzle pieces mixed together, making it hard to see the overall picture. The Fourier transform acts like a sorting tool that organizes the pieces, helping to put them together (convert to algebraic form) and solve the puzzle (find the solution) more efficiently.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Fourier Transform: A method to convert time-domain signals into frequency-domain signals.
-
Algebraic Simplification: The process of transforming complex differential equations into simpler algebraic forms.
-
Boundary Conditions: Constraints essential for the accurate resolution of differential equations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In telecommunications, the Fourier Transform is used to analyze signal frequencies for optimal transmission.
-
In thermal engineering, Fourier Transform assists in modeling heat dissipation in multi-layered materials efficiently.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In Fourier’s land, signals take flight, from time to frequency, they shine so bright!
📖 Fascinating Stories
-
Imagine a chef using different spices (frequencies) to prepare a unique dish (signal). The Fourier Transform is like the chef's recipe, translating raw ingredients into a delicious meal.
🧠 Other Memory Gems
-
F.T. (Fourier Transform) - Find Transforms, meaning we are finding the underlying frequency in any signal.
🎯 Super Acronyms
F.T. - Frequency Translator helps you remember its purpose.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fourier Transform
Definition:
A mathematical technique that transforms a time-based signal into its frequency components.
-
Term: Algebraic Equation
Definition:
An equation that consists of numbers and variables without involving derivatives.
-
Term: Boundary Conditions
Definition:
Constraints necessary for solving differential equations that define the behavior of the system at the edges of the domain.
-
Term: Signal Processing
Definition:
The analysis, interpretation, and manipulation of signals, often using transforms like the Fourier Transform.
-
Term: Heat Conduction
Definition:
The process by which heat energy is transferred through materials.