Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
General Form of Non-Homogeneous Linear Equations
Unlock Audio Lesson
Today we're discussing non-homogeneous linear equations. They take the form: \( \frac{d^2y}{dx^2} + b \frac{dy}{dx} + cy = R(x) \). Can anyone tell me what the significance of the non-zero function, R(x), is?
It represents an external source or influence on the system.
Exactly! This external influence makes our solutions a bit more complex. Now, can someone explain what we mean by the complementary function?
It’s the solution to the homogeneous part of the equation, which is when R(x) equals zero.
Great! The complementary function captures the system's natural behavior, while the particular solution is what we’ll find for our specific R(x). Remember this as CF for complementary function!
Complete Solution
Unlock Audio Lesson
Now let's talk about the complete solution. How do we combine our complementary and particular solutions, and what's the formula?
We add them together, so \( y = y_c + y_p \).
That's correct! This formula indicates that the overall solution is a combination of the behavior dictated by the system's properties and the external influences represented by R(x).
So if we find both parts separately, we get the complete picture of our system's response.
Exactly! Always think of the CF as what the system does on its own and the PS as what happens due to external influences. This duality is crucial!
Methods for Finding Particular Solutions
Unlock Audio Lesson
Let's discuss methods to find our particular solution. Who can tell me about the Method of Undetermined Coefficients?
It's for when R(x) is a polynomial, exponential, or sinusoidal! We assume a form for y_p and solve for the coefficients.
Exactly! It simplifies our work by allowing us to guess the form of the solution. Can anyone share how you might approach R(x) if it's not suitable for this method?
In that case, we use the Variation of Parameters, right?
Correct! This method allows us to adjust the homogeneous solution to find a suitable particular solution for more complex R(x). Remember: guess, substitute, adjust!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section covers non-homogeneous linear equations, which arise in contexts where an external force or input affects the system. It details their general form, the concepts of complementary and particular solutions, and the methods used to find particular solutions such as the method of undetermined coefficients and variation of parameters.
Detailed
Non-Homogeneous Linear Equations
In this section, we delve into non-homogeneous linear differential equations, which take the form:
$$ \frac{d^2y}{dx^2} + b \frac{dy}{dx} + cy = R(x) $$
where R(x) is a non-zero function that introduces a source term into the system. The solution to these types of equations consists of two parts: the complementary function ($y_c$), which solves the associated homogeneous equation, and the particular solution ($y_p$), which provides a specific solution that accounts for R(x).
General Form
- The general structure of non-homogeneous linear equations consists of derivatives and coefficients.
- The complementary function (CF) is derived from solving the homogeneous part of the equation, while the particular solution (PS) addresses the non-homogeneous aspects introduced by R(x).
Complete Solution
The complete solution can be represented as:
$$ y = y_c + y_p $$
This highlights the necessity of both the CF and PS in determining the behavior of the system described by the differential equation.
Methods of Finding Particular Solutions
Two main methods are discussed:
- Method of Undetermined Coefficients: This method is applicable when R(x) takes a polynomial, exponential, or sinusoidal form. It requires assuming a suitable form for $y_p$ and determining the coefficients by substituting into the original equation.
- Method of Variation of Parameters: This is a more flexible approach used when R(x) does not fit the criteria for undetermined coefficients. It incorporates adapting the homogeneous solution by introducing functions that depend on the independent variable to create the particular solution.
Understanding non-homogeneous linear equations is essential in many engineering applications, as they often model systems subjected to external influences.
Youtube Videos
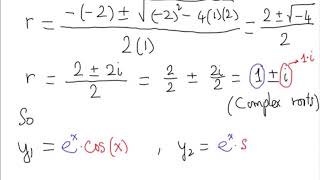
Audio Book
Dive deep into the subject with an immersive audiobook experience.
General Form of Non-Homogeneous Linear Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The general form of a non-homogeneous linear equation is:
d²y/dx² + b(dy/dx) + cy = R(x)
Detailed Explanation
Non-homogeneous linear equations are of the form where we have a linear combination of the function y and its derivatives equal to some function R(x) that is not zero. Here, d²y/dx² and dy/dx are derivatives of y, and b and c are constants. The key here is that the equation is 'non-homogeneous', meaning there is an additional term R(x) affecting the system, which can represent external forces or influences.
Examples & Analogies
Think of the equation as describing the motion of a swing being pushed. The swing's motion (y) is influenced by both its natural movement (the left side of the equation) and an external force from someone pushing it (R(x)).
Complete Solution of Non-Homogeneous Linear Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The complete solution for a non-homogeneous linear equation is written as:
y = yc + yp
where:
yc = Complementary function (solution of the homogeneous equation)
yp = Particular solution
Detailed Explanation
The complete solution consists of two parts: the complementary function (yc) and the particular solution (yp). The complementary function is the solution to the associated homogeneous equation (where R(x) = 0) and reflects the system's natural behavior. The particular solution is a specific solution that takes into account the presence of the term R(x), which could represent an external influence or force acting on the system. Therefore, to find the complete solution, you must find both components and then add them together.
Examples & Analogies
Imagine a music system. The complementary function (yc) is like the natural sound quality from the speakers when no music is playing. The particular solution (yp) is the specific song or sound being played. Together, they give you the overall audio experience, where the music (yp) complements the inherent sound quality of the system (yc).
Methods of Finding Particular Solution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
-
Method of Undetermined Coefficients
Use when R(x) is polynomial, exponential, or sinusoidal.
• Assume a suitable form for yp
• Substitute into the equation to find constants. -
Method of Variation of Parameters
Use when R(x) is not suitable for undetermined coefficients.
If the homogeneous solution is:
yc = C1y1(x) + C2y2(x)
Then the particular solution is:
yp = u1(x)y1(x) + u2(x)y2(x)
where u1, u2 are found by solving:
• u1’y1 + u2’y2 = 0
• u1’y1’ + u2’y2’ = R(x)
Detailed Explanation
To find the particular solution (yp) of a non-homogeneous linear equation, there are two main methods: 1. Method of Undetermined Coefficients: Use this method when the function R(x) is simple, such as a polynomial, exponential, or sinusoidal function. You assume a form for yp that matches the type of R(x) and find the unknown coefficients by substituting it back into the equation. 2. Method of Variation of Parameters: This method is applicable when R(x) is more complex. Here, you use an existing solution from the homogeneous equation (yc) and modify its coefficients (using functions u1 and u2) to derive the particular solution that fits with R(x). This method is a bit more involved and requires solving a system of equations to determine the new coefficients.
Examples & Analogies
Imagine trying to predict the temperature in a room (the outcome, yp) based on different sources of heat (R(x)). If the heating system's output was constant or predictable, you could model it simply (Method of Undetermined Coefficients). However, if you had varying factors affecting the temperature—like open windows or people entering—then you'd consider these factors as variables altering the existing temperature patterns (Method of Variation of Parameters).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Non-Homogeneous Linear Equations: These equations include an external force or influence, differentiating them from homogeneous equations.
-
Complementary and Particular Solutions: The complete solution to a non-homogeneous equation is the sum of its complementary and particular solutions.
-
Methods of Finding y_p: Methods such as the Undetermined Coefficients and Variation of Parameters help in finding particular solutions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For R(x) = 5, a particular solution could be y_p = C, where C is a constant value.
-
If R(x) = xe^x, then we could guess a particular solution of the form y_p = (Ax + B)e^x.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In equations complex and vast, / R(x) provides the influence cast.
📖 Fascinating Stories
-
Imagine a dam where the water is calm (CF) until a storm (R(x)) creates a rush, changing the landscape entirely.
🧠 Other Memory Gems
-
CF, PS: Complementary F and Particular S distinguish the generality from specific influence.
🎯 Super Acronyms
CP = CF + PS.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: NonHomogeneous Linear Equation
Definition:
A differential equation involving a non-zero function that incorporates additional influences on the system.
-
Term: Complementary Function (CF)
Definition:
The solution to the associated homogeneous equation when R(x) = 0.
-
Term: Particular Solution (PS)
Definition:
The specific solution of a non-homogeneous equation that accounts for the external influence R(x).