Methods of Finding Particular Solution
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Method of Undetermined Coefficients
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to delve into the Method of Undetermined Coefficients for finding particular solutions for non-homogeneous linear differential equations. Who can tell me what kind of functions we can use this method on?

I think we can use it for polynomials and exponential functions.

Excellent! We can also use it with sine and cosine functions. It's crucial to assume a form for the particular solution, denoted as yp. Can anyone suggest how to choose that form?

We match the form based on the non-homogeneous term R(x).

Exactly! We then substitute yp into the differential equation to solve for the coefficients. Remember the acronym ACR: Assume, Coefficient, and Result. This will help you recall the steps.

So, we first assume a form, then find the coefficients, and finally, we’ll have our particular solution?

Correct! Let's remember ACR as we tackle exercises. We now understand the first method well.
Method of Variation of Parameters
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's discuss the Method of Variation of Parameters. Who can explain when we use this method?

We use it when the R(x) isn't suitable for the Method of Undetermined Coefficients.

That's right! This method involves using the complementary solution, denoted as y_c. Can anyone tell me how we express the particular solution in this method?

We write y_p as u1(x)y1(x) + u2(x)y2(x), where u1 and u2 are functions of x.

Exactly! And how do we determine u1 and u2?

We solve the system of equations that incorporates y1 and y2, right?

That's true! We set up these equations, differentiate, and eventually find u1 and u2 by integrating. Remember, it's like piecing together a puzzle!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section covers two main approaches to finding particular solutions for non-homogeneous linear differential equations: the Method of Undetermined Coefficients, suitable for specific forms of R(x), and the Method of Variation of Parameters, applicable when the former method fails. Each method is described thoroughly with explanations on how to derive the solutions.
Detailed
Methods of Finding Particular Solution
This section introduces two primary methods for determining particular solutions to non-homogeneous linear differential equations.
Method of Undetermined Coefficients
- This method is applicable when the non-homogeneous term, R(x), is a polynomial, an exponential function, or sinusoidal (sine or cosine) functions.
- The process involves assuming a specific form for the particular solution, denoted as yp, which reflects the type of R(x). Following this, the assumed solution is substituted back into the differential equation to determine the coefficients. This method allows us to systematically derive the constants needed in the solution.
Method of Variation of Parameters
- This method is used when R(x) does not fit the conditions suitable for the Method of Undetermined Coefficients.
- It starts with the complementary solution, y_c, which is formed from the homogeneous part of the differential equation. The particular solution, y_p, is then expressed in terms of the complementary functions, but with variable coefficients, u1 and u2, which are functions of x rather than constants.
- To find u1 and u2, we set up a system of equations that incorporates y1 and y2, the solutions of the homogeneous equation, resulting in expressions that allow for solving u1 and u2 through integration.
These methods are foundational in solving non-homogeneous linear differential equations and have significant applications in engineering fields, particularly in analyzing complex real-world systems.
Youtube Videos



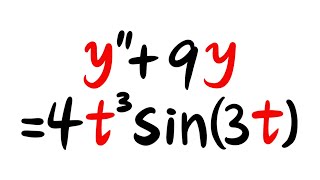






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Method of Undetermined Coefficients
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Use when R(x) is polynomial, exponential, or sinusoidal.
• Assume a suitable form for y_p
• Substitute into the equation to find constants.
Detailed Explanation
This method is specifically used for finding a particular solution when the non-homogeneous term R(x) takes the form of polynomials, exponentials, or sinusoidal functions. The first step is to 'assume' a functional form for the particular solution (y_p). This means you can guess a function that resembles R(x). Next, you substitute this assumed form into the differential equation. By doing this, you can solve for the constants in your assumed function, adjusting them so that your equation balances correctly.
Examples & Analogies
Think of this method like trying to find out how much flour and sugar you need for a new cake recipe. If you know the desired taste (R(x)), you make an educated guess about the amounts (the form of y_p) based on similar recipes. You mix them into your batter (substituting into the equation) and adjust the amounts to get the flavor just right (finding the constants).
Method of Variation of Parameters
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Use when R(x) is not suitable for undetermined coefficients.
If the homogeneous solution is:
y = C_1 y_1(x) + C_2 y_2(x)
Then particular solution is:
y_p = u_1(x)y_1(x) + u_2(x)y_2(x)
Where u_1, u_2 are found by solving:
{ u_1' y_1 + u_2' y_2 = 0
u_1' y_1 + u_2' y_2 = R(x) }
Detailed Explanation
This method is useful when the non-homogeneous term R(x) does not fit the requirements of the undetermined coefficients method. First, you start with the homogeneous solution, which is a general solution formed from two functions y_1(x) and y_2(x). For the particular solution (y_p), you express it as a combination of these two functions multiplied by new unknown functions u_1(x) and u_2(x). The next step is to set up a system of equations where u_1' and u_2' are related to the original equation, allowing you to determine the functions u_1 and u_2.
Examples & Analogies
Imagine you're trying to create a personalized workout plan that incorporates two core exercises you know work well (like push-ups and squats). However, you realize that based on your current fitness level (R(x)), you need to adjust how much you rely on each exercise (u_1 and u_2). Instead of sticking to fixed sets, you tweak your workout dynamically based on your needs (the particular solution). By analyzing how each exercise impacts your overall fitness, you can develop an effective and personalized routine.
Key Concepts
-
Method of Undetermined Coefficients: A systematic approach for finding particular solutions by assuming a form based on R(x).
-
Method of Variation of Parameters: An alternative approach for more complex non-homogeneous terms, involving variable coefficients.
Examples & Applications
Using the method of undetermined coefficients, if R(x) = e^x, assume a particular solution of the form yp = Ae^x, substitute into the equation to find A.
For a differential equation where R(x) is a polynomial, assume yp has the same polynomial degree, find the coefficients through substitution.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When undetermined coefficients you try, assume a form, give it a try!
Stories
Imagine a detective at a crime scene (R(x)). He assumes a suspect based on clues (yp form). He then investigates (substitutes back) to find out who it was (coefficients).
Memory Tools
Acronym UV for Variation of Parameters: U - Use y_c, V - Variables change to find yp.
Acronyms
UCF for Undetermined Coefficients Formula
- Use a form
- Coefficients
- Final solution.
Flash Cards
Glossary
- Particular Solution
A specific solution to a non-homogeneous linear differential equation that satisfies the differential equation and the initial/boundary conditions.
- Undetermined Coefficients
A method for finding particular solutions to certain types of differential equations by assuming a functional form and solving for unknown coefficients.
- Variation of Parameters
A method for finding particular solutions where the coefficients in the equation are allowed to vary instead of being constant, typically used when the first method isn't applicable.
- Complementary Function
The general solution of the corresponding homogeneous differential equation, denoted as y_c.
Reference links
Supplementary resources to enhance your learning experience.
